投稿日:
【高校物理】微分法とその応用【高校数学】【微分】
\(\require{color}\)
\(\require{cancel}\)
微分法については、「微分係数と導関数」で少し扱いましたが、今回は合成関数や逆関数の微分、また三角関数の微分などについて解説していきます。
微分・積分に関する記事は、こちらも参考にしてください
→微分係数と導関数
→積分法
→様々な関数
→極限
→積分法の応用
→よく使う積分の考え方と微積公式まとめ
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.導関数の復習
関数\(f(x)\)の導関数\(f'(x)\)の定義は、
\(\displaystyle{f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}}\)
上記、関数\(f(x)\)から導関数\(f'(x)\)を求めることを、”\(f(x)\)を\(x\)で微分する”といいます。
導関数は\(f'(x)\)の他にも、\(\displaystyle{y’、\frac{dy}{dx}、\frac{d}{dx}f(x)}\)のように表すこともあります。
また、\(x\)の増分を\(h\)の代わりに\(\Delta{x}\)とし、このときの\(y\)の変化量\((f(x+\Delta{x})-f(x))\)を\(\Delta{y}\)とすると、
\(\displaystyle{f'(x)=\lim_{\Delta{x}\to0}\frac{\Delta{y}}{\Delta{x}}}\)
と表すことができます。
\(\Delta\)は”デルタ”とよび、変化量を表します。
\(\Delta{x}\)は\(x\)の変化量、\(\Delta{y}\)は\(y\)の変化量という意味になります。
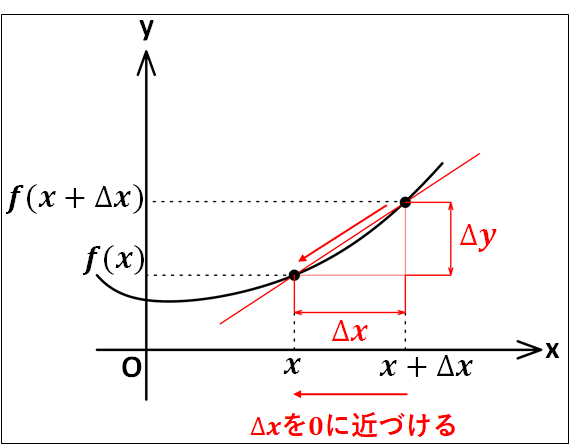
※\(x\)の変化量を\(\Delta{x}\)とすると
\(\Delta{x}=(x+h)-x=h\)
\(x\)の変化量に対する\(y\)の変化量を\(\Delta{y}\)とすると
\(\Delta{y}=f(x+\Delta{x})-f(x)\)
導関数の定義式は、
\(\displaystyle{\begin{eqnarray}f'(x)&=&\frac{dy}{dx}\\\\&=&\lim_{\Delta{x}\to0}\frac{\Delta{y}}{\Delta{x}}\\\\&=&\lim_{\Delta{x}\to0}\frac{f(x+\Delta{x})-f(x)}{\Delta{x}}\end{eqnarray}}\)
となる。
2.導関数の公式
2-1.積の微分公式
導関数の公式には以下のようなものがあります。
関数\(f(x)、g(x)\)がともに微分可能であるとき、
\(\displaystyle{\left.\begin{eqnarray}&&{kf(x)}’=kf'(x)\\\\&&{f(x)+g(x)}’=f'(x)+g'(x)\\\\&&{f(x)-g(x)}’=f'(x)-g'(x)\end{eqnarray}\right\}\bf{復習※1}}\)
\(\displaystyle{\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)\cdots①}\)
(※1)については、「微分係数と導関数」で扱いました。
\(①\)の公式を、\(\textcolor{red}{\bf{“積の微分公式”}}\)といいます。
\(\underline{\bf{①について}}\)
これを導関数の定義から証明します。
定義から、
\(\displaystyle{\small{\{f(x)g(x)\}’=\lim_{h\to0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}\cdots②}}\)
上式右辺の分子についてみてみます。
ここで、\(\{f(x)g(x+h)-f(x)g(x+h)\}\)を計算すると\(0\)となるのでこれを\(\bf{②式}\)に足しても問題ありません。
足すと、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&f(x+h)g(x+h)-f(x)g(x)+\{f(x)g(x+h)-f(x)g(x+h)\}\\\\=&&{f(x+h)-f(x)}g(x+h)+{g(x+h)-g(x)}f(x)\end{eqnarray}}}\)
となります。
定義式全体では、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\lim_{h\to0}\frac{{f(x+h)-f(x)}g(x+h)+{g(x+h)-g(x)}f(x)}{h}\\\\=&&\lim_{h\to0}\left\{\frac{f(x+h)-f(x)}{h}g(x+h)+\frac{g(x+h)-g(x)}{h}f(x)\right\}\end{eqnarray}}}\)
ここで、
\(\displaystyle{\lim_{h\to0}\frac{f(x+h)-f(x)}{h}}=f'(x)\)
\(\displaystyle{\lim_{h\to0}\frac{g(x+h)-g(x)}{h}}=g'(x)\)
また、
\(\displaystyle{\lim_{h\to0}g(x+h)=g(x)}\)
なので、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\lim_{h\to0}\left\{\frac{f(x+h)-f(x)}{h}g(x+h)+\frac{g(x+h)-g(x)}{h}f(x)\right\}\\\\=&&f'(x)g(x)+g'(x)f(x)\end{eqnarray}}}\)
すなわち、
\(\displaystyle{\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)}\)
となります。
\(\underline{\bf{積の微分計算例)}}\)
\(y=(x^2+1)(2x^2+4)\)を\(x\)で微分してみます。
展開して微分してもいいですが、今回は積の微分公式を使います。
\(f(x)=x^2+1\)
\(g(x)=2x^2+4\)
とすると、
\(f'(x)=2x\)
\(g'(x)=4x\)
となります。
ここで、積の微分公式を用いると、
\(\displaystyle{\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)}\)
なので、
\(\displaystyle{\begin{eqnarray}y’&=&\{(x^2+1)(2x^2+4)\}’\\\\&=&(x^2+1)'(2x^2+4)+(x^2+1)(2x^2+4)’\\\\&=&2x(2x^2+4)+(x^2+1)・4x\\\\&=&(4x^3+8x)+(4x^3+4x)\\\\&=&8x^3+12x\end{eqnarray}}\)
となります。
この積の微分公式を用いると、自然数\(n\)における\((x^n)’=nx^{n-1}\)を数学的帰納法で証明できます。
(「微分係数と導関数」では、二項定理を用いて証明した)
\(\underline{{\bf{帰納法を用いた}}{x^n}{\bf{の証明}}}\)
\(n=1\)のとき、\(x\)の微分は、
\(\displaystyle{\lim_{h\to0}\frac{(x+h)-x}{h}=1}\)
よって、\((x^n)’=nx^{n-1}\)は成り立つ。
\(n=k\)のとき、\((x^n)’=x^{n-1}\)が成り立つと仮定する。すなわち、\((x^k)’=kx^{k-1}\)が成り立つと仮定すると、
\(n=k+1\)のとき、積の微分公式を用いて、
\(\displaystyle{\begin{eqnarray}(x^{k+1})’&=&(x・x^{k})’\\\\&=&(x)’・x^k+x・(x^k)’\\\\&=&x^k+x・(kx^{k-1})\\\\&=&x^k+kx^k\\\\&=&(k+1)x^k\end{eqnarray}}\)
よって、\(n=k+1\)のときも成り立つ。
以上から、自然数\(n\)について
\((x^n)’=nx^{n-1}\)
が成り立つ。
☆自然数\(n\)について、
\((x^n)’=nx^{n-1}\)
2-2.商の微分公式
商の導関数に関する公式は、以下のようになります。
i) \(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{{g(x)}^2}}\)
ii) \(\displaystyle{\left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-f(x)g'(x)}{{g(x)}^2}}\)
上記商の導関数について証明します。
iについては、導関数の定義式から、iiについては積の微分公式とiの式から導きます。
\(\underline{\bf{iについて}}\)
導関数の定義式から、
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=\lim_{h\to0}\frac{\frac{1}{g(x+h)}-\frac{1}{g(x)}}{h}}\)
ここで、分子について通分すると
\(\displaystyle{\begin{eqnarray}&&\frac{1}{g(x+h)}-\frac{1}{g(x)}\\\\=&&\frac{g(x)}{g(x+h)g(x)}-\frac{g(x+h)}{g(x+h)g(x)}\\\\=&&\frac{g(x)-g(x+h)}{g(x+h)g(x)}\\\\=&&-\frac{g(x+h)-g(x)}{g(x+h)g(x)}\end{eqnarray}}\)
よって、定義式は、
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}\frac{\frac{1}{g(x+h)}-\frac{1}{g(x)}}{h}\\\\=&&\lim_{h\to0}{-\frac{g(x+h)-g(x)}{hg(x)g(x+h)}}\\\\=&&\lim_{h\to0}{-\frac{g(x+h)-g(x)}{h}・\frac{1}{g(x)g(x+h)}}\end{eqnarray}}\)
上式について、
\(\displaystyle{\lim_{h\to0}\frac{g(x+h)-g(x)}{h}}\)
は導関数の定義そのものなので、\(g'(x)\)となります。
また、\(h\to0\)とすると、\(g(x+h)\to{g(x)}\)となるので、
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}{-\frac{g(x+h)-g(x)}{h}・\frac{1}{g(x)g(x+h)}}\\\\=&&-\frac{g'(x)}{{g(x)}^2}\end{eqnarray}}\)
以上から、
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{{g(x)}^2}}\)
となります。
\(\underline{\bf{iiについて}}\)
\(\displaystyle{\left\{\frac{f(x)}{g(x)}\right\}’={f(x)・\frac{1}{g(x)}}’}\)
上式に対して、積の微分公式
\(\displaystyle{\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)}\)
を用いると、
\(\displaystyle{\begin{eqnarray}\left\{f(x)・\frac{1}{g(x)}\right\}’&=&f'(x)・\frac{1}{g(x)}+f(x)\left\{\frac{1}{g(x)}\right\}’\end{eqnarray}}\)
ここで、商の微分公式
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{{g(x)}^2}}\)
を用いると、
\(\displaystyle{\begin{eqnarray}&&f'(x)・\frac{1}{g(x)}+f(x)\left\{\frac{1}{g(x)}\right\}’\\\\=&&f'(x)・\frac{1}{g(x)}+f(x)・\left\{-\frac{g'(x)}{{g(x)}^2}\right\}\\\\=&&\frac{f'(x)g(x)}{{g(x)}^2}-\frac{f(x)g'(x)}{{g(x)}^2}\\\\=&&\frac{f'(x)g(x)-f(x)g'(x)}{{g(x)}^2}\end{eqnarray}}\)
以上から、
\(\displaystyle{\left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-f(x)g'(x)}{{g(x)}^2}}\)
となります。
上記の2つの公式に関してですが、
\(\displaystyle{\left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-f(x)g'(x)}{{g(x)}^2}}\)
さえ覚えておけば\(f(x)=1\)として、
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{{g(x)}^2}}\)
を
\(\displaystyle{\begin{eqnarray}\left\{\frac{1}{g(x)}\right\}’&=&\frac{(1)’g(x)-1・g'(x)}{{g(x)}^2}\\\\&=&\frac{0・g(x)-1・g'(x)}{{g(x)}^2}\\\\&=&-\frac{g'(x)}{{g(x)}^2}\end{eqnarray}}\)
のように、導くことができます。
下記に計算例を載せておきます。
iの計算例)
\(\displaystyle{y=\frac{1}{3x+1}}\)
を\(x\)で微分することを考えます。
\((3x+1)’=3\)
なので、商の微分公式
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{{g(x)}^2}}\)
から、
\(\displaystyle{\begin{eqnarray}y’&=&\left(\frac{1}{3x+1}\right)’\\\\&=&-\frac{(3x+1)’}{(3x+1)^2}\\\\&=&-\frac{3}{(3x+1)^2}\end{eqnarray}}\)
となります。
iiの計算例)
\(\displaystyle{y=\frac{x^2}{x+1}}\)
を\(x\)で微分することを考えます。
\((x^2)’=2x\)
\((x+1)’=1\)
なので、商の微分公式
\(\displaystyle{\left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-f(x)g'(x)}{{g(x)}^2}}\)
を用いて、
\(\displaystyle{\begin{eqnarray}y’&=&\left(\frac{x^2}{x+1}\right)’\\\\&=&\frac{(x^2)'(x+1)-x^2(x+1)’}{(x+1)^2}\\\\&=&\frac{2x(x+1)-x^2・1}{(x+1)^2}\\\\&=&\frac{(2x^2+2x)-x^2}{(x+1)^2}\\\\&=&\frac{x^2+2x}{(x+1)^2}\end{eqnarray}}\)
となります。
2-3.\(x^n\)の導関数(\(n\)が整数の時)
公式\((x^n)’=nx^{n-1}\)が正の整数(自然数)\(n\)について成り立つことは、これまでに示してきました。
商の微分公式を用いると、負の整数の場合にも成り立つことを示すことができます。
正の整数を\(m\)として、\(n=-m\)とすると、
\(\displaystyle{\begin{eqnarray}(x^n)’&=&(x^{-m})’\\\\&=&\left(\frac{1}{x^m}\right)’\end{eqnarray}}\)
これに、商の微分公式
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{{g(x)}^2}}\)
を用いて、
\(\displaystyle{\begin{eqnarray}\left(\frac{1}{x^m}\right)’&=&-\frac{(x^m)’}{{(x^m)}^2}\\\\&=&-\frac{mx^{m-1}}{x^{2m}}\end{eqnarray}}\)
\(\displaystyle{\frac{1}{x^{2m}}}\)を指数表示にすると、\(x^{-2m}\)となるので、
\(\displaystyle{\begin{eqnarray}-\frac{mx^{m-1}}{x^{2m}}&=&-m(x^{m-1})・(x^{-2m})\\\\&=&-mx^{m-1-(2m)}\\\\&=&-mx^{-m-1}\\\\&=&nx^{n-1} (∵n=-m)\end{eqnarray}}\)
従って、公式\((x^n)’=nx^{n-1}\)は\(n\)が負の整数についても成り立ちます。
また、\(n=0\)のとき、\(x^0=1\)なので、このときも上記公式は成り立ちます。
以上のことから、一般に
\(\textcolor{red}{{n}{\bf{が整数のとき}}}\)
\(\displaystyle{\textcolor{red}{(x^n)’=nx^{n-1}}}\)
となります。
3.合成関数の微分法
合成関数\(y=f(g(x))\)の導関数を、2つの関数\(y=f(u)\)と\(u=g(x)\)の導関数で表すことを考えてみます。
\(u\)の関数\(y=f(u)\)と、\(x\)の関数\(u=g(x)\)がともに微分可能なとき、\(x\)の増分\(\Delta{x}\)に対する\(u\)の増分を\(\Delta{u}\)、\(u\)の増分に対する\(y\)の増分を\(\Delta{y}\)とすると、\(\displaystyle{\frac{\Delta{y}}{\Delta{x}}}\)は、
\(\displaystyle{\frac{\Delta{y}}{\Delta{x}}=\frac{\Delta{y}}{\Delta{u}}・\frac{\Delta{u}}{\Delta{x}}}\)
と書けます。
このとき、\(\Delta{x}\to0\)のとき\(\Delta{u}\to0\)となります。
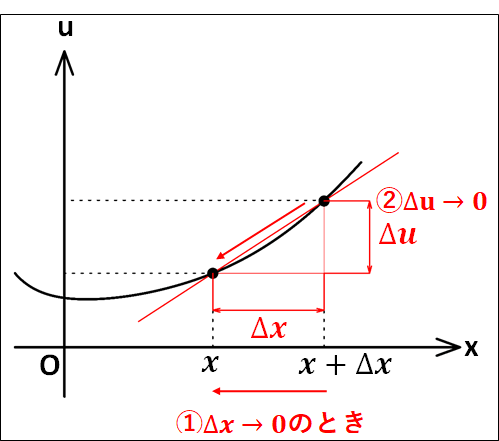
以上から、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\lim_{\Delta{x}\to0}\frac{\Delta{y}}{\Delta{x}}\\\\&=&\lim_{\Delta{x}\to0}\left(\frac{\Delta{y}}{\Delta{u}}・\frac{\Delta{u}}{\Delta{x}}\right)\\\\&=&\lim_{\Delta{u}\to0}\left(\frac{\Delta{y}}{\Delta{u}}\right)・\lim_{\Delta{x}\to0}\left(\frac{\Delta{u}}{\Delta{x}}\right)\\\\&=&\frac{dy}{du}・\frac{du}{dx}\end{eqnarray}}\)
となります。
よって、下記のことが成り立ちます。
\(y=f(u)\)が\(u\)の関数として微分可能で、\(u=g(x)\)が\(x\)の関数として微分可能であるとする。
このとき、合成関数\(y=f(g(x))\)は\(x\)の関数として微分可能で、
\(\displaystyle{\frac{dy}{dx}=\frac{dy}{du}・\frac{du}{dx}}\)
※感覚としては、約分して成り立つように表記する。
\(\displaystyle{\frac{dy}{dx}}\)を求めたいとき、
\(\displaystyle{\frac{dy}{\textcolor{blue}{\cancel{\textcolor{black}{du}}}}・\frac{\textcolor{blue}{\cancel{\textcolor{black}{du}}}}{dx}=\frac{dy}{dx}}\)
となるようにする。
\(\underline{\bf{合成関数の微分法計算例}}\)
\(y=(x^2+1)^3\)に関して、\(\displaystyle{\frac{dy}{dx}}\)を求めてみます。
\(u==x^2+1\)とすると、\(y=u^3\)
合成関数の微分法から、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\left(\frac{dy}{du}\right)・\left(\frac{du}{dx}\right)\\\\&=&\left\{\frac{d}{du}u^3\right\}・\left\{\frac{d}{dx}(x^2+1)\right\}\\\\&=&3u^2・2x\end{eqnarray}}\)
(※上記、\(\frac{d}{du}u^3\)は\(u^3\)を\(u\)で微分する、\(\frac{d}{dx}(x^2+1)\)は\((x^2+1)\)を\(x\)で微分するという意味になります。)
いま、\(u=x^2+1\)なので、\(u^2\)に代入すると、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&3u^2・2x\\\\&=&3(x^2+1)^2・2x\\\\&=&6x(x^2+1)^2\end{eqnarray}}\)
となります。
4.逆関数の微分法
4-1.逆関数の微分法
逆関数を利用して、もとの関数の導関数を求めてみます。
\(f(x)、g(x)\)が互いに逆関数でともに微分可能であるとします。
\(y=f(x)\)を\(x\)について解くと、\(x=g(y)\)
この両辺を\(x\)で微分すると、
\(\displaystyle{\begin{eqnarray}&&\frac{d}{dx}x=\frac{d}{dx}g(y)\\\\\Leftrightarrow&&1=\frac{d}{dx}g(y)\end{eqnarray}}\)
また、合成関数の微分法から、
\(\displaystyle{\begin{eqnarray}&&1=\frac{d}{dx}g(y)\\\\\Leftrightarrow&&1=\frac{d}{dy}g(y)・\frac{dy}{dx}\end{eqnarray}}\)
\(g(y)=x\)なので、
\(\displaystyle{\begin{eqnarray}&&1=\frac{d}{dy}g(y)・\frac{dy}{dx}\\\\\Leftrightarrow&&1=\frac{dx}{dy}・\frac{dy}{dx}\end{eqnarray}}\)
\(\displaystyle{\frac{dx}{dy}\neq0}\)のとき、上式の両辺を\(\displaystyle{\frac{dx}{dy}}\)で割って、
\(\displaystyle{\begin{eqnarray}&&1=\frac{dx}{dy}・\frac{dy}{dx}\\\\\Leftrightarrow&&\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}\end{eqnarray}}\)
となります。
従って、逆関数の微分法は下記のようになります。
\(\displaystyle{\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}}\)
\(\underline{\bf{逆関数の微分法計算例}}\)
\(\displaystyle{y=\sqrt{x}}\)の導関数を、逆関数の微分法を用いて求めてみます。
\(\displaystyle{y=\sqrt{x}}\)を\(x\)について解くと、\(\displaystyle{x=y^2}\)
以上から、逆関数の微分法を用いて、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\frac{1}{\frac{dx}{dy}}\\\\&=&\frac{1}{\frac{d}{dy}y^2}\\\\&=&\frac{1}{2y}\\\\&=&\frac{1}{2\sqrt{x}} (∵y=\sqrt{x})\end{eqnarray}}\)
となります。
4-2.\(x^p\)の導関数(\(p\)は有理数)
逆関数の微分法を用いて、\(p\)が有理数の場合の\(x^p\)の導関数を求めてみます。
\(p\)が有理数のとき、正の整数\(n\)と整数\(m\)を用いて、\(\displaystyle{p=\frac{m}{n}}\)と表せるので、
\(\displaystyle{x^p=x^{\frac{n}{m}}=\left(x^{\frac{1}{n}}\right)^m}\)
ここで、\(\displaystyle{y=x^{\frac{1}{n}}}\)とおくと、\(x\)について解いて\(x=y^n\)となります。
これより、
\(\displaystyle{\frac{dx}{dy}=ny^{n-1}}\)
また、
\(\displaystyle{x^p=\left(x^{\frac{1}{n}}\right)^m=y^m}\)
となります。
以上のことを用いて、
\(\displaystyle{\begin{eqnarray}\frac{d}{dx}x^p&=&\frac{d}{dx}y^m\\\\&=&\frac{d}{dy}y^m・\frac{dy}{dx}(←合成関数の微分法)\\\\&=&(my^{m-1})・\frac{1}{\frac{dx}{dy}}(←逆関数の微分法)\\\\&=&(my^{m-1})・\frac{1}{ny^{n-1}}(∵\frac{dx}{dy}=ny^{n-1})\\\\&=&(my^{m-1})・\frac{1}{n}・y^{-(n-1)}\\\\&=&\frac{m}{n}y^{m-1-(n-1)}\\\\&=&\frac{m}{n}y^{m-n}\\\\&=&\frac{m}{n}\left(x^{\frac{1}{n}}\right)^{m-n}(∵y=x^{\frac{1}{n}})\\\\&=&\frac{m}{n}x^{\frac{m}{n}-1}\\\\&=&px^{p-1}(∵p=\frac{m}{n})\end{eqnarray}}\)
よって、\(p\)が有理数のとき
\(\displaystyle{\left(x^p\right)’=px^{p-1}}\)
となります。
下記に計算例を載せておきます。
\(\underline{\bf{計算例}}\)
逆関数の微分法でも扱った、\(y=\sqrt{x}\)を\(x\)で微分します。
\(\displaystyle{y=\sqrt{x}=x^{\frac{1}{2}}}\)
なので、\(\displaystyle{\left(x^p\right)’=px^{p-1}}\)を用いて
\(\displaystyle{\begin{eqnarray}\left(\sqrt{x}\right)’&=&\left(x^{\frac{1}{2}}\right)’\\\\&=&\frac{1}{2}x^{\frac{1}{2}-1}\\\\&=&\frac{1}{2}x^{-\frac{1}{2}}\\\\&=&\frac{1}{2}・\frac{1}{x^{\frac{1}{2}}}\\\\&=&\frac{1}{2\sqrt{x}}\end{eqnarray}}\)
となります。
この計算結果は、逆関数の微分法を用いて計算したものと同じとなっています。
5.様々な関数の導関数
5-1.三角関数の導関数
各三角関数の導関数を調べてみます。
\(\underline{{\sin{x}}{\bf{の導関数}}}\)
導関数の定義式から、
\(\displaystyle{\lim_{h\to0}\frac{\sin{(x+h)}-\sin{x}}{h}}\)
また、「三角関数の公式」で扱った加法定理を用いると、\(\sin{(x+h)}\)は
\(\sin{(x+h)}=\sin{x}\cos{h}+\cos{x}\sin{h}\)
となるので、定義式は
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}\frac{\sin{(x+h)}-\sin{x}}{h}\\\\=&&\lim_{h\to0}\frac{\sin{x}\cos{h}+\cos{x}\sin{h}-\sin{x}}{h}\\\\=&&\lim_{h\to0}\frac{(\cos{h}-1)\sin{x}+\cos{x}\sin{h}}{h}\\\\=&&\lim_{h\to0}\left\{\frac{(\cos{h}-1)\sin{x}}{h}+\frac{\cos{x}\sin{h}}{h}\right\} \cdots①\end{eqnarray}}\)
ここで、
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}\frac{(\cos{h}-1)}{h}\\\\=&&\lim_{h\to0}\frac{(\cos{h}-1)(\cos{h}+1)}{h(\cos{h}+1)}\\\\=&&\lim_{h\to0}\frac{\cos^2{h}-1}{h(\cos{h}+1)}\\\\=&&\lim_{h\to0}\frac{-\sin^2{h}}{h(\cos{h}+1)} (∵\sin^2{\theta}+\cos^2{\theta}=1)\\\\=&&\lim_{h\to0}\left(\frac{-\sin{h}}{h}・\frac{\sin{h}}{\cos{h}+1}\right)\end{eqnarray}}\)
上式において、「極限」で扱った\(\displaystyle{\lim_{x\to0}\frac{\sin{x}}{x}=1}\)を用います。
また、\(h\to0\)のとき、\(\sin{h}\to0\) , \(\cos{h}\to1\)なので、
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}\left(\frac{-\sin{h}}{h}・\frac{\sin{h}}{\cos{h}+1}\right)\\\\=&&(-1)・\frac{0}{1+1}\\\\=&&0\end{eqnarray}}\)
よって、\(①\)は、
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}\left\{\frac{(\cos{h}-1)}{h}・\sin{x}+\frac{\sin{h}}{h}・\cos{x}\right\}\\\\=&&0・\sin{x}+1・\cos{x}\\\\=&&\cos{x}\end{eqnarray}}\)
以上から、
\(\textcolor{red}{(\sin{x})’=\cos{x}}\)
となります。
\(\underline{{\cos{x}}{\bf{の導関数}}}\)
\(\displaystyle{\cos{x}=\sin(x+\frac{\pi}{2})}\)なので、\(\displaystyle{u=x+\frac{\pi}{2}}\)とおくと
\(\displaystyle{\cos{x}=\sin(x+\frac{\pi}{2})=\sin{u}}\)
また、
\(\displaystyle{\frac{du}{dx}=\left(x+\frac{\pi}{2}\right)’=1}\)
これらより、
\(\displaystyle{\begin{eqnarray}(\cos{x})’&=&\frac{d}{dx}\sin(x+\frac{\pi}{2})\\\\&=&\frac{d}{dx}\sin{u}\\\\&=&\frac{d}{du}\sin{u}\frac{du}{dx}(←合成関数の微分)\\\\&=&\cos{u}・1\\\\&=&\cos(x+\frac{\pi}{2})\\\\&=&-\sin{x}\end{eqnarray}}\)
以上から、
\(\textcolor{red}{(\cos{x})’=-\sin{x}}\)
\(\underline{{\tan{x}}{\bf{の導関数}}}\)
\(\displaystyle{\tan{x}=\frac{\sin{x}}{\cos{x}}}\)より、積の微分公式から、
\(\displaystyle{\begin{eqnarray}(\tan{x})’&=&\left(\sin{x}・\frac{1}{\cos{x}}\right)’\\\\&=&(\sin{x})’・\frac{1}{\cos{x}}+\sin{x}・\left(\frac{1}{\cos{x}}\right)’\\\\&=&\frac{\cos{x}}{\cos{x}}+\sin{x}・\left(\frac{1}{\cos{x}}\right)’\\\\&=&1+\sin{x}・\left(\frac{1}{\cos{x}}\right)’ \cdots②\end{eqnarray}}\)
ここで、\(\displaystyle{y=\frac{1}{\cos{x}} , u=\cos{x}}\)とすると、
\(\displaystyle{y=\frac{1}{\cos{x}}=\frac{1}{u}=u^{-1}}\)
また、
\(\displaystyle{\frac{du}{dx}=(\cos{x})’=-\sin{x}}\)
よって、合成関数の微分公式から
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\frac{dy}{du}・\frac{du}{dx}\\\\&=&\frac{d}{du}u^{-1}\frac{d}{dx}(\cos{x})\\\\&=&-u^{-2}・(-\sin{x})\\\\&=&\frac{\sin{x}}{u^2}\\\\&=&\frac{\sin{x}}{\cos^2{x}} (∵u=\cos^{x})\end{eqnarray}}\)
このことから、
\(\displaystyle{\left(\frac{1}{\cos{x}}\right)’=\frac{\sin{x}}{\cos^2{x}}}\)
これらから、\(②\)は
\(\displaystyle{\small{\begin{eqnarray}1+\sin{x}・\left(\frac{1}{\cos{x}}\right)’&=&1+\sin{x}・\frac{\sin{x}}{\cos^2{x}}\\\\&=&1+\frac{\sin^2{x}}{\cos^2{x}}\\\\&=&\frac{\cos^2{x}}{\cos^2{x}}+\frac{\sin^2{x}}{\cos^2{x}}\\\\&=&\frac{\sin^2{x}+\cos^2{x}}{\cos^2{x}}\\\\&=&\frac{1}{\cos^2{x}}(∵\sin^2{x}+\cos^2{x}=1)\end{eqnarray}}}\)
以上から、
\(\displaystyle{(\tan{x})’=\frac{1}{\cos^2{x}}}\)
となります。
5-2.対数関数の導関数
対数関数については、こちらも参考にしてください
→対数関数
\(\underline{{\bf{ネイピア数}}{e}{\bf{の定義}}}\)
数学において、\(e\)をネイピア数といい、その値は\(e=2.718\cdots\)と続く無理数となります。
この\(e\)の定義は、下記のようになります。
\(\displaystyle{e=\lim_{h\to0}\left(1+h\right)^{\frac{1}{h}}}\)
また、上式において\(h\to0\)で\(\frac{1}{h}\to\infty\)であればよいので、下式でも表せます。
\(\displaystyle{e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n}\)
これらがネイピア数\(e\)の定義となります。
この\(e\)を底とする対数(\(\log_e{x}\)など)を自然対数といい、微分法や積分法では底の\(e\)を省略して単に\(\log{x}\)と書くことが多いです。
\(\underline{{\bf{対数関数}}{\log_a{x} (a\gt0,a\neq1)}{\bf{の導関数}}}\)
導関数の定義式から、
\(\displaystyle{\scriptsize{\begin{eqnarray}(&&\log_a{x})’\\\\=&&\lim_{h\to0}\frac{\log_a{(x+h)}-\log_a{x}}{h}\\\\=&&\lim_{h\to0}\frac{1}{h}\left\{\log_a\left(\frac{x+h}{x}\right)\right\}(←対数の性質から)\\\\=&&\lim_{h\to0}\frac{1}{h}\left\{\log_a\left(1+\frac{h}{x}\right)\right\}\\\\=&&\lim_{h\to0}\frac{1}{x}・\frac{x}{h}\left\{\log_a\left(1+\frac{h}{x}\right)\right\}(←(1+k)^{\frac{1}{k}}の形を作りたい)\\\\=&&\lim_{h\to0}\frac{1}{x}\log_a\left(1+\frac{h}{x}\right)^{\frac{x}{h}}(←対数の性質から)\end{eqnarray}}}\)
ここで、\(\displaystyle{\frac{h}{x}=k}\)とおくと、\(h\to0\)のとき\(k\to0\)なので上式は、
\(\displaystyle{\begin{eqnarray}&&\lim_{h\to0}\frac{1}{x}\log_a\left(1+\frac{h}{x}\right)^{\frac{x}{h}}\\\\=&&\frac{1}{x}\lim_{k\to0}\log_a(1+k)^{\frac{1}{k}}\end{eqnarray}}\)
\(\displaystyle{}\lim_{k\to0}(1+k)^{\frac{1}{k}}\)は\(e\)の定義となるので
\(\displaystyle{\begin{eqnarray}&&\frac{1}{x}\lim_{k\to0}\log_a(1+k)^{\frac{1}{k}}\\\\=&&\frac{1}{x}\log_a{e}\end{eqnarray}}\)
となります。
さらに\(\log_a{e}\)について底の変換公式を用いて底を\(e\)に変換すると
\(\displaystyle{\begin{eqnarray}\log_a{e}&=&\frac{\log_e{e}}{\log_e{a}}\\\\&=&\frac{1}{\log{a}}(←\log_e{e}=1,底eは省略)\end{eqnarray}}\)
よって、
\(\displaystyle{\frac{1}{x}\log_a{e}=\frac{1}{x\log{a}}}\)
以上から、
\(\displaystyle{\textcolor{red}{(\log_a{x})’=\frac{1}{x\log{a}}}}\)
特に、\(a=e\)のとき、\(\log_e{e}=1\)なので、\(\log{x}\)を微分すると
\(\displaystyle{(\log{x})’=\frac{1}{x\log{e}}=\frac{1}{x}}\)
となります。
\(\underline{{\bf{関数}}{\log|x|}{\bf{の導関数}}}\)
\(x\)の正負で場合分けをして考えていきます。
i) \(x\gt0\)のとき
\(\log|x|=\log{x}\)なので、
\(\displaystyle{\begin{eqnarray}(\log|x|)’&=&(\log{x})’\\\\&=&\frac{1}{x}\end{eqnarray}}\)
ii) \(x\lt0\)のとき
\(\log|x|=\log(-x)\)
よって、\(y=\log(-x) , u=-x\)とおくと、\(y=\log{u}\)
合成関数の微分公式から、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\frac{dy}{du}・\frac{du}{dx}\\\\&=&\frac{d}{du}\log{u}・\frac{d}{dx}(-x)\\\\&=&\frac{1}{u}・(-1)\\\\&=&\frac{1}{-x}・(-1)(∵u=-x)\\\\&=&\frac{1}{x}\end{eqnarray}}\)
よって、\(x\lt0\)のときも
\(\displaystyle{(\log|x|)’=\frac{1}{x}}\)
以上から、
\(\displaystyle{\textcolor{red}{(\log|x|)’=\frac{1}{x}}}\)
となります。
また、\(\log_a{|x|}\)については、底を\(e\)に変換すると
\(\displaystyle{\log_a{|x|}=\frac{\log{|x|}}{\log{a}}}\)
なので、
\(\displaystyle{\begin{eqnarray}(\log_a|x|)’&=&\frac{1}{\log{a}}(\log|x|)'(←\frac{1}{\log{a}}は定数)\\\\&=&\frac{1}{\log{a}}・\frac{1}{x}\\\\&=&\frac{1}{x\log{a}}\end{eqnarray}}\)
従って、
\(\displaystyle{\textcolor{red}{(\log_a{|x|})’=\frac{1}{x\log{a}}}}\)
となります。
5-3.指数関数の導関数
指数関数については、こちらも参考にしてください
→指数関数
\(y=a^x (a\gt0,a\neq1)\)の導関数を求めてみます。
上記関数を\(x\)について解くと
\(x=\log_a{y}\)
また、対数関数の導関数の公式から、
\(\displaystyle{\frac{dx}{dy}=\frac{d}{dy}\log_a{y}=\frac{1}{y\log{a}}}\)
よって、逆関数の微分公式から、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\frac{1}{\frac{dx}{dy}}\\\\&=&\frac{1}{\frac{1}{y\log{a}}}\\\\&=&y\log{a}\\\\&=&a^x\log{a} (∵y=a^x)\end{eqnarray}}\)
以上から、
\(\displaystyle{\textcolor{red}{(a^x)’=a^x\log{a}}}\)
また、特に\(a=e\)のとき、すなわち\(y=e^x\)のとき\(\log{e}=1\)となるので、
\(\displaystyle{(e^x)’=e^x\log{e}=e^x}\)
となります。
5-4.第n次導関数
関数\(y=f(x)\)の導関数\(f'(x)\)は\(x\)の関数となりますが、この\(f'(x)\)が微分可能であるとき、さらに微分して得られる導関数を、関数\(y=f(x)\)の第2次導関数といい、\(\displaystyle{y^{\prime\prime},f^{\prime\prime}(x),\frac{d^2y}{dx^2},\frac{d^2}{dx^2}f(x)}\)などで表します。
さらに、\(f”(x)\)の導関数を\(y=f(x)\)の第3次導関数といい、\(\displaystyle{y^{\prime\prime\prime},f^{\prime\prime\prime}(x),\frac{d^3y}{dx^3},\frac{d^3}{dx^3}f(x)}\)などで表します。
一般に関数\(y=f(x)\)を\(n\)回微分して得られる関数を\(y=f(x)\)の第\(n\)次導関数といい、\(\displaystyle{y^{(n)},f^{(n)}(x),\frac{d^ny}{dx^n},\frac{d^n}{dx^n}f(x)}\)などで表します。
\((y^{(1)},y^{(2)},y^{(3)}\)はそれぞれ\(y^{\prime},y^{\prime\prime},y^{\prime\prime\prime})\)
例)
\(y=x^3\)とするとき
\(\displaystyle{\frac{dy}{dx}=3x^2}\) ←第1次導関数
\(\displaystyle{\frac{d^2y}{dx^2}=\frac{d}{dx}3x^2=6x}\) ←第2次導関数
\(\displaystyle{\frac{d^3y}{dx^3}=\frac{d}{dx}6x=6}\) ←第3次導関数
5-5.\(x^a\)の導関数(\(a\)は実数)
\(a\)が実数のときの\(x^a\)の導関数について考えてみます。
\(y=x^a\)の両辺の自然対数をとると、
\(\log{y}=\log{x^a}=a\log{x}\)
上式の両辺を\(x\)で微分すると、
\(\displaystyle{\frac{d}{dx}\log{y}=\frac{d}{dx}(a\log{x})}\)
ここで、左辺について合成関数の微分法を用いると
\(\displaystyle{\begin{eqnarray}\frac{d}{dx}\log{y}&=&\frac{d}{dy}\log{y}・\frac{dy}{dx}\end{eqnarray}}\)
対数関数の微分公式から
\(\displaystyle{\frac{d}{dy}\log{y}=\frac{1}{y}}\)
また、
\(\displaystyle{\frac{dy}{dx}=y’}\)
なので、
\(\displaystyle{\frac{d}{dy}\log{y}・\frac{dy}{dx}=\frac{y’}{y}}\)
右辺については、対数関数の微分公式から
\(\displaystyle{\frac{d}{dx}(a\log{x})=\frac{a}{x}}\)
よって、
\(\displaystyle{\begin{eqnarray}&&\frac{d}{dx}\log{y}=\frac{d}{dx}(a\log{x})\\\\\Leftrightarrow&&\frac{y’}{y}=\frac{a}{x}\\\\\Leftrightarrow&&{y’}=\frac{a}{x}y\end{eqnarray}}\)
\(y=x^a\)なので、上式を計算していくと、
\(\displaystyle{\begin{eqnarray}y’&=&\frac{a}{x}y\\\\&=&\frac{a}{x}x^a\\\\&=&a・x^a・x^{-1}\\\\&=&ax^{a-1}\end{eqnarray}}\)
以上から、\(a\)が実数のときについても
\(\displaystyle{\textcolor{red}{(x^a)’=ax^{a-1}}}\)
となります。
6.曲線の媒介変数表示と導関数
曲線\(C\)上の点\(P(x,y)\)の\(x\)座標と\(y\)座標が1つの変数\(t\)の関数\(f(t) , g(t)\)によって
\(x=f(t)\)
\(y=g(t)\)
と表されるとき、この表し方を曲線\(C\)の媒介変数表示といい、\(t\)を媒介変数またはパラメータといいます。
このときの\(\displaystyle{\frac{dy}{dx}}\)を考えると、合成関数と逆関数の微分法から、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\frac{dy}{dt}・\frac{dt}{dx}\\\\&=&\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\\\\&=&\frac{g'(t)}{f'(t)}\end{eqnarray}}\)
となります。
例) \(x=t^2,y=3t\)のとき
\(\displaystyle{\frac{dx}{dt}=2t}\)
\(\displaystyle{\frac{dy}{dt}=3}\)
よって、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dx}&=&\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\\\\&=&\frac{3}{2t}\end{eqnarray}}\)
となります。
今回は以上となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


