投稿日:
【高校物理】対数関数【高校数学】【対数】
\(\require{color}\)
\(\require{cancel}\)
対数関数の基礎的な内容となるので、予習復習したい方向けです。
対数関数のことを分かっているよという方は、読み飛ばして頂いてかまいません。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.対数について
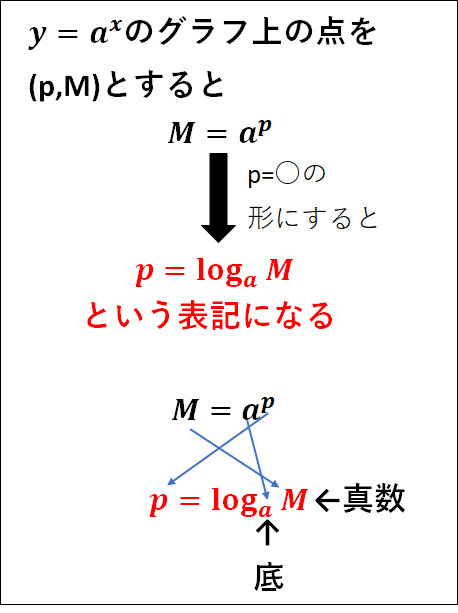
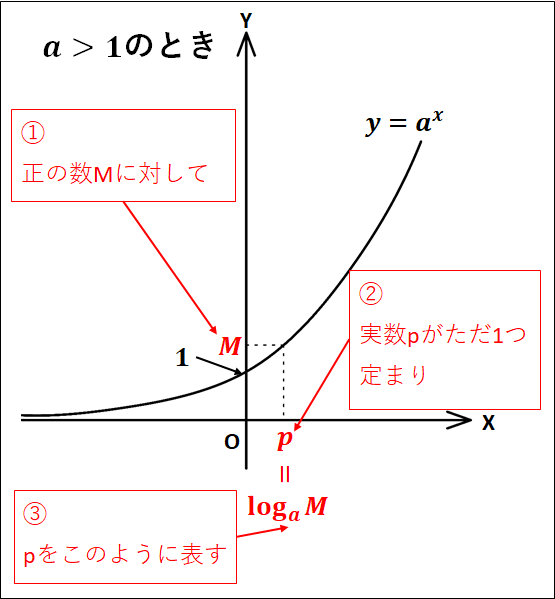
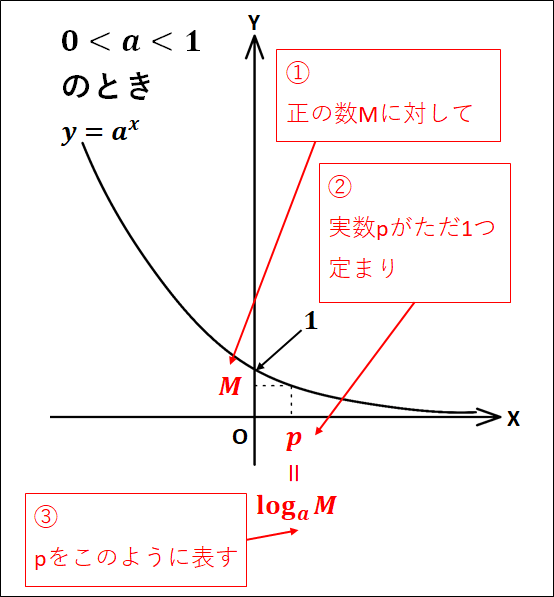
指数関数\(y=a^x\)を考えると、どんな正の数\(M\)に対しても\(M=a^p\)となる実数\(p\)がただ一つに定まります。
この\(p\)を\(\log_a{M}\)で表し、これを\(a\)を底とする\(M\)の対数といいます。
また、\(\log_a{M}\)における正の数\(M\)をこの対数の真数といいます。
(※\(10\)を底とする対数を常用対数という)
(指数関数についてはこちらも参考にしてください→指数関数)
以上から、指数と対数の関係は次のようになります。
\(a\gt0\) , \(a\neq1\)で、\(M\gt0\)のとき、
\(M=a^p \Leftrightarrow p=\log_a{M}\)
以下に例を載せておきます。
例1)
\(8=2^3\)を[指数=○]の形(対数表示)で表すと、
\(3=\log_2{8}\)
となる。
例2)
\(\log_3{27}=x\)を考えてみる。
上記式を[真数=○]の形(指数表示)で表すと、
\(27=3^x\)
ここで、\(27=3^3\)であるから上式は
\(3^3=3^x\)
となる。
指数を比較すると\(x=3\)となるので、最初の式から
\(\log_3{27}=3\)
となる。
また、\(M=a^p\)のとき、\(\log_a{M}=p\)なので
\(\log_a{a^p}=p\)
となります。
(\(\log_a{M}=p\)の\(M\)に\(M=a^p\)を代入した)
2.対数の性質
対数の性質として、以下のようなものがあります。
\(1=a^0\)なので、\(M=a^p\Leftrightarrow\log_a{M}=p\)から
\(\log_a{1}=0\)
\(a=a^1\)なので、\(M=a^p\Leftrightarrow\log_a{M}=p\)から
\(\log_a{a}=1\)
上記2式が成り立ちます。
また、指数法則から成り立つ性質もあり、以下のようになります。
\(M\gt0\) , \(N\gt0\) , \(k\)を実数とすると、
\(\log_a{MN}=\log_a{M}+\log_a{N} \cdots①\)
\(\displaystyle{\log_a{\frac{M}{N}}=\log_a{M}-\log_a{N} \cdots②}\)
\(\log_a{M^k}=k\log_a{M} \cdots③\)
それぞれの計算例を載せておきます。
(計算例は左辺→右辺への式変形の例となります)
例)
\(\underline{\bf{①の例}}\)
\(\begin{eqnarray}\log_{15}{3}+\log_{15}{5}&=&\log_{15}{(3×5)}\\\\&=&\log_{15}{15}\\\\&=&1\end{eqnarray}\)
\(\underline{\bf{②の例}}\)
\(\displaystyle{\begin{eqnarray}\log_2{12}-\log_2{3}&=&\log_2{\left(\frac{12}{3}\right)}\\\\&=&\log_2{4}\\\\&=&\log_2{(2^2)}\\\\&=&2\end{eqnarray}}\)
(\(\log_2{(2^2)}\)は指数表示に直すと、\(2^2=2^p\)となり、指数を比較すると\(p=2\)となる)
\(\underline{\bf{③の例}}\)
\(\begin{eqnarray}3\log_2{4}&=&\log_2{(4^3)}\\\\&=&\log_2{{(2^2)}^3}\\\\&=&\log_2{(2^6)}\\\\&=&6\end{eqnarray}\)
次に、なぜ上記の性質が成り立つのかを説明していきます。
\(\underline{\bf{①について}}\)
\(\log_a{M}=p , \log_a{N}=q\)とすると、
\(M=a^p , N=a^q\)
となります。
よって、
\(MN=a^p×a^q=a^{p+q}\)
これを対数表示すると
\(\begin{eqnarray}\log_a{MN}&=&{p+q}\\\\&=&\log_a{M}+\log_a{N}\end{eqnarray}\)
となります。
\(\underline{\bf{②について}}\)
\(①\)と同様に、\(\log_a{M}=p , \log_a{N}=q\)とすると、
\(M=a^p , N=a^q\)
よって、
\(\displaystyle{\frac{M}{N}=\frac{a^p}{a^q}=a^{p-q}}\)
これを対数表示すると
\(\displaystyle{\begin{eqnarray}\log_a{\frac{M}{N}}&=&p-q\\\\&=&\log_a{M}-\log_a{N}\end{eqnarray}}\)
となります。
\(\underline{\bf{③について}}\)
\(\log_a{M}=p\)とすると、\(M=a^p\)となります。
よって、
\(M^k={(a^p)}^k=a^{kp}\)
従って、
\(\begin{eqnarray}\log_a{M^k}&=&kp\\\\&=&k\log_a{M}\end{eqnarray}\)
となります。
3.底の変換公式
底の変換公式とは、\(a\)を底とする対数\(\log_a{b}\)を\(c\)を底とする対数に変換する公式です。
底の変換公式は以下のようになります。
\(a , b , c\)は正の数で\(a\neq1 , c\neq1\)とするとき、
\(\displaystyle{\log_a{b}}=\frac{\log_c{b}}{\log_c{a}}\)
底の変換公式を用いた計算例を載せておきます。
例)底が\(4\)の対数を底が\(2\)のものに変換するとき
\(\displaystyle{\begin{eqnarray}\log_4{16}&=&\frac{\log_2{16}}{\log_2{4}}\\\\&=&\frac{\log_2{2^4}}{\log_2{2^2}}\\\\&=&\frac{4}{2}\\\\&=&2\end{eqnarray}}\)
となります。
底の変換公式は、以下のように導きます。
\(a , b , c\)は正の数で\(a\neq1 , c\neq1\)とします。
\(\log_a{b}=p\)とすると\(b=a^p\)なので、両辺\(c\)を底とする対数をとると、
\(\log_c{b}=\log_c{a^p}=p\log_c{a}\)
よって、
\(\log_c{b}=p\log_c{a}\)
\(a\neq1\)から、\(\log_c{a}\neq0\)なので、上式の両辺を\(\log_c{a}\)で割って、
\(\displaystyle{p=\frac{\log_c{b}}{\log_c{a}}}\)
ここで、\(p=\log_a{b}\)なので、
\(\displaystyle{\log_a{b}=\frac{\log_c{b}}{\log_c{a}}}\)
となります。
4.対数関数
\(a\)を\(1\)とは異なる正の定数とするとき、\(y=\log_a{x}\)は\(x\)の関数となります。
この関数を\(\textcolor{red}{a}\)\(\textcolor{red}{\bf{を底とする}}\)\(\textcolor{red}{x}\)\(\textcolor{red}{\bf{の対数関数}}\)といいます。
一般に、対数関数\(y=\log_a{x}\)のグラフは、\(y=a^x\)のグラフと直線\(y=x\)に関して対称であり、次のようになります。
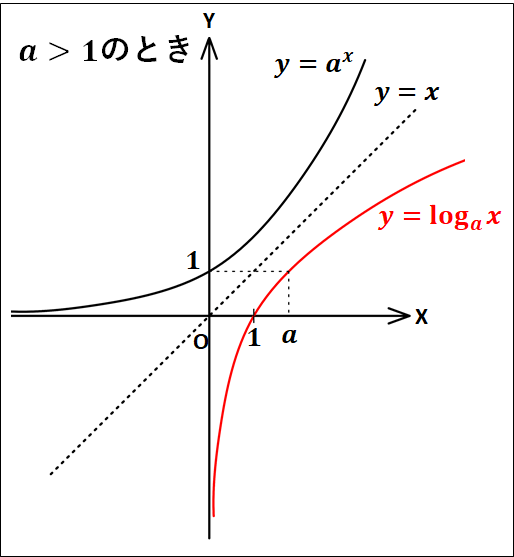
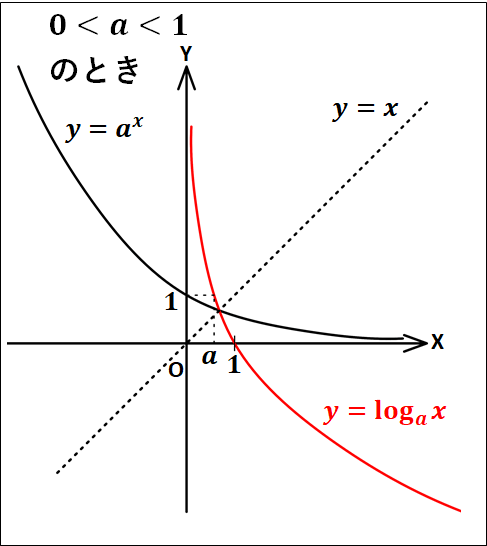
対数関数に関して、どちらの場合も(y)軸が漸近線(グラフが近づく線)となります。
また、\(y=0\)のとき、\(0=\log_a{x}\)となる\(x\)は、\(x=a^0=1\)から\(1\)となります。
\(y=1\)のとき、\(1=\log_a{x}\)となる\(x\)は、\(x=a^1=a\)から\(a\)となります。
従って、これらのグラフはどちらも点\((1 , 0) 、(a , 1)\)を通ります。
そして、曲線は\(a\gt1\)のとき右上がり、\(0\lt{a}\lt1\)のとき右下がりとなります。
対数関数\(y=\log_a{x}\)の特徴は以下のようになります。
○定義域は正の数全体で、値域は実数全体である。
○\(a\gt1\)のとき、増加関数である。すなわち、
\(0{\lt}p{\lt}r\Leftrightarrow\log_a{p}\lt\log_a{q}\)
○\(0\lt{a}\lt1\)のとき、減少関数である。すなわち
\(0{\lt}p{\lt}r\Leftrightarrow\log_a{p}\gt\log_a{q}\)
となります。
今回は以上になります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


