投稿日:
【高校物理】三角関数③/三角関数の公式【高校数学】【三角関数】
\(\require{color}\)
\(\require{cancel}\)
三角関数には、公式が存在します。
この中には、簡単に導けるものもありますが覚えておいた方がよいものもあります。
高校物理の範囲では、使用しないものもあるとは思いますが一通りの公式はこの記事で紹介していこうと思います。
三角関数に関する記事は、こちらも参考にしてください。
→三角関数の定義と関係式
→三角関数のグラフ
→練習問題1(定義とグラフ)
→練習問題2(三角方程式と公式)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.三角関数の性質に関するもの
1-1.周期に関する公式
周期に関する公式は、以下の3つになります。
\(\sin(\theta+2n\pi)=\sin\theta\)
\(\cos(\theta+2n\pi)=\cos\theta\)
\(\tan(\theta+n\pi))=\tan\theta\)
これらの公式は、三角関数の周期に関するもので、\(\sin\theta\) ,\(\cos\theta\)は周期が\(2\pi\)なので、\(2\pi\)の整数倍毎に同じ形が繰り返されることに基づいています。
\(\tan\theta\)は周期が\(\pi\)なので、\(\pi\)の整数倍毎に同じ形が繰り返されます。
(周期の話についてはこちらも参考に→三角関数の定義と関係式)
1-2.\((-\theta)\)に関する公式
\((-\theta)\)に関する公式は、以下の3つになります。
\(\sin(-\theta)=-\sin\theta\)
\(\cos(-\theta)=\cos\theta\)
\(\tan(-\theta)=-\tan\theta\)
これらは単位円で考えると分かりやすいと思います。
単位円の原点を\(O\)とし、単位円上の点を\(P\),\(P^{\prime}\)とします。
\(P\),\(P^{\prime}\)の位置は、\(x\)軸と\(OP\)がなす角が\(\theta\)、\(x\)軸と\(OP^{\prime}\)がなす角が\(-\theta\)とします。
また、点\(P\)および点\(P^{\prime}\)から\(x\)軸に垂直に下した線分と\(x\)軸との交点を点\(A\)とします。
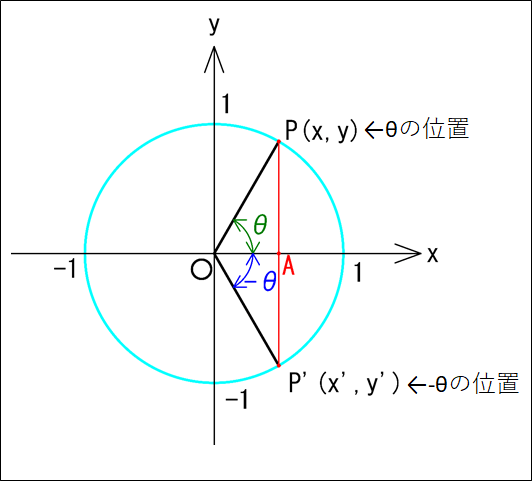
図から、点\(P\)の\(x\)座標は\(\cos\theta\)、\(y\)座標は\(\sin\theta\)なので、
\(x=\cos\theta\)
\(y=\sin\theta\)
また、辺の長さで考えると
\(OA\)は三角形\(OPA\)と\(OP’A\)で共通
\(AP=AP’\)
となります。
点\(P’\)について、\((x’,y’)\)を\(\theta\)を用いて表してみると、\(x’\)座標は辺\(OA\)が共通なので
\(x’=x=\cos\theta\)
\(y’\)座標は、辺の長さが\(AP=AP’\)であり符合は\(y\)の値を負にしたものなので、
\(y’=-y=-\sin\theta\)
となります。
以上から、
\(P(\cos\theta ,\sin\theta)\)
\(→(\thetaを-\thetaにすると)\)
\(→P'(\cos(-\theta) ,\sin{(-\theta)})=P'(\cos\theta ,-\sin{\theta})\)
よって、
\(\cos(-\theta)=\cos\theta\)
\(\sin(-\theta)=-\sin\theta\)
となります。
また、\(\tan(-\theta)\)は、
\(\displaystyle{\begin{eqnarray}\tan(-\theta)&=&\frac{\sin(-\theta)}{\cos(-\theta)}\\\\&=&\frac{-\sin\theta}{\cos\theta}\\\\&=&-\frac{\sin\theta}{\cos\theta}\\\\&=&-\tan\theta\end{eqnarray}}\)
となります。
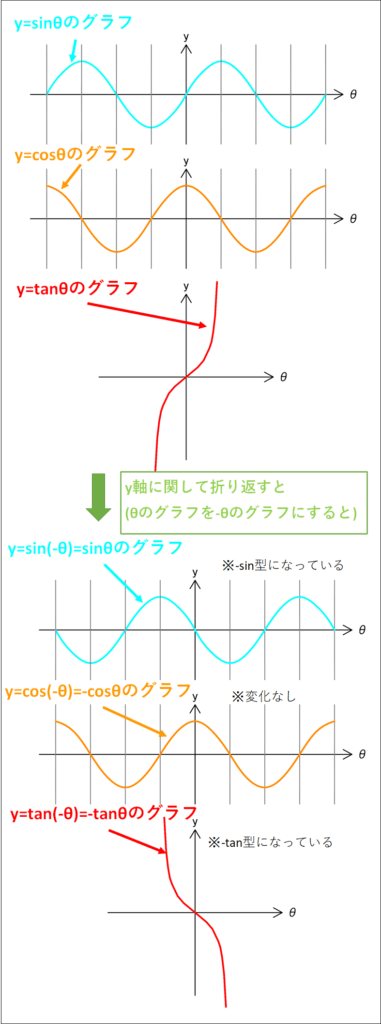
今回は単位円で考えましたが、グラフで考えることもできます。
その際には、それぞれのグラフを\(y\)軸に関して折り返したものを考えます。
\(y=\sin\theta\)のグラフは、\(y=-\sin\theta\)のグラフに、
\(y=\cos\theta\)のグラフは、\(y\)軸に関して対称なので、\(y=\cos\theta\)のグラフに、
\(y=\tan\theta\)のグラフは、\(y=-\tan\theta\)のグラフに、
それぞれなることが分かると思います。
1-3.\((\theta+\pi)\)に関する公式
\((\theta+\pi)\)に関する公式は、以下の3つになります。
\(\sin(\theta+\pi)=-\sin\theta\)
\(\cos(\theta+\pi)=-\cos\theta\)
\(y=\tan(\theta+\pi)=\tan\theta\)
これらの公式も\((-\theta)\)に関するものと同様に単位円を用いて考えていきます。
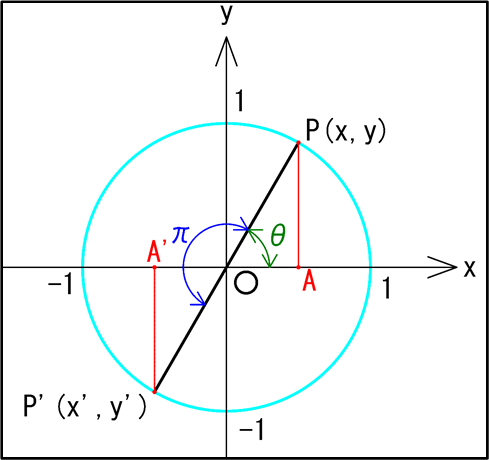
同様にして、単位円上に点\(P(x,y)\)と点\(P'(x’,y’)\)をとります。
点\(P\)と点\(P’\)の条件は、単位円の中心を原点\(O\)とすると、
点\(P\)→\(x\)軸と線分\(OP\)のなす角が\(\theta\)
点\(P’\)→\(x\)軸と線分\(OP’\)とのなす角が\((\theta+\pi)\)
また、点\(P\)と点\(P’\)から\(x\)軸に垂直に引いた線分と、\(x\)軸との交点をそれぞれ点\(A\)、点\(A’\)とします。
\(\pi=180^{\circ}\)なので、図示すると下のようになります。
点\(P\)の座標は、これまでと同様に、
\(x=\cos\theta\)
\(y=\sin\theta\)
となります。
また辺の長さを考えると、\(\angle{A’OP’}=\theta\)となります。(対頂角なので)
このことから、三角形\(OAP\)と\(OA’P’\)は合同となるので辺の長さは、
\(OA=OA’\)
\(AP=A’P’\)
となります。
次に、\(P’\)の座標を考えていきます。
\(x’\)は\(OA=OA’\)と図から\(x\)を負にしたものなので、
\(x’=-x=-\cos\theta\)
となります。
\(y’\)は\(AP=A’P’\)と図から\(y\)を負にしたものなので、
\(y’=-y=-\sin\theta\)
となります。
以上から、
\(P(\cos\theta,\sin\theta)\)
\(→(\thetaを(\theta+\pi)にすると)\)
\(→P'(\cos(\theta+\pi) ,\sin(\theta+\pi))=P'(-\cos\theta ,-\sin\theta)\)
となります。
また、\(\tan(\theta+\pi)\)は”1-1.周期に関するもの”でも説明したように、\(\tan\theta\)の周期は\(\pi\)なので\(\pi\)毎に同じ形が繰り返されます。
よって、
\(\tan(\theta+\pi)=\tan\theta\)
となります。
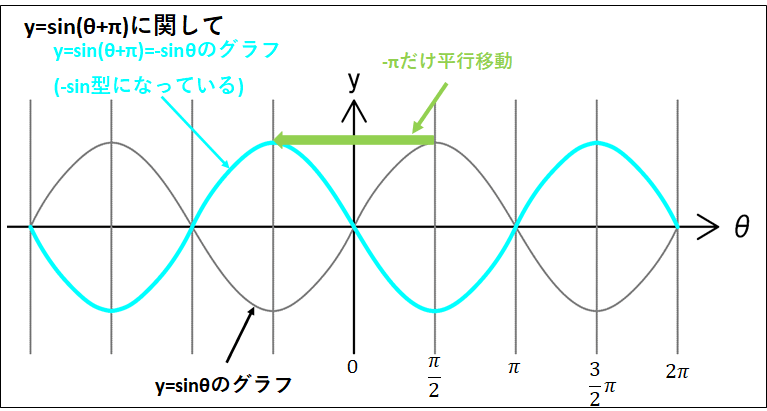
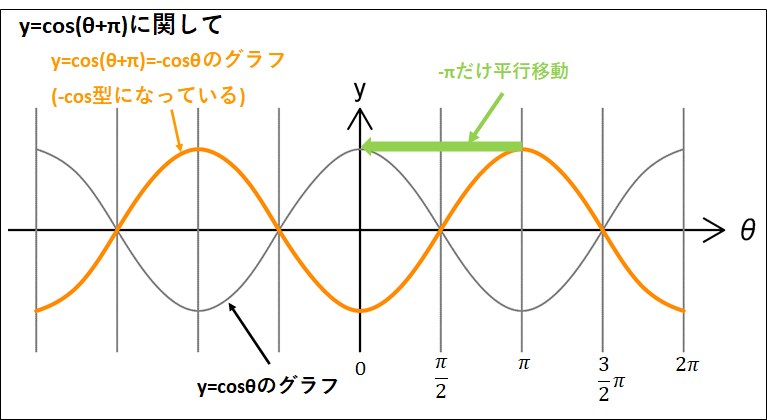
ここでも、\(\sin(\theta+\pi)\)と\(\cos(\theta+\pi)\)についてグラフで考えてみます。
これら三角関数のグラフはそれぞれ、\(\sin\theta\)と\(\cos\theta\)のグラフを\(\theta\)軸方向へ\(-\pi\)だけ平行移動したものになります。
(グラフの平行移動に関しては、こちらも参考にしてください→三角関数のグラフ)
このことをグラフで確認してみると、それぞれ、
\(\sin(\theta+\pi)=-\sin\theta\)
\(\cos(\theta+\pi)=-\cos\theta\)
になっていることが確認できると思います。
1-4.\((\theta+\frac{\pi}{2})\)に関する公式
\(\displaystyle{(\theta+\frac{\pi}{2})}\)に関する公式は、以下の3つになります。
\(\displaystyle{\sin(\theta+\frac{\pi}{2})=\cos\theta}\)
\(\displaystyle{ \cos(\theta+\frac{\pi}{2})=-\sin\theta}\)
\(\displaystyle{ \tan(\theta+\frac{\pi}{2})=-\frac{1}{\tan\theta}}\)
これらの公式も、単位円を用いて考えていきます。
単位円上に点\(P(x,y)\)と点\(P'(x’,y’)\)をとります。
点\(P\)と点\(P’\)の条件は、単位円の中心を原点\(O\)とすると、
点\(P\)→\(x\)軸と線分\(OP\)のなす角が\(\theta\)
点\(P’\)→\(x\)軸と線分\(OP’\)とのなす角が\((\theta+\frac{\pi}{2})\)
また、点\(P\)から\(x\)軸に垂直に引いた線分と\(x\)軸との交点を点\(A\)、点\(P’\)から\(y\)軸に垂直に引いた線分と\(y\)軸との交点を点\(B\)とします。
図示すると以下のようになるのですが、なぜ\(\angle{BOP’}=\theta\)となるのかを説明していきます。
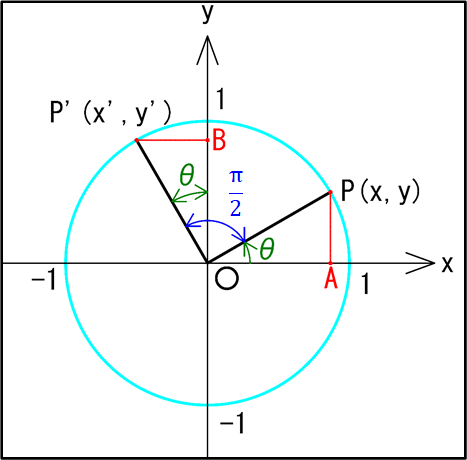
それぞれの角度について考えてみると、
\(\displaystyle{\textcolor{red}{\angle{AOP}=\theta }\cdots①}\)
\( \displaystyle{\textcolor{blue}{\angle{AOB}=\frac{\pi}{2}} \cdots②}\)
\( \displaystyle{\textcolor{#ffd700}{\angle{POP’}=\frac{\pi}{2}} \cdots③}\)
加えて、\(\textcolor{blue}{\angle{AOB}}\)は\(\textcolor{red}{\angle{AOP}}\)と\(\textcolor{green}{\angle{POB}}\)を足したものなので
\(\textcolor{blue}{\angle{AOB}}=\textcolor{red}{\angle{AOP}}+ \textcolor{green}{\angle{POB}} \cdots④\)
\(\textcolor{#ffd700}{\angle{POP’}}\)は \(\textcolor{green}{\angle{POB}}\) と\(\angle{BOP’}\)を足したものなので
\(\textcolor{#ffd700}{\angle{POP’}}=\textcolor{green}{\angle{POB}}+\angle{BOP’} \cdots⑤\)
以上から、\(\angle{BOP’}\)を求めていきます。
まず、\(①,②,④\)から、
\(\displaystyle{\begin{eqnarray}\textcolor{blue}{\angle{AOB}}&=&\textcolor{red}{\angle{AOP}}+\textcolor{green}{\angle{POB}}\\\\\Leftrightarrow\textcolor{green}{\angle{POB}}&=&\textcolor{blue}{\angle{AOB}}-\textcolor{red}{\angle{AOP}}\\\\&=&\frac{\pi}{2}-\theta\end{eqnarray}}\)
よって、
\(\displaystyle{\textcolor{green}{\angle{POB}}=\frac{\pi}{2}-\theta \cdots⑥}\)
また、\(③,⑤,⑥\)から、
\(\displaystyle{\begin{eqnarray}\textcolor{#ffd700}{\angle{POP’}}&=&\textcolor{green}{\angle{POB}}+\angle{BOP’}\\\\\Leftrightarrow\angle{BOP’}&=&\textcolor{#ffd700}{\angle{POP’}}-\textcolor{green}{\angle{POB}}\\\\&=&\frac{\pi}{2}-(\frac{\pi}{2}-\theta)\\\\&=&\theta\end{eqnarray}}\)
以上から、
\(\displaystyle{\angle{BOP’}=\theta}\)
となります。
この単位円から、それぞれ\(\sin(\theta+\frac{\pi}{2})\)と\(\cos(\theta+\frac{\pi}{2})\)がどのようになるのかをみていきます。
図から、三角形\(OPA\)と\(OP’B\)は合同なので辺の長さは、
\(OA=OB\)
\(PA=P’B\)
となります。
このことから、
\((点Pのx座標の絶対値)=(点P’のy座標の絶対値)\)
\((点Pのy座標の絶対値)=(点P’のx座標の絶対値)\)
となります。
また、図から符号も考えると
\(x’=-y=-\sin\theta\)
\(y’=x=\cos\theta\)
となります。
以上から、
\(P(\cos\theta,\sin\theta)\)
\(→(\thetaを(\theta+\frac{\pi}{2})にすると)\)
\(→P'(\cos(\theta+\frac{\pi}{2}) ,\sin(\theta+\frac{\pi}{2}))=P'(-\sin\theta ,\cos\theta)\)
よって、
\(\displaystyle{\cos(\theta+\frac{\pi}{2})=-\sin\theta}\)
\(\displaystyle{\sin(\theta+\frac{\pi}{2})=\cos\theta}\)
となります。
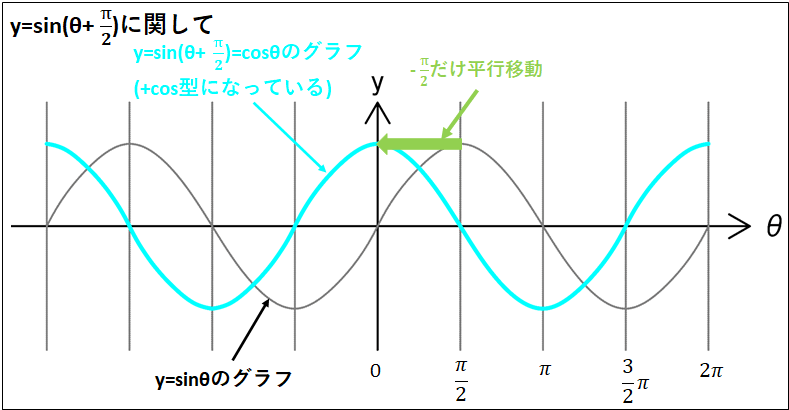
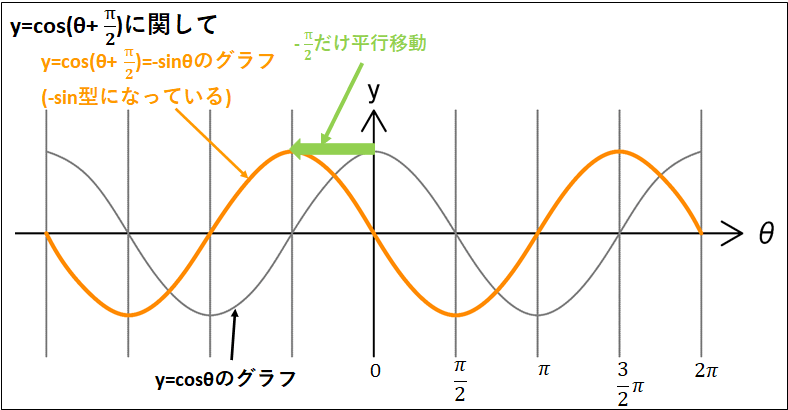
\(\sin(\theta+\frac{\pi}{2})\)と\(\cos(\theta+\frac{\pi}{2})\)をグラフで考えると、\((\theta+\pi)\)の時と同様に\(\sin\theta\)と\(\cos\theta\)のグラフをそれぞれ\(\theta\)軸方向へ\(-\frac{\pi}{2}\)平行移動したものなので、以下のようになります。
それぞれ、
\(\sin(\theta+\frac{\pi}{2})=\cos\theta\)
\(\cos(\theta+\frac{\pi}{2})=-\sin\theta\)
となっていることを確認してみてください。
\(\tan(\theta+\frac{\pi}{2})\)については定義から、
\(\displaystyle{\begin{eqnarray}\tan(\theta+\frac{\pi}{2})&=&\frac{\sin(\theta+\frac{\pi}{2})}{\cos(\theta+\frac{\pi}{2})}\\\\&=&\frac{\cos\theta}{-\sin\theta}\\\\&=&-\frac{1}{\frac{\sin\theta}{\cos\theta}}\\\\&=&-\frac{1}{\tan\theta}\end{eqnarray}}\)
となります。
2.加法定理
加法定理に関する\((\alpha+\beta)\)の公式は以下の6つになります。
\(\displaystyle{\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \cdots①}\)
\(\displaystyle{\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \cdots②}\)
\(\displaystyle{\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \cdots③}\)
\(\displaystyle{\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \cdots④}\)
\(\displaystyle{\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \cdots⑤}\)
\(\displaystyle{\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \cdots⑥}\)
証明は省略しますが、以上が加法定理の公式となります。
私自身も暗記は好きではないのですが、最低\(①\)と\(③\)の式は覚えておく必要があります。
\(①\)と\(③\)の式はきれいな形なので、覚えれないことはないと思います。
また、\(②\)の式は\(①\)の式の間のプラスをマイナスにして、\(④\)の式は\(③\)の式の間のマイナスをプラスにするとでてきます。
または、\(\cos(-\beta)=\cos\beta\) ,\(\sin(-\beta)=-\sin\theta\)を用いて
\(①\)から、\(\beta\)を\(-\beta\)にして
\(\displaystyle{\begin{eqnarray}\sin(\alpha-\beta)&=&\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta)\\&=&\sin\alpha\cos\beta-\cos\alpha\sin\beta\end{eqnarray}}\)
また、\(③\)から\(\beta\)を\(-\beta\)にして
\(\displaystyle{\begin{eqnarray}\cos(\alpha-\beta)&=&\cos\alpha\cos(-\beta)-\sin\alpha\sin(-\beta)\\&=&\cos\alpha\cos\beta+\sin\alpha\sin\beta\end{eqnarray}}\)
としても導けます。
\(\tan\)の加法定理は、いつものように定義から、
\(\displaystyle{\begin{eqnarray}\tan(\alpha+\beta)&=&\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\\\\&=&\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\\\\&=&\frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}+\frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta}-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} \\\\&&(↑分子分母を\cos\alpha\cos\betaで割った)\\\\&=&\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\tan(\alpha-\beta)&=&\frac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)}\\\\&=&\frac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\cos\alpha\cos\beta+\sin\alpha\sin\beta}\\\\&=&\frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}-\frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta}+\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\\\&&(↑分子分母を\cos\alpha\cos\betaで割った)\\\\&=&\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\end{eqnarray}}\)
として導出できますし、\(\tan(\alpha+\beta)\)か\(\tan(\alpha-\beta)\)のどちらかを導出できれば、その間の符号を逆にしたものがもう一方の公式となります。
このように最低でも\(①\)と\(②\)の式を覚えていれば、他の加法定理の公式は導出できますので、覚えておきましょう。
最後に、高校数学の範囲を超えているので受験での証明問題などでは使用できませんが、オイラーの公式を用いた\(\sin\)と\(\cos\)の加法定理の導き方を紹介しておきます。
余談になるので、興味がなければ読み飛ばしてください。
→目次へ戻る
以下が、オイラーの公式になります。
\(\displaystyle{e^{i\theta}=\cos\theta+i\sin\theta}\)
上記の式は認めるとします。
式の中にある\(“i”\)は虚数単位という2乗して-1になる数です。なので\(i^2=-1\)が成り立ちます。
また、詳しい説明は省略しますが、\(“i”\)が掛かっていない部分を”実部”、\(“i”\)が掛かっている部分を”虚部”といいます。
オイラーの公式の中でいうと、\(i\)が掛かっていない\(\textcolor{red}{\underline{\cos\theta}}\)が実部、\(i\)が掛かっている\(\textcolor{red}{\underline{\sin\theta}}\)が虚部になります。
ここまでの内容で、加法定理を導いていきます。
オイラーの公式の\(\theta\)を\(\alpha+\beta\)に置き換えて
\(\displaystyle{e^{i(\alpha+\beta)}=\textcolor{blue}{\cos(\alpha+\beta)}+i\textcolor{green}{\sin(\alpha+\beta) }\cdots①}\)
また、指数法則から
\(\displaystyle{e^{i(\alpha+\beta)}=e^{i\alpha}e^{i\beta}}\)
となります。
\(e^{i\alpha}\)と\(e^{i\beta}\)はオイラーの公式の\(\theta\)をそれぞれ\(\alpha\)と\(\beta\)に置き換えて
\(e^{i\alpha}=\cos\alpha+i\sin\alpha\)
\(e^{i\beta}=\cos\beta+i\sin\beta\)
よって、
\(\displaystyle{\begin{eqnarray}e^{i(\alpha+\beta)}&=&e^{i\alpha}e^{i\beta}\\&=&(\cos\alpha+i\sin\alpha)(\cos\beta+i\sin\beta)\\\\&=&\cos\alpha\cos\beta+i\sin\beta\cos\alpha\\&&+i\sin\alpha\cos\beta+i^{2}\sin\alpha\sin\beta\\\\&&(i^{2}=-1なので)\\\\&=&\textcolor{blue}{(\cos\alpha\cos\beta-\sin\alpha\sin\beta)}\\&&+i\textcolor{green}{(\sin\alpha\cos\beta+\cos\alpha\sin\beta)} \cdots②\end{eqnarray}}\)
ここで、\(①\)と\(②\)の”実部”と”虚部”をそれぞれ比較します。
\(①\)の”実部”は\(\textcolor{blue}{\cos(\alpha+\beta)}\)、\(②\)の”実部”は\(\textcolor{blue}{(\cos\alpha\cos\beta-\sin\alpha\sin\beta)}\)なので比較すると
\(\displaystyle{\textcolor{blue}{\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta}}\)
\(①\)の”虚部”は\(\textcolor{green}{\sin(\alpha+\beta)}\)、\(②\)の”虚部”は\(\textcolor{green}{(\sin\alpha\cos\beta+\cos\alpha\sin\beta)}\)なので比較すると
\(\displaystyle{\textcolor{green}{\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta}}\)
以上から、加法定理の公式である
\(\displaystyle{\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta}\)
\(\displaystyle{\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta}\)
が導けました。
ここでは導きませんが、同様にして\(\sin(\alpha-\beta)\)、\(cos(\alpha-\beta)\)も導けるので、興味があれば導出してみてください。
3.倍角に関する公式
3-1.2倍角の公式
2倍角の公式は、以下の5つになります。
\(\sin2\alpha=2\sin\alpha\cos\alpha \cdots①\)
\(\cos2\alpha=\cos^2\alpha-\sin^2\alpha \cdots②\)
\(\cos2\alpha=1-2\sin^2\alpha \cdots③\)
\(\cos2\alpha=2\cos^2\alpha-1 \cdots④\)
\(\displaystyle{\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha} \cdots⑤}\)
これらの公式は、加法定理を変形したり三角関数の関係式を用いて導出することができます。
\(\mathbf{\underline{①について}}\)
加法定理の式\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)の\(\beta\)を\(\alpha\)にして導きます。
\(\displaystyle{\begin{eqnarray}\sin2\alpha&=&\sin(\alpha+\alpha)\\&=&\sin\alpha\cos\alpha+\cos\alpha\sin\alpha\\&=&2\sin\alpha\cos\alpha\end{eqnarray}}\)
となります。
\(\mathbf{\underline{②について}}\)
\(①\)と同様に、加法定理の式\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)の\(\beta\)を\(\alpha\)にして導きます。
\(\displaystyle{\begin{eqnarray}\cos2\alpha&=&\cos(\alpha+\alpha)\\&=&cos\alpha\cos\alpha-\sin\alpha\sin\alpha\\&=&\cos^2\alpha-\sin^2\alpha\end{eqnarray}}\)
となります。
\(\mathbf{\underline{③について}}\)
\(②\)の式と三角関数の関係式\(\sin^2\theta+\cos^2\theta=1\)から導きます。
方針としては、\(②\)の式の右辺を\(\sin\)だけの形にしたいので、\(\cos\)を消去します。
三角関数の関係式の\(\theta\)を\(\alpha\)に置き換え、式変形をして、
\(\displaystyle{\begin{eqnarray}&&\sin^2\alpha+\cos^2\alpha=1\\\Leftrightarrow&&\cos^2\alpha=1-\sin^2\alpha\end{eqnarray}}\)
これを、\(②\)の式に代入して、
\(\displaystyle{\begin{eqnarray}\cos2\alpha&=&\cos^2\alpha-\sin^2\alpha\\&=&(1-\sin^2\alpha)-\sin^2\alpha\\&=&1-2\sin^2\alpha\end{eqnarray}}\)
となります。
\(\mathbf{\underline{④について}}\)
こちらも同様にして、\(②\)の式と三角関数の関係式\(\sin^2\theta+\cos^2\theta=1\)から導きます。
方針としては、\(②\)の式の右辺を\(\cos\)だけの形にしたいので、\(\sin\)を消去します。
三角関数の関係式の\(\theta\)を\(\alpha\)に置き換え、式変形をして、
\(\displaystyle{\begin{eqnarray}&&\sin^2\alpha+\cos^2\alpha=1\\\Leftrightarrow&&\sin^2\alpha=1-\cos^2\alpha\end{eqnarray}}\)
これを、\(②\)の式に代入して、
\(\displaystyle{\begin{eqnarray}\cos2\alpha&=&\cos^2\alpha-\sin^2\alpha\\&=&\cos^2\alpha-(1-\cos^2\alpha)\\&=&2\cos^2\alpha-1\end{eqnarray}}\)
となります。
\(\mathbf{\underline{⑤について}}\)
\(\tan2\alpha\)の式も同様にして、加法定理の式\(\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)の\(\beta\)を\(\alpha\)にして導きます。
\(\displaystyle{\begin{eqnarray}\tan2\alpha&=&\tan(\alpha+\alpha)\\\\&=&\frac{\tan\alpha+\tan\alpha}{1-\tan\alpha\tan\alpha}\\\\&=&\frac{2\tan\alpha}{1-\tan^2\alpha}\end{eqnarray}}\)
となります。
3-2.3倍角の公式
3倍角の公式は、以下の3つになります。
\(\sin3\alpha=3\sin\alpha-4\sin^3\alpha \cdots①\)
\(\cos3\alpha=4\cos^3\alpha-3\cos\alpha \cdots②\)
\(\displaystyle{\tan3\alpha=\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha} \cdots③}\)
これらの公式はすべて、加法定理の公式の\(+\beta\)を\(+2\alpha\)として、2倍角の公式と三角関数の関係式を用いると導くことができます。
\(\mathbf{\underline{①について}}\)
加法定理の式\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)の\(\beta\)を\(2\alpha\)として、
\(\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha\)
これを、2倍角の公式と三角関数の関係式\(\sin^2\alpha+\cos^2\alpha=1\)を用いて、\(\sin\alpha\)だけがでてくるように式変形をすると、
\(\displaystyle{\begin{eqnarray}\sin3\alpha&=&\sin(\alpha+2\alpha)\\\\&=&\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha\\\\&=&\sin\alpha(1-2\sin^2\alpha)+\cos\alpha・2\sin\alpha\cos\alpha\\\\&&(↑2倍角の公式を用いた)\\\\&=&\sin\alpha-2\sin^3\alpha+2\sin\alpha\cos^2\alpha\\\\&=&\sin\alpha-2\sin^3\alpha+2\sin\alpha(1-\sin^2\alpha)\\\\&&(↑三角関数の関係式を用いた)\\\\&=&\sin\alpha-2\sin^3\alpha+2\sin\alpha-2\sin^3\alpha\\\\&=&3\sin\alpha-4\sin^3\alpha\end{eqnarray}}\)
となります。
\(\mathbf{\underline{②について}}\)
\(②\)についても同様にして、加法定理の式\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)の\(\beta\)を\(2\alpha\)として、
\(\cos(\alpha+2\alpha)=\cos\alpha\cos2\alpha-\sin\alpha\sin2\alpha\)
これを、2倍角の公式と三角関数の関係式\(\sin^2\alpha+\cos^2\alpha=1\)を用いて、\(\cos\alpha\)だけがでてくるように式変形をすると、
\(\displaystyle{\begin{eqnarray}\cos3\alpha&=&\cos(\alpha+2\alpha)\\\\&=&\cos\alpha\cos2\alpha-\sin\alpha\sin2\alpha\\\\&=&\cos\alpha(2\cos^2\alpha-1)-\sin\alpha(2\sin\alpha\cos\alpha)\\\\&&(↑2倍角の公式を用いた)\\\\&=&2\cos^3\alpha-\cos\alpha-2\sin^2\alpha\cos\alpha\\\\&=&2\cos^3\alpha-\cos\alpha-2(1-\cos^2\alpha)\cos\alpha\\\\&&(↑三角関数の関係式を用いた)\\\\&=&2\cos^3\alpha-\cos\alpha-2\cos\alpha+2\cos^3\alpha\\\\&=&4\cos^3\alpha-3\cos\alpha\end{eqnarray}}\)
となります。
\(\mathbf{\underline{③について}}\)
これも同様にして、加法定理の式\(\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)の\(\beta\)を\(2\alpha\)として求めます。
\(\displaystyle{\begin{eqnarray}\tan3\alpha&=&\frac{\tan\alpha+\tan2\alpha}{1-\tan\alpha\tan2\alpha}\\\\&=&\frac{\tan\alpha+\frac{2\tan\alpha}{1-\tan^2\alpha}}{1-\frac{2\tan^2\alpha}{1-\tan^2\alpha}}\\\\&&(↑2倍角の公式を用いた)\\\\&=&\frac{\tan\alpha(1-\tan^2\alpha)+2\tan\alpha}{1-\tan^2\alpha-2\tan^2\alpha}\\\\&&(↑分子分母に(1-\tan^2\alpha)を掛けた)\\\\&=&\frac{\tan\alpha-\tan^3\alpha+2\tan\alpha}{1-3\tan^2\alpha}\\\\&=&\frac{3\tan\alpha-\tan^3\alpha}{1-3\tan^2\alpha}\end{eqnarray}}\)
となります。
3倍角の公式については以上となりますが、これらもオイラーの公式を用いて導くことができます。
オイラーの公式の\(\theta\)を\(3\alpha\)として、
\(e^{i(3\alpha)}=\cos3\alpha+i\sin3\alpha\)
また、指数法則から、
\((e^{i\alpha})^3=(\cos3\alpha+i\sin3\alpha)^3\)
これを計算していき、実部と虚部を比較すると導けるので、興味があればやってみてください。
3-3.半角の公式
半角の公式は、以下の3つになります。
\(\displaystyle{\sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2} \cdots①}\)
\(\displaystyle{\cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2} \cdots②}\)
\(\displaystyle{\tan^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha} \cdots③}\)
これらの公式は、2倍角の公式から導きます。
コサインの2倍角の公式\(\cos2\alpha=1-2\sin^2\alpha\)と\(\cos2\alpha=2\cos^2\alpha-1\)からそれぞれ、
\(\displaystyle{\begin{eqnarray}&&\cos2\alpha=1-2\cos^2\alpha\\\\\Leftrightarrow&&\sin^2\alpha=\frac{1-\cos2\alpha}{2} \cdots④\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}&&\cos2\alpha=2\cos^2\alpha-1\\\\\Leftrightarrow&&\cos^2\alpha=\frac{1+\cos2\alpha}{2} \cdots⑤\end{eqnarray}}\)
\(④\),\(⑤\)の\(\alpha\)をそれぞれ\(\frac{\alpha}{2}\)とすると、
\(\displaystyle{\begin{eqnarray}\sin^2\frac{\alpha}{2}&=&\frac{1-\cos(2\cdot\frac{\alpha}{2})}{2}\\\\&=&\frac{1-\cos\alpha}{2}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\cos^2\frac{\alpha}{2}&=&\frac{1+\cos(2\cdot\frac{\alpha}{2})}{2}\\\\&=&\frac{1+\cos\alpha}{2}\end{eqnarray}}\)
となります。
また、\(\tan\frac{\alpha}{2}\)についてはこれまでと同様に定義から、
\(\displaystyle{\begin{eqnarray}\tan^2\frac{\alpha}{2}&=&\frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}}\\\\&=&\frac{\frac{1-\cos\alpha}{2}}{\frac{1+\cos\alpha}{2}}\\\\&=&\frac{1-\cos\alpha}{1+\cos\alpha}\end{eqnarray}}\)
となります。
4.和と積の変換公式
4-1.積→和・差への変換公式
積から和や差への変換公式は以下の4つになります。
\(\displaystyle{\sin\alpha\cos\beta=\frac{1}{2}{\sin(\alpha+\beta)+\sin(\alpha-\beta)} \cdots①}\)
\(\displaystyle{\cos\alpha\sin\beta=\frac{1}{2}{\sin(\alpha+\beta)-\sin(\alpha-\beta)} \cdots②}\)
\(\displaystyle{\cos\alpha\cos\beta=\frac{1}{2}{\cos(\alpha+\beta)+\cos(\alpha-\beta)} \cdots③}\)
\(\displaystyle{\sin\alpha\sin\beta=-\frac{1}{2}{\cos(\alpha+\beta)-\cos(\alpha-\beta)} \cdots④}\)
これらの公式は、それぞれ加法定理の式を足したり引いたりして導きます。
これまでに解説したように(\sin)と(\cos)の加法定理の式は、以下の4つになります。
\(\displaystyle{\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \cdots⑤}\)
\(\displaystyle{\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \cdots⑥}\)
\(\displaystyle{\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \cdots⑦}\)
\(\displaystyle{\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \cdots⑧}\)
上記加法定理の式から、
\(①\)は\((⑤+⑥)\)から、
\(\displaystyle{\begin{eqnarray}&&\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta\\\\\Leftrightarrow&&\sin\alpha\cos\beta=\frac{1}{2}{\sin(\alpha+\beta)+\sin(\alpha-\beta)}\end{eqnarray}}\)
となります。
他の公式も同様にして、
\(②\)は\((⑤-⑥)\)から、
\(\displaystyle{\begin{eqnarray}&&\sin(\alpha+\beta)-\sin(\alpha-\beta)=2\cos\alpha\sin\beta\\\\\Leftrightarrow&&\cos\alpha\sin\beta=\frac{1}{2}{\sin(\alpha+\beta)-\sin(\alpha-\beta)}\end{eqnarray}}\)
\(③\)は\((⑦+⑧)\)から、
\(\displaystyle{\begin{eqnarray}&&\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta\\\\\Leftrightarrow&&\cos\alpha\cos\beta=\frac{1}{2}{\cos(\alpha+\beta)+\cos(\alpha-\beta)}\end{eqnarray}}\)
\(④\)は\((⑦-⑧)\)から、
\(\displaystyle{\begin{eqnarray}&&\cos(\alpha+\beta)-\cos(\alpha-\beta)=-2\sin\alpha\sin\beta\\\\\Leftrightarrow&&\sin\alpha\sin\beta=-\frac{1}{2}{\cos(\alpha+\beta)-\cos(\alpha-\beta)}\end{eqnarray}}\)
以上のように導くことができます。
4-2.和・差→積への変換公式
和や差から積への変換公式は以下の4つになります。
\(\displaystyle{{\sin}A+{\sin}B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2} \cdots⑨}\)
\(\displaystyle{{\sin}A-{\sin}B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2} \cdots⑩}\)
\(\displaystyle{{\cos}A+{\cos}B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2} \cdots⑪}\)
\(\displaystyle{{\cos}A-{\cos}B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2} \cdots⑫}\)
これらの公式は、積から和や差への変換公式から導くことができます。
\(\alpha+\beta=A \cdots⑬\)
\(\alpha-\beta=B \cdots⑭\)
とおくと、
\((⑬+⑭)\)から
\(\displaystyle{2\alpha=A+B\Leftrightarrow\alpha=\frac{A+B}{2}}\)
\((⑬-⑭)\)から
\(\displaystyle{2\beta=A-B\Leftrightarrow\beta=\frac{A-B}{2}}\)
これらを、積から和や差の変換公式\((①~④)\)に代入すると、
\(⑨\)は
\(\displaystyle{\begin{eqnarray}&&\sin\alpha\cos\beta=\frac{1}{2}{\sin(\alpha+\beta)+\sin(\alpha-\beta)}\\\\\Leftrightarrow&&\sin\frac{A+B}{2}\cos\frac{A-B}{2}=\frac{1}{2}{{\sin}A+{\sin}B}\\\\\Leftrightarrow&&{\sin}A+{\sin}B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}\end{eqnarray}}\)
となります。
他の公式も同様にして、
\(⑩\)は
\(\displaystyle{\begin{eqnarray}&&\cos\alpha\sin\beta=\frac{1}{2}{\sin(\alpha+\beta)-\sin(\alpha-\beta)}\\\\\Leftrightarrow&&\cos\frac{A+B}{2}\sin\frac{A-B}{2}=\frac{1}{2}{{\sin}A-{\sin}B}\\\\\Leftrightarrow&&{\sin}A-{\sin}B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2}\end{eqnarray}}\)
\(⑪\)は
\(\displaystyle{\begin{eqnarray}&&\cos\alpha\cos\beta=\frac{1}{2}{\sin(\alpha+\beta)+\cos(\alpha-\beta)}\\\\\Leftrightarrow&&\cos\frac{A+B}{2}\cos\frac{A-B}{2}=\frac{1}{2}{{\cos}A+{\cos}B}\\\\\Leftrightarrow&&{\cos}A+{\cos}B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}\end{eqnarray}}\)
\(⑫\)は
\(\displaystyle{\begin{eqnarray}&&\sin\alpha\sin\beta=-\frac{1}{2}{\cos(\alpha+\beta)-\cos(\alpha-\beta)}\\\\\Leftrightarrow&&\sin\frac{A+B}{2}\sin\frac{A-B}{2}=-\frac{1}{2}{{\cos}A-{\cos}B}\\\\\Leftrightarrow&&{\cos}A-{\cos}B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2}\end{eqnarray}}\)
となります。
和と積の変換公式については以上となります。
5.三角関数の合成
三角関数の合成の公式は以下のようになります。
\(a\sin\theta+b\sin\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)\)
この公式がどのように導かれたものかを説明していきます。
座標平面上の点\(P(a,b)\)を考えて、原点\(O\)と点\(P\)を結ぶ線分の長さを\(r\)、\(x\)軸と\(OP\)のなす角を\(\alpha\)とすると、下の図のようになります。
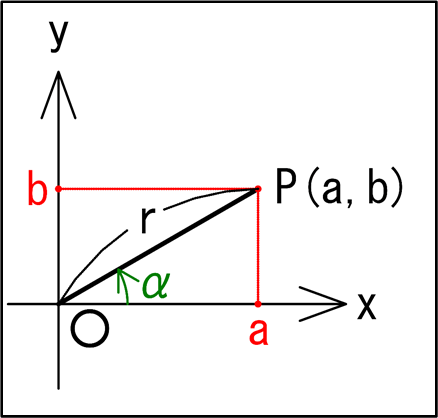
ここで直角三角形に注目すると、三平方の定理から
\(\displaystyle{\begin{eqnarray}&&r^2=a^2+b^2\\\\\Leftrightarrow&&r=\sqrt{a^2+b^2}\end{eqnarray}}\)
また、
\(a=r\sin\alpha\ \cdots①\)
\(b=r\cos\alpha\ \cdots②\)
となります。
以上から、
\(\displaystyle{\begin{eqnarray}a\sin\theta+b\cos\theta&=&r\sin\theta\cos\theta+r\cos\alpha\sin\theta\\\\&=&r(\sin\theta\cos\alpha+\cos\alpha\sin\theta)\\\\&=&r\sin(\theta+\alpha\\\\&&{(↑加法定理 \\\sin(\theta+\alpha)\\=\sin\theta\cos\alpha+\cos\alpha\sin\theta\\から)}\\\\&=&\sqrt{a^2+b^2}\sin(\theta+\alpha)\\\\&&(↑r=\sqrt{a^2+b^2}から)\end{eqnarray}}\)
となります。
また、角度\(\alpha\)の条件は、\(①と②\)から、\(r=\sqrt{a^2+b^2}\)を用いて、
\(\displaystyle{\begin{eqnarray}&&a=r\cos\alpha\\\\\Leftrightarrow&&\cos\alpha=\frac{a}{r}\\\\\Leftrightarrow&&\cos\alpha=\frac{a}{\sqrt{a^2+b^2} }(∵r=\sqrt{a^2+b^2})\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}&&b=r\sin\alpha\\\\\Leftrightarrow&&\sin\alpha=\frac{b}{r}\\\\\Leftrightarrow&&\sin\alpha=\frac{b}{\sqrt{a^2+b^2}} (∵r=\sqrt{a^2+b^2})\end{eqnarray}}\)
となります。
6.公式導出のまとめ・応用
ここまでで一通り説明してきた公式についてまとめておきます。
特に後半の公式は、加法定理から導くものが多かったと思います。
最低でも、加法定理の公式は覚えておくようにしましょう。



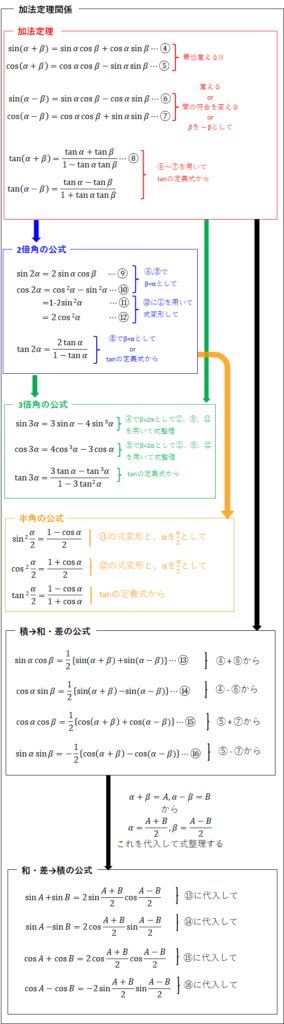
以上になります。
応用として、
\(\sin(\alpha+\beta+\gamma)\)
などの3つの角度を足した三角関数の式も、\((\beta+\gamma)=C\)などとおき、
\(\sin(\alpha+C)\)
に加法定理を用いた後、
\({\sin}C=\sin(\beta+\gamma)\)
に同様にして加法定理の式を用いると導くことができます。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


