投稿日:
【高校物理】仕事とエネルギー【仕事】【エネルギー】【エネルギー保存則】【位置エネルギー】
\(\require{color}\)
\(\require{cancel}\)
こちらの記事は、仕事とエネルギーについて解説しています。
仕事については、仕事の定義や仕事とエネルギーの等価性について解説しています。
またエネルギーについては、運動エネルギーや各種位置エネルギー、力学的エネルギーについて解説しています。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
- 1.仕事の定義
- 2.仕事の原理
- 3.仕事率
- 4.運動エネルギーと仕事の関係
- 5.重力による位置エネルギー
- 6.弾性力による位置エネルギー
- 7.保存力と非保存力
- 8.力学的エネルギー保存の法則
- 9.非保存力と力学的エネルギー
1.仕事の定義
物理における仕事の定義は、以下のようになります。
物体に力\(\vec{F}[N]\)を加え、距離\(\vec{S}[m]\)だけ移動させたとき、力\(\vec{F}\)が物体にした仕事\(W\)は、\(\vec{F}\)と\(\vec{S}\)の内積
\(\displaystyle{W=\vec{F}・\vec{S}}\)
で表されます。
また、\(\vec{F}\)と\(\vec{S}\)のなす角を\(\theta\)とすると、\(\vec{F}\)と\(\vec{S}\)の大きさ\(|\vec{F}|\)と\(|\vec{S}|\)を用いて
\(\displaystyle{\begin{eqnarray}W&=&\vec{F}・\vec{S}\\\\&=&|\vec{F}||\vec{S}|\cos\theta\end{eqnarray}}\)
とかけます。
仕事の定義式の右辺は、”(大きさ)×(大きさ)”なので、仕事はベクトルではありません。
ベクトルの内積についてはこちらも参考にしてください。
→ベクトルの内積と外積
仕事\(W\)の単位は、力\([N]\)と距離\([m]\)を掛けているので
\(N×m=N・m\)
となります。
また、\(N・m\)は別の単位でも表すことができ、この単位を\([J]\)(ジュール)といいます(新しい単位)。
\(\displaystyle{\begin{eqnarray}N・m=J\end{eqnarray}}\)
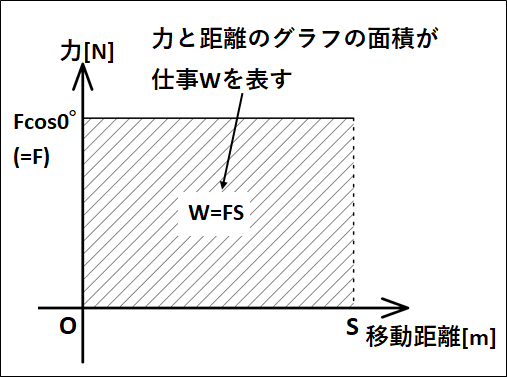
仕事は、力\(F\)と距離\(S\)のグラフの面積に相当します。
例として、下図のように物体に力\(\vec{F}[N]\)を右向きに加えて距離\(\vec{S}[m]\)だけ右向きに動かしたときに、力\(\vec{F}\)が物体にした仕事を考えてみます。
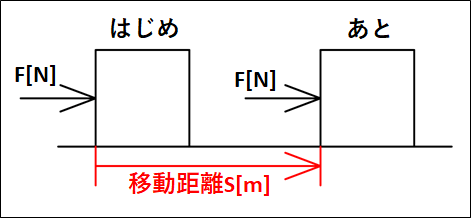
上図において、\(\vec{F}\)と\(\vec{S}\)のなす角は\(0°\)です。
また、それぞれのベクトルの大きさは\(F\)と\(S\)になります。
よって、力\(F\)が物体にする仕事\(W\)は
\(\displaystyle{\begin{eqnarray}W&=&\vec{F}・\vec{S}\\\\&=&F×S×\cos{0°}\\\\&=&FS\end{eqnarray}}\)
となります。
このときグラフは下図のようになります。
一般に、物体がいくつかの力を受けて移動する場合、それぞれの力がする仕事の和はそれらの合力がする仕事に等しくなります。
2.仕事の原理
仕事の原理とは、道具を用いて仕事をするとき、道具の質量や摩擦が無視できれば、仕事の量は道具を用いないときと変わらないという原理になります。
こちらについては、練習問題のほうで実際に問題を解きながら解説します。
3.仕事率
仕事率とは、単位時間(\(1s\))あたりにする仕事の値になります。
\(t[s]\)間の間に\(W[J]\)の仕事をするときの仕事率を\(P\)とすると、
\(\displaystyle{\begin{eqnarray}P=\frac{W[J]}{t[s]}\end{eqnarray}}\)
となります。
仕事率の単位は、仕事の単位\(J\)を時間の単位\(s\)で割っているので、\(J/s\)となります。
また、この単位\(J/s\)を別の単位\(W\)(ワット)で表すこともあります。
\(\displaystyle{J/s=W}\)
記号は\(W\)と、この記事における仕事と同じ文字になっていますが、混同しないようにしてください。
\(\bf{<考察>}\)
仕事の単位\(J\)は、力の単位\(N\)と距離の単位\(m\)を用いて、
\(J=N・m\)
と表されました。
この単位を用いて、仕事率を考えてみると
\(\displaystyle{\begin{eqnarray}{\bf{仕事率}}([W=J/s])&=&\frac{\bf{仕事[J]}}{\bf{時間[s]}}\\\\&=&\frac{\bf{力[N]}×距離[m]}{時間[s]}\end{eqnarray}}\)
ここで、分子の距離\(m\)と分母の時間\(s\)に注目すると、これは
\(\displaystyle{\frac{距離[m]}{時間[s]}=速さ[m/s]}\)
となります。
これを用いると、仕事率は下記のようにも表すことができます。
\(\displaystyle{\begin{eqnarray}{\bf{仕事率}}([W=J/s])&=&\frac{\bf{仕事[J]}}{\bf{時間[s]}}\\\\&=&\frac{\bf{力[N]}×距離[m]}{時間[s]}\\\\&=&\textcolor{red}{\bf{力[N]×速さ[m/s]}}\end{eqnarray}}\)

4.運動エネルギーと仕事の関係
物体が仕事をする能力をもっているとき、この物体は”エネルギーをもつ”といいます。
運動する物体がもつ仕事する能力を\(\textcolor{red}{\bf{運動エネルギー}}\)といい、質量\(m[kg]\)の物体が速さ\(v[m/s]\)で運動しているときの運動エネルギー\(K\)は、
\(\displaystyle{K=\frac{1}{2}mv^2}\)
で表されます。
単位は、\(N=kg・m/s^2\)なので
\(\displaystyle{\begin{eqnarray}kg×(m/s)^2&=&kg・m/s^2×m\\\\&=&N・m\\\\&=&J\end{eqnarray}}\)
のように、(J)(ジュール)となり、仕事の単位と同じになります。
また、物体の運動エネルギーと物体にはたらいている力がした仕事の間には、以下のような関係があります。
\(\displaystyle{\textcolor{red}{\frac{1}{2}mv^2_{あと}-\frac{1}{2}mv^2_{はじめ}=W_1+W_2+W_3+\cdots}}\)
\(v_{あと}\)は物体のあとの速度、\(v_{はじめ}\)は物体のはじめの速度となります。
上記の式の右辺は、運動エネルギーの(あと-はじめ)、すなわち運動エネルギーの変化量を表しています。
上式の右辺は、物体にはたらいている力がした仕事の和になります。
これを、言葉で表すと
(運動エネルギーの変化量)=(仕事の和)
となります。
これを、
\(\textcolor{red}{\bf{運動エネルギーと仕事の(等価性)原理}}\)
といいます。
上式は、\(\textcolor{red}{\bf{覚えておく必要があります}}\)。
“運動エネルギーと仕事の原理”を考えるために、複数の力がかかっている物体を考えます。
少しだけ微積を用いるので、興味がない方は飛ばしてもらってもかまいませんが、上式の”運動エネルギーと仕事の原理”の式は覚えておきましょう。
力は、3つだけ図示してありますが、複数かかっているとしています。
また、この力がはたらいている状態で初速度\(v_{はじめ}\)を物体に与え、\(\vec{r}\)だけ移動したあとの物体の速度を\(v_{あと}\)としています。
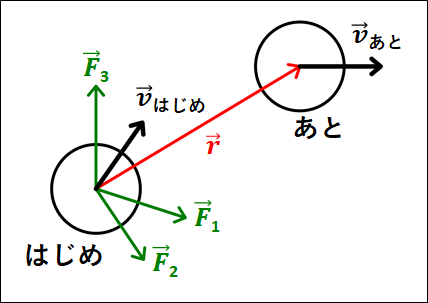
上図の状態において、物体の運動方程式は、
\(\displaystyle{m\vec{a}=\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots}\)
となります。
上記の運動方程式の両辺に\(\vec{v}\)を内積して、計算していくと下図のようになります。

仕事率の部分で考察したように、(力×速度)は仕事率となります。
次に、合成関数の微分法を用いて、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}v^2&=&\frac{dv^2}{dv}\frac{dv}{dt}\\\\&=&2v\frac{dv}{dt}\end{eqnarray}}\)
から、
\(\displaystyle{v\frac{dv}{dt}=\frac{d}{dt}\frac{1}{2}v^2}\)
※合成関数の微分については、こちらを参考にしてください。
→微分法とその応用
これを用いて、式変形を続けていくと、

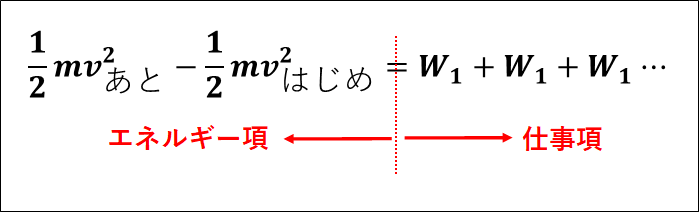
以上より、上式の分子\(d\left\{\right\}\)のみを考えると、\(\textcolor{red}{d}\)は\(\textcolor{red}{\bf{あと-はじめ}}\)という意味なので、
\(\displaystyle{\frac{1}{2}mv^2_{あと}-\frac{1}{2}mv^2_{はじめ}=W_1+W_2+W_3+\cdots}\)
となります。
はじめの位置では、物体は移動していないのではじめの仕事はすべてゼロとなります。
また、\(\vec{v}\)は2乗されているので、これはベクトルではなくベクトルの”大きさ”となります。
ここで、もう一度”運動エネルギーと仕事の原理”の式の意味を確認しておきます。

上式は、
“物体の運動エネルギーの変化は、その物体がされた仕事に等しい”
ことを示しています。
また、左辺を”エネルギー項”、右辺を”仕事項”といいます。
また、エネルギー積分についても触れておきます。
これは、電磁気の分野でも扱います。
\(\bf{\underline{○エネルギー積分}}\)
直線上の運動(今回は\(x\)軸上)を考えます。
運動方程式は、
\(\displaystyle{ma=F}\)
両辺に\(v\)を掛けて
\(\displaystyle{\begin{eqnarray}&&mva=Fv\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=F\frac{dx}{dt} \left(∵a=\frac{dv}{dt} , v=\frac{dx}{dt}\right)\end{eqnarray}}\)
ここで、両辺\(t\)で\(t_{はじめ}{\to}t_{あと}\)まで積分して、
\(\displaystyle{\int_{t_{はじめ}}^{t{あと}}{mv\frac{dv}{dt}}dt=\int_{t_{はじめ}}^{t{あと}}{F\frac{dx}{dt}}dt}\)
\(x\)と\(v\)は\(t\)の関数なので、\(t_{はじめ}{\to}t_{あと}\)のとき\(x_{はじめ}{\to}x_{あと}\)、\(v_{はじめ}{\to}v_{あと}\)であるとすると、
\(\displaystyle{\begin{eqnarray}&&\int_{v_{はじめ}}^{v_{あと}}{mv}dv=\int_{x_{はじめ}}^{x_{あと}}{F}dx\\\\{\Leftrightarrow}&&\left[\frac{1}{2}mv^2\right]_{v_{はじめ}}^{v_{あと}}=\int_{x_{はじめ}}^{x_{あと}}{F}dx\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\int_{x_{はじめ}}^{x_{あと}}{F}dx\end{eqnarray}}\)
となります。

5.重力による位置エネルギー
物体に重力がはたらいているとき、重力がした仕事を\(W_{mg}\)とすると、運動エネルギーと仕事の等価性から、
\(\displaystyle{\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\textcolor{green}{W_{mg}}}\)
となります。
上式のおいて、重力がした仕事\(W_{mg}\)をエネルギー項である左辺に移項したもの、つまり\(-W_{mg}\)が”重力による位置エネルギーの変化量”となります。
位置エネルギーにも、運動エネルギーと同様に”はじめの位置エネルギー”と”あとの位置エネルギー”があります。
なので、位置エネルギーの変化量だけを扱う場合には\(-W_{mg}\)を用いればよいですが、”はじめの重力による位置エネルギー”と”あとの重力による位置エネルギー”をそれぞれ扱う場合には、\(\textcolor{green}{\bf{基準面}}\)を決めて、\(\textcolor{green}{\bf{座標}}\)で考える必要があります。
例をみていきましょう。
例)
基準面\(O\)から高さ\(h\)だけ高い位置\(P\)にある質量\(m\)の物体を静かに落とした場合について。
状況は下図のようになります。
“高さ”といわれたときには、上向きを正とします。
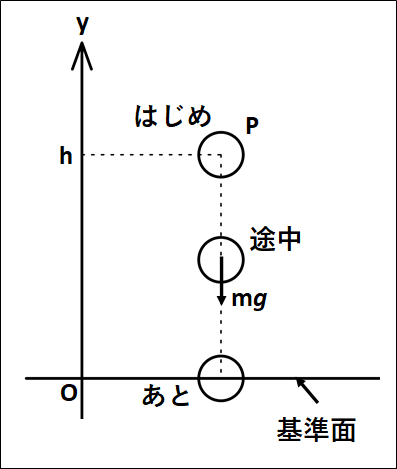
物体が\(P\)から\(O\)まで移動するとき、運動エネルギーと仕事の等価性から
\(\displaystyle{\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_{mg}}\)
ここで、重力は鉛直下向きに大きさ\(mg\)で、移動距離は下向きに\(h\)だけ移動しています。
この重力と移動距離のベクトルのなす角は\(0°\)となるので、重力がした仕事は
\(\displaystyle{\begin{eqnarray}W_{mg}&=&mg×h×\cos{0°}\\\\&=&mgh\end{eqnarray}}\)
となります。
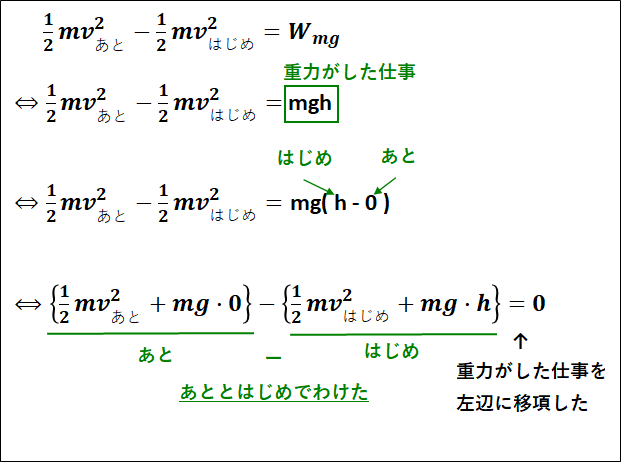
また、これを座標で捉えると、
\(\displaystyle{mgh=mg(h-0)}\)
となります。
これらを用いて、式を変形していくと下図のようになります。
上式において、

運動エネルギーを\(K\)と表しましたが、位置エネルギーは\(U\)と表します。
上式の結果から、基準面から高さ\(h\)だけ高い位置にある物体の重力による位置エネルギー\(U\)は\(mgh\)となります。
(はじめ(点P)の重力による位置エネルギー)
(基準面にある物体の重力による位置エネルギーは\(0\))
※
重力がする仕事について、途中の運動方程式を考えると上向きを正としているので
\(ma=-mg\)
これより、重力と距離のグラフを考えると、その面積が重力がした仕事となるので下図のようになります。
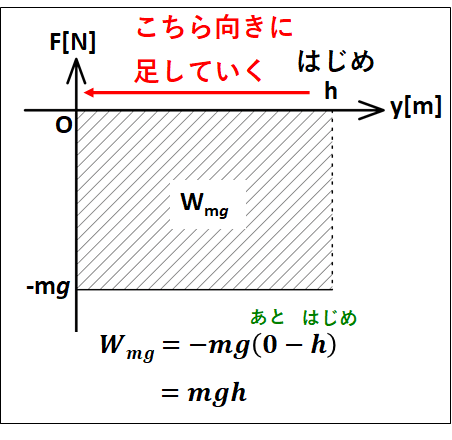
物理においては、面積の符合も意味をもつので、力の正負や足していく向きも考える必要があります。
これを積分で表すと、
\(\displaystyle{\begin{eqnarray}\int_h^0{(-mg)}dy&=&\left[-mgy\right]_h^0\\\\&=&-mg・0-(-mg)・h\\\\&=&mgh\end{eqnarray}}\)
となります。
また、重力がした仕事は物体の移動経路が曲線や斜めの場合でも、重力の大きさと物体が鉛直方向に動いた距離で決まります。
このことについては、練習問題で取り扱います。
6.弾性力による位置エネルギー
物体に弾性力がはたらいているとき、弾性力がした仕事を\(W_{s}\)とすると、運動エネルギーと仕事の等価性から、
\(\displaystyle{\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\textcolor{green}{W_{s}}}\)
となります。
上式のおいて、弾性力がした仕事\(W_{s}\)をエネルギー項である左辺に移項したもの、つまり\(-W_{s}\)が”弾性力による位置エネルギーの変化量”となります。
こちらも重力による位置エネルギーと同様に、”はじめの位置エネルギー”と”あとの位置エネルギー”を考える際には、座標を用います。
例をみていきます。
例)
自然長の位置を原点として、原点から\(L[m]\)だけ伸びたバネにつながれた物体が、自然長にもどるときを考える。
(ばね定数を\(k\)とし、ばねが伸びる方向に\(x\)軸をとる)
床はなめらかであるとします。
状況は下図のようになります。
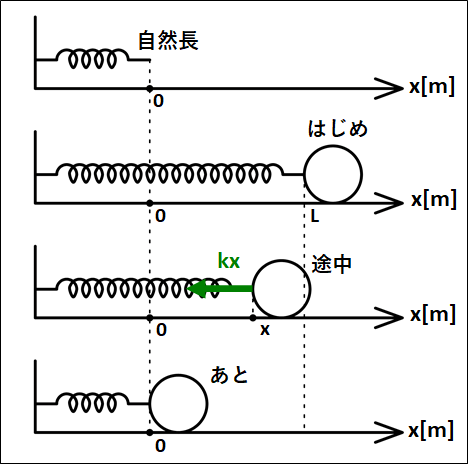
途中での物体の位置を\(x\)としています。
物体が運動している途中での運動方程式は、軸を右向き正にとっているので、ばねによる弾性力が負の方向にかかっていることから、
\(ma=-kx\)
これをもとにして、弾性力と位置のグラフを描くと次のようになります。
グラフと一緒に、自然長、はじめの位置、あとの位置の物体も一緒に載せておきます。
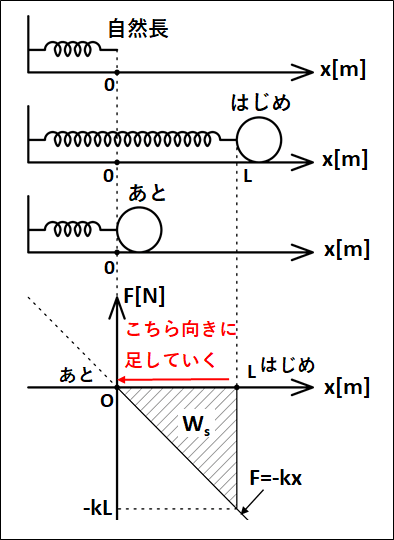
グラフの面積が、弾性力のした仕事なので、三角形の面積を求める式から、
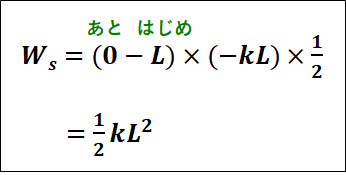
※
積分を用いると、
\(\displaystyle{\begin{eqnarray}\int_L^0{(-kx)}dx&=&\left[-\frac{1}{2}lx^2\right]_L^0\\\\&=&-\frac{1}{2}k・0^2-\left(-\frac{1}{2}kL^2\right)\\\\&=&\frac{1}{2}kL^2\end{eqnarray}}\)
となります。
以上より、ばねの弾性力がした仕事が求まったので、重力による位置エネルギーのときと同様にして、運動エネルギーと仕事の原理から、式変形をしていくと下図のようになります。
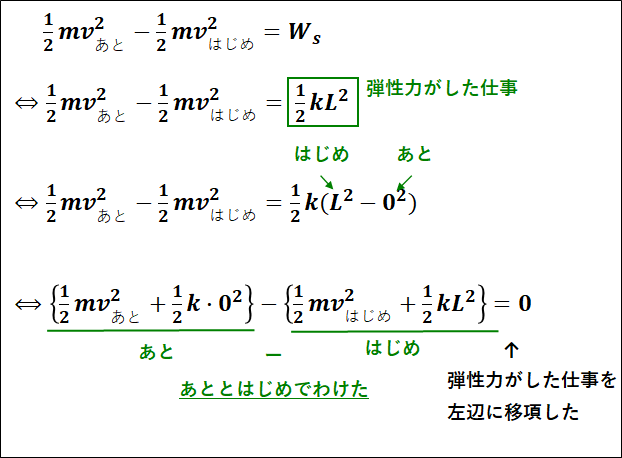
上式において、

上式の結果から、自然長から\(L\)だけ伸びたばねの弾性力による位置エネルギー\(U\)は、ばねの自然長の位置を基準にとると
\(\displaystyle{U=\frac{1}{2}kL^2}\)
となります。
(はじめの弾性力による位置エネルギー)
(自然長でのばねの弾性力による位置エネルギーは\(0\))
7.保存力と非保存力
\(\textcolor{red}{\bf{保存力}}\)とは、”力がする仕事が途中の経路によらず、はじめとあとの2点(はじめの位置とあとの位置)だけで決まる力”のこととなります。
\(\textcolor{red}{\underline{\bf{○代表的な保存力:}}}\)
\(\textcolor{red}{\bf{重力、万有引力、弾性力、静電気力(クーロン力)}}\)
\(\textcolor{red}{\bf{非保存力}}\)とは、”力がする仕事が、はじめとあとの位置だけでは決まらずに、経路によるもの”となります。
例としては、摩擦力や空気抵抗などがあります。
“保存力”と”非保存力”については、”保存力”を覚えておきましょう。
保存力でないものは、非保存力となります。
また、運動エネルギーと仕事の等価性原理の式から、仕事を仕事項からエネルギー項へ移項した際に「○○による位置エネルギー」となるのは”保存力”のみとなります。
(非保存力は、移行させても位置エネルギーにならない(はじめとあとだけで決まらない))
保存力と非保存力の例として、重力と摩擦力を比較してみます。
例)
\(\bf{\underline{保存力:重力}}\)
質量\(m\)の物体が下図のように、\(A→B→C\)と移動するときの重力がした仕事を考えます。
\(A\)点を基準として、\(A\)から\(B\)までの距離を\(l_1\)、\(A\)から\(C\)までの距離を\(l_2\)とします。
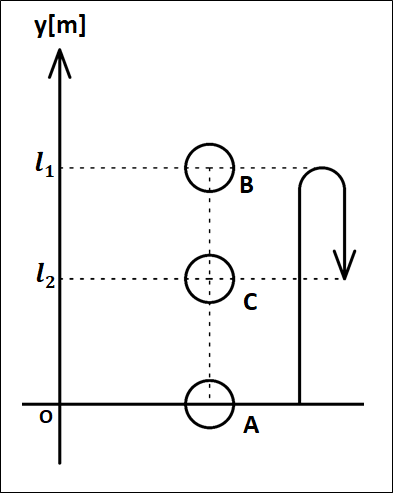
重力\(mg\)は常に鉛直下向きにかかっています。
\(\bf{\underline{・A→B間}}\)
上向きに\(l_1\)だけ移動します。
よって、重力とはなす角が\(180°\)になるので、この間に重力がした仕事は
\(\displaystyle{mg×l_1×\cos{180°}=-mgl_1}\)
\(\bf{\underline{・B→C間}}\)
下向きに\((l_1-l_2)\)だけ移動します。
重力とのなす角は\(0°\)なので、この間に重力がした仕事は
\(\displaystyle{mg×(l_1-l_2)×\cos{0°}=mg(l_1-l_2)}\)
\(\bf{\underline{・全体でした仕事}}\)
全体でした仕事は、\(A→B\)の間にした仕事と\(B→C\)の間にした仕事を足して、
\(\displaystyle{\begin{eqnarray}-mgl_1+mg(l_1-l_2)&=&-mg(l_1-l_1+l_2)\\\\&=&-mg(l_2-0)\end{eqnarray}}\)
これより、保存力である重力がした仕事は、はじめの位置である\(0\)とあとの位置である\(l_2\)のみで決まり、途中の位置\(l_1\)は関係ないことが分かります。

例)
\(\bf{\underline{非保存力:摩擦力}}\)
物体が下図のように、\(A→B→C\)と移動するときの摩擦力がした仕事を考えます。
\(A\)点を基準として、\(A\)から\(B\)までの距離を\(l_1\)、\(A\)から\(C\)までの距離を\(l_2\)とします。
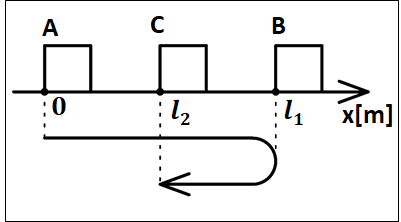
かかっている動摩擦力の大きさを\(f\)とします。
この摩擦力は、”物体が運動する向きと反対向き”にはたらきます。
\(\bf{\underline{・A→B間}}\)
右向きに\(l_1\)だけ移動します。
摩擦力\(f\)は物体が運動する向きと逆向きの左向きにかかります。
よって、2つのベクトルのなす角は\(180°\)となるので、この間で摩擦力がした仕事は
\(\displaystyle{f×l_1×\cos{180°}=-fl_1}\)
\(\bf{\underline{・B→C間}}\)
左向きに\((l_1-l_2)\)だけ移動します。
摩擦力\(f\)は物体が運動する向きと逆向きの右向きにかかります。
よって、2つのベクトルのなす角は\(180°\)となるので、この間で摩擦力がした仕事は
\(\displaystyle{f×(l_1-l_2)×\cos{180°}=-f(l_1-l_2)}\)
\(\bf{\underline{・全体でした仕事}}\)
全体でした仕事は、\(A→B\)の間にした仕事と\(B→C\)の間にした仕事を足して、
\(\displaystyle{\begin{eqnarray}-fl_1-f(l_1-l_2)&=&-f(l_1+l_1-l_2)\\\\&=&-f(2l_1-l_2)\end{eqnarray}}\)
上式から、非保存力である摩擦力がした仕事は、はじめとあとの位置だけでは決まらず、途中の位置も考えなければならないことがわかります。

8.力学的エネルギー保存の法則
\(\textcolor{red}{力学的エネルギー}\)とは、”運動エネルギーと位置エネルギーの和”のことです。
すなわち、運動エネルギーを\(K\)、位置エネルギーを\(U\)とすると、
\(\textcolor{red}{{\bf{力学的エネルギー}}=K+U}\)
となります。
\(\textcolor{red}{\bf{力学的エネルギー保存の法則}}\)とは、
“物体が保存力\(\textcolor{red}{\bf{だけ}}\)から\(\textcolor{green}{\bf{仕事}}\)をされるとき、運動エネルギーと位置エネルギーの和である力学的エネルギーは保存される”
という法則です。
保存するとは、”はじめの力学的エネルギー”と”あとの力学的エネルギー”が等しいということです。
また言い換えると、力学的エネルギーの変化量が”ゼロ”だということです。
式で表すと、運動エネルギーを\(K\)、位置エネルギーを\(U\)、変化量を表す\(\Delta\)を用いると
\(\displaystyle{\begin{eqnarray}&&(K_{あと}+U_{あと})=(K_{はじめ}+U_{はじめ})\\\\{\Leftrightarrow}&&(K_{あと}+U_{あと})-(K_{はじめ}+U_{はじめ})=0\\\\{\Leftrightarrow}&&\Delta(K+U)=0\end{eqnarray}}\)
となります。
ただし、これが成り立つのは”物体が保存力だけから仕事をされるとき”という条件が必要となります。
(非保存力による仕事は、エネルギー項に移項させても位置エネルギーとはならない)
“保存力だけから仕事をされるとき”なので、物体に非保存力がはたらいていても、その非保存力がした仕事が”ゼロ”であれば”力学的エネルギー保存の法則”は成り立ちます。
(個人的には、力学的エネルギーの法則は、運動エネルギーと仕事のと原理から自然に導かれるので、覚える必要はないと思いますが…)
これから、いくつか例をみていきます。
例1)
なめらかな斜面上を、斜面に沿って高さ\(h_A\)から\(h_B\)まで滑り降りる質量\(m\)の物体
状況は下図のようになります。
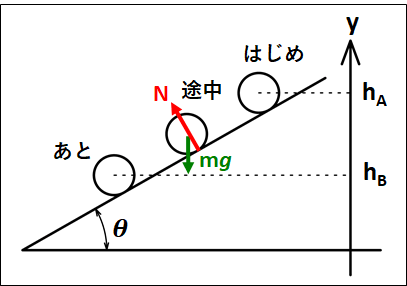
途中でかかっている力は、鉛直下向きに重力\(mg\)と、斜面と直角に垂直抗力\(N\)がかかっています。
運動エネルギーと仕事の原理から、重力がした仕事を\(W_{mg}\)、垂直抗力がした仕事を\(W_{N}\)とすると、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_{mg}+W_{N}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=mg(h_A-h_B)+N×\frac{h_A-h_B}{\sin\theta}\cos{90°}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=mg(h_A-h_B)+0\end{eqnarray}}}\)
上式をさらに式変形していくと、下図のようになります。

上式のように、物体に非保存力である垂直抗力がはたらいていますが、その仕事は”ゼロ”となっているので、力学的エネルギーは保存しています。
※重力がした仕事、\(W_{mg}=mg(h_A-h_B)\)に関して、下図を考えます。
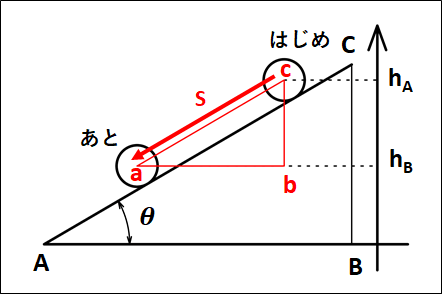
下図において、物体が移動した距離を\(s\)としています。
物体は、斜面に沿って移動するので、
\(AC//ac\)
です。
また、\(ac\)を斜辺とする直角三角形を考えているので、
\(AB//ab\)、\(BC//bc\)
です。
これより、
\(\angle{BAC}=\angle{bac}=\theta\)
\(\angle{ABC}=\angle{abc}=90°\)
\(\angle{ACB}=\angle{acb}=90°-\theta\)
となり、下図のようになります。
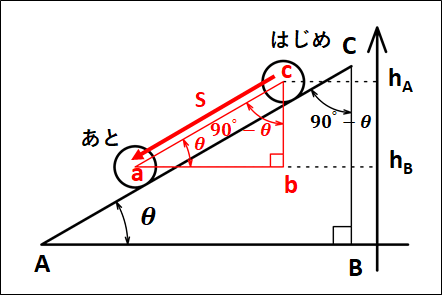
ここで、重力がした仕事は仕事の定義から
\(\displaystyle{\begin{eqnarray}W_{mg}&=&mg×s×\cos(90°-\theta)\\\\&=&mg×s×\sin\theta\end{eqnarray}}\)
三角関数から、\(s\sin\theta\)は\(h_A-h_B\)なので、重力がした仕事は
\(\displaystyle{\begin{eqnarray}W_{mg}&=&mg×s×\sin\theta\\\\&=&mg(h_A-h_B)\end{eqnarray}}\)
となります。
※三角関数についてはこちら
→三角関数の定義と関係式
→三角関数の公式
一般的に、重力がした仕事は重力の大きさと高さだけで決まってきます。
これについては、練習問題で詳しく扱っています。
例2)
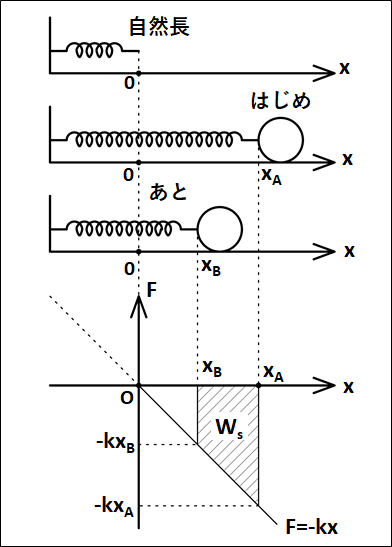
なめらかな平面上で、ばねにつながれた質量\(m\)の物体が自然長からの伸び\(x_A\)から\(x_B\)まで移動するとき。
ばね定数を\(k\)とする。
途中でかかっている力は、以下のようになります。
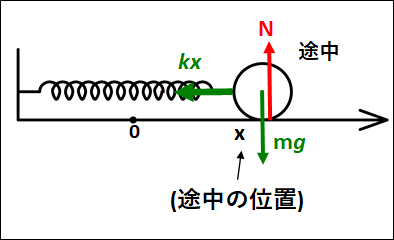
かかっている力は、重力\(mg\)と垂直抗力\(N\)と弾性力\(kx\)になります。
なので、仕事もこれら3つの力による仕事を考えなけばなりません。
弾性力による仕事\(W_s\)についてですが、上図の面積となるので、あとの負の面積(小さい三角形)からはじめの負の面積(大きい三角形)を引いて
\(\displaystyle{\begin{eqnarray}W_s&=&-\frac{1}{2}kx_B^2-\left\{-\frac{1}{2}kx_A^2\right\}\\\\&=&\frac{1}{2}k(x_A^2-x_B^2)\end{eqnarray}}\)
※
積分表示は\(\displaystyle{\int_{x_A}^{x_B}{-kx}dx}\)
以上から、弾性力による仕事を\(W_s\)、垂直抗力による仕事を\(W_N\)、重力による仕事を\(W_{mg}\)とすると、これまでと同様に運動エネルギーと仕事の原理から
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_s+S_N+W_{mg}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(x_A^2-x_B^2)+N(x_A-x_B)\cos{90°}\\&& +mg(x_A-x_B)\cos{90°}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(x_A^2-x_B^2)+0+0\end{eqnarray}}}\)
上式をさらに式変形していくと、下図のようになります。

上式より、力学的エネルギーである”運動エネルギー”と”弾性力による位置エネルギー”の和は保存しています。
例3)
ばねで吊り下げられた質量\(m\)の物体が、自然長からの伸びが\(y_A\)から\(y_B\)まで移動するとき。
ばね定数を\(k\)とする。
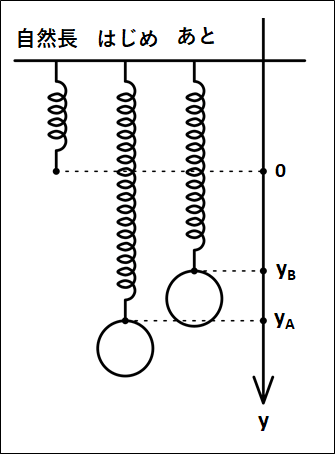
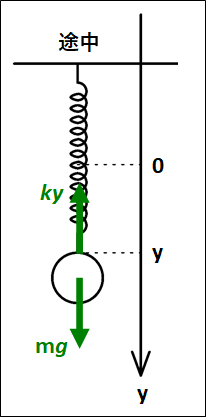
途中の位置\(y\)でかかっている力は、以下のようになります。
今回は、自然長の位置を原点としていますが、つりあいの位置を原点にすることもあります。
(特に、単振動の分野で)
物体にかかっている力は、鉛直下向きに重力\(mg\)と鉛直上向きに弾性力\(ky\)、また進んだ距離は上向きに\(y_A-y_B\)となります。
以上から、これまでと同様に運動エネルギーと仕事の原理から、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=W_s+W_{mg}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(y_A^2-y_B^2)-mg(y_A-y_B)\end{eqnarray}}}\)
上式をさらに式変形していくと、下図のようになります。

上式より、力学的エネルギーである”運動エネルギー”と”弾性力による位置エネルギー”と”重力による位置エネルギー”の和は保存しています。
※
大学的に…
例3の途中の運動方程式は、
\(ma=mg-ky\)
上式の両辺に\(v\)をかけて
\(\displaystyle{\scriptsize{\begin{eqnarray}&&mva=mgv-ky・y\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=mg\frac{dy}{dt}-ky\frac{dy}{dt} \cdots①\\\\{\Leftrightarrow}&&\int_{t_{はじめ}}^{t_{あと}}{mv\frac{dv}{dt}}dt=\int_{t_{はじめ}}^{t_{あと}}{mg\frac{dy}{dt}}dt+\int_{t_{はじめ}}^{t_{あと}}{-ky\frac{dy}{dt}}dt\end{eqnarray}}}\)
ここで、\(t_{はじめ}→t_{あと}\)のとき、\(v_{はじめ}→v_{あと}\)、\(y_{A}→y_{B}\)とすると、
\(\displaystyle{\scriptsize{\begin{eqnarray}&&\int_{v_{はじめ}}^{v_{あと}}mvdv=\int_{y_A}^{y_B}mgdy+\int_{y_A}^{y_B}(-ky)dy\\\\{\Leftrightarrow}&&\left[\frac{1}{2}mv^2\right]_{v_{はじめ}}^{v_{あと}}=\left[mgy\right]_{y_A}^{y_B}+\left[\frac{1}{2}ky^2\right]_{y_A}^{y_B}\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=mg(y_B-y_A)-\frac{1}{2}k(y_B^2-y_A^2)\\\\{\Leftrightarrow}&&\frac{1}{2}mv_{あと}^2-\frac{1}{2}mv_{はじめ}^2=\frac{1}{2}k(y_A^2-y_B^2)-mg(y_A-y_B)\end{eqnarray}}}\)
となり、例3でみた式と同じになります。
また、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\left(\frac{1}{2}mv^2\right)&=&\frac{dv}{dt}・\frac{d}{dv}\left(\frac{1}{2}mv^2\right)\\\\&=&mv\frac{dv}{dt}\end{eqnarray}}\)
\(\displaystyle{\frac{dy}{dt}・\frac{d}{dy}(mgy)=mg\frac{dy}{dt}}\)
\(\displaystyle{\frac{dy}{dt}・\frac{d}{dy}\left(\frac{1}{2}ky^2\right)=ky\frac{dy}{dt}}\)
から、これらを①式に用いると、
\(\displaystyle{\begin{eqnarray}&&mv\frac{dv}{dt}=mg\frac{dy}{dt}-ky\frac{dy}{dt}\\\\{\Leftrightarrow}&&\frac{d}{dt}\left(\frac{1}{2}mv^2\right)=\frac{d}{dt}(mgy)-\frac{d}{dt}\left(\frac{1}{2}ky^2\right)\\\\{\Leftrightarrow}&&\frac{d}{dt}\left\{\frac{1}{2}mv^2+\frac{1}{2}ky^2-mgy\right\}=0\end{eqnarray}}\)
上記の式は、{}内の式を時間\(t\)で微分すると\(0\)になるということを表しています。
すなわち、{}内の部分は定数であり、これは時間(t)を含まないので時間に依存しません。
なので、{}内は定数であり、どの時間においても一定の値なので
はじめ:
\(\displaystyle{\frac{1}{2}mv_{はじめ}^2+\frac{1}{2}ky_A^2-mgy_A=K}\)
あと:
\(\displaystyle{\frac{1}{2}mv_{あと}^2+\frac{1}{2}ky_B^2-mgy_B=K}\)
となり、上記2つの式の値は等しいので
\(\displaystyle{\scriptsize{\frac{1}{2}mv_{あと}^2+\frac{1}{2}ky_B^2-mgy_B=\frac{1}{2}mv_{はじめ}^2+\frac{1}{2}ky_A^2-mgy_A}}\)
が成り立つ、すなわち力学的エネルギー保存の法則が成り立ちます。
9.非保存力と力学的エネルギー
保存力である重力について、物体を初速度\(v_0\)で真上に投げた際、最高点\(h\)をあとの位置とすると、運動エネルギーと仕事の原理から
\(\displaystyle{\begin{eqnarray}&&\frac{1}{2}m・0^2-\frac{1}{2}mv_0^2=-mgh\\\\{\Leftrightarrow}&&\frac{1}{2}mv_0^2=mgh\end{eqnarray}}\)
となります。
物体は最高点に達してから一瞬静止しても、落下してもとの高さに戻るときには速さ\(v_0\)となります。
このことから、高さ\(h\)にある物体は、\(mgh\)の仕事をする能力をもっており、これを用いて運動エネルギーを生み出す能力をもっています。
しかし、非保存力である摩擦力については、一度止まってしまうと、自発的に動き出すことはなく運動エネルギーを生み出す能力をもっていません。
よって、はじめの運動エネルギーは回復されずに失われたままとなってしまいます(保存しない)。
一般的に、物体が保存力以外の力から仕事をされると、物体の力学的エネルギーはその分だけ変化し保存しません。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


