投稿日:
【高校物理】三角関数①/定義と関係式【高校数学】【三角関数】
\(\require{color}\)
\(\require{cancel}\)
三角関数では、\(\sin\)(サイン)、\(\cos\)(コサイン)、\(\tan\)(タンジェント)を用います。
この三角関数の定義は、直角三角形によるものと単位円によるものがあります。
ここで、2辺がなす角度も関係してくるのですが、直角三角形における定義では、直角三角形が成り立たなければならないので角度を\(\theta\)とするとその範囲は、
\(0°\lt\theta\lt90°\)
となります。
一方単位円による定義では全ての範囲の角度で定義することができます。
この記事では、この直角三角形による定義と単位円による定義、そしてこれらの間に成り立つ関係式について解説していきます。
定理や公式は導き出すことができるので最悪覚えなくてもよいですが、今回は定義についての話なので覚えなければなりません。
物理においては、力の分解や単振動、電磁気分野で用います。
三角関数に関する記事は、こちらも参考にしてください。
→三角関数のグラフ
→三角関数の公式
→練習問題1(定義とグラフ)
→練習問題2(三角方程式と公式)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.直角三角形による三角関数の定義
1-1.直角三角形による定義
直角三角形による三角関数の定義は、\(0°\lt\theta\lt90°\)の範囲で下図直角三角形\(\mathrm{ABC}\)において、
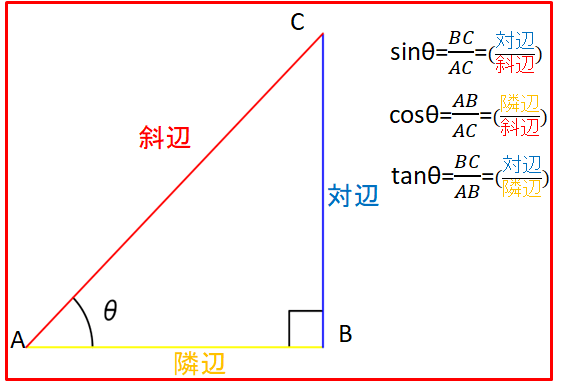
これが直角三角形における\(\sin\theta\)、\(\cos\theta\)、\(\tan\theta\)の定義となります。
\(\theta\)は直角の向かい側の角度で、\(\theta\)に接している斜めの辺\(\mathrm{\textcolor{red}{AC}}\)を\(\bf{\textcolor{red}{“斜辺”}}\)、 \(\bf{\textcolor{red}{斜辺}}\) とは異なる\(\theta\)にへばりついている辺\(\mathrm{\textcolor{#ffd700}{AB}}\)を\(\bf{\textcolor{#ffd700}{“隣辺”}}\)、\(\theta\)の向かい側の辺\(\mathrm{\textcolor{blue}{BC}}\)を\(\bf{\textcolor{blue}{“対辺”}}\)といいます。
また、上式から斜辺\(\mathrm{AB}\)の値を\(\mathrm{AB=r}\)とすると、
\(\displaystyle{\begin{eqnarray}&&\sin\theta=\mathrm{\frac{BC}{r}}\\\Leftrightarrow&&\mathrm{BC}=r\sin\theta\end{eqnarray}}\)
これより、
\(\bf{\textcolor{red}{(\thetaの向かい側の辺)=”斜辺×\sin\theta”}}\)
また、
\(\displaystyle{\begin{eqnarray}&&\cos\theta=\mathrm{\frac{AB}{r}}\\\Leftrightarrow&&\mathrm{AB}=r\cos\theta\end{eqnarray}}\)
これより、
\(\bf{\textcolor{red}{(\thetaにへばりついている辺)=”斜辺×\cos\theta”}}\)
以上から、\(\textcolor{red}{\bf{斜辺}}\)と\(\theta\)の値が分かれば、\(\textcolor{blue}{\bf{“対辺\mathrm{BC}”}}\)と\(\textcolor{#ffd700}{\bf{“隣辺\mathrm{AB}”}}\)の値が計算できることが分かります。
1-2.有名角の辺の比
直角三角形による定義でみたように、各三角関数は辺の比で決まりますが、角度\(\theta\)が\(\mathrm{30°,45°,60°}\)のときの辺の比はよくでてくるので覚えておく必要があります。
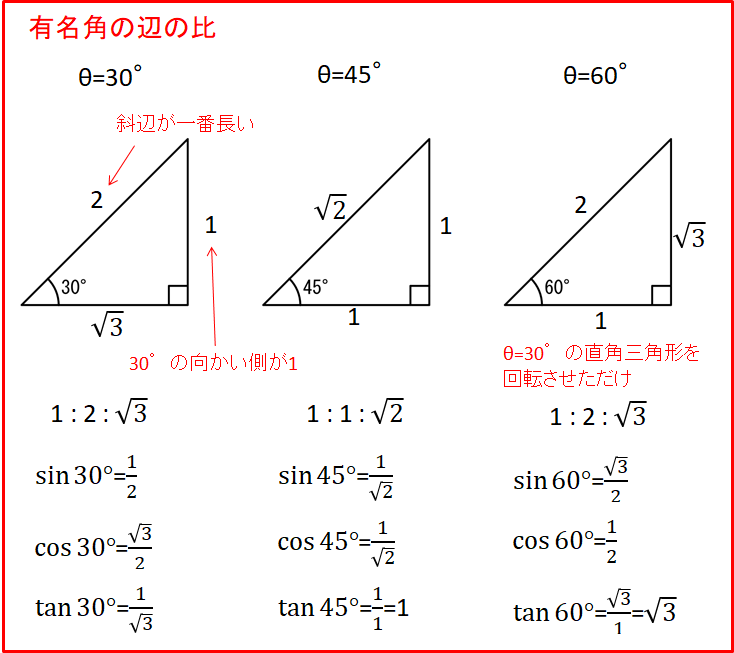
このように、角度が\(\theta\)が\(\mathrm{30°,45°,60°}\)のときと三角関数の値は上記のようになります。
ここで注意してもらいたいのが、これらは辺の比であるということです。
辺の比なので、相似な三角形を考えた場合では辺の長さは異なりますが、辺の比は同じとなります。
例として下図のような辺の長さをもつ三角形を考えてみます。
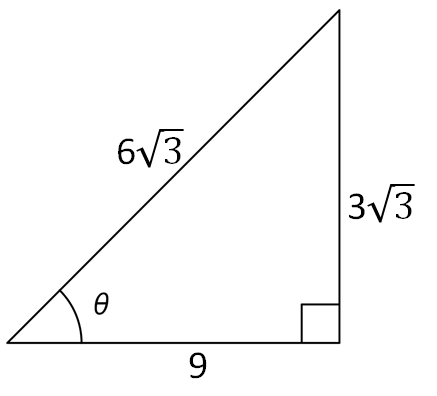
辺の長さ自体は、\(\textcolor{blue}{\bf{“対辺”}}\)=\(\mathrm{3\sqrt{3}}\)、\(\textcolor{red}{\bf{“斜辺”}}\)=\(\mathrm{6\sqrt{3}}\)、\(\textcolor{#ffd700}{\bf{“隣辺”}}\)=\(\mathrm{9}\)ですが、辺の比を考えてみると、
\(\displaystyle{\bf{\textcolor{blue}{“対辺”} : \textcolor{red}{“斜辺”} : \textcolor{#ffd700}{“隣辺”}}=\mathrm{3\sqrt{3}:6\sqrt{3}:9}}\)
各辺を\(\mathrm{3\sqrt{3}}\)で割ると、
\(\displaystyle{\mathrm{3\sqrt{3}:6\sqrt{3}:9=1:2:\sqrt{3}}}\)
となり、\(\theta=30°\)のときと同様の辺の比となり、逆に、辺の比から角度が\(\mathrm{30°}\)であることもわかります。
三角関数自体も辺の比を扱っているので、
\(\displaystyle{\begin{eqnarray}\mathrm{\sin{30°}}&=&\mathrm{\frac{3\sqrt{3}}{6\sqrt{3}}}\\&=&\mathrm{\frac{1}{2}←(3\sqrt{3}で約分した)}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\mathrm{\cos{30°}}&=&\mathrm{\frac{9}{6\sqrt{3}}}\\&=&\mathrm{\frac{\sqrt{3}}{2}←(3\sqrt{3}で約分した)}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\mathrm{\tan{30°}}&=&\mathrm{\frac{3\sqrt{3}}{9}}\\&=&\mathrm{\frac{1}{\sqrt{3}}←(3\sqrt{3}で約分した)}\end{eqnarray}}\)
というように、\(\theta=30°\)のときと同じ値になります。
1-3.新たな角度の単位[rad](ラジアン)
これまでは、角度の単位として°(度)を用いてきましたが、ここで新しい単位として(rad)(ラジアン)がでてきます。
度とラジアンの関係は以下のようになります。
\(180°={\pi} rad\)
この関係式を両辺(180°)で割ると、
\(1=\frac{{\pi}rad}{180°}=\frac{\pi}{180}rad/°\)
という関係式が得られます。
この式から、°(度)をrad(ラジアン)に変換することができます。
単位の話についてはこちらも参考にしてください
→単位の計算や換算方法
下記にいくつか例を載せておきます。
例)
\(\displaystyle{\begin{eqnarray}30^{\circ}&=&30^{\circ}×\textcolor{red}{1}\\&=&30^{\circ}×\textcolor{red}{\frac{\pi}{180}rad^{/\circ}}\\&=&\frac{30\pi}{180}\frac{rad\cdot\textcolor{blue}{\cancel{^{\circ}}}}{\textcolor{blue}{\cancel{^{\circ}}}}\\&=&\frac{\pi}{6}rad\end{eqnarray}}\)
他にもみていくと、同様の計算を行って
\(\displaystyle{\begin{eqnarray}45^{\circ}&=&45×\frac{\pi}{180}\frac{rad\cdot\textcolor{blue}{\cancel{^{\circ}}}}{\textcolor{blue}{\cancel{^{\circ}}}}\\&=&\frac{\pi}{4}rad\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}60^{\circ}&=&60×\frac{\pi}{180}\frac{rad\cdot\textcolor{blue}{\cancel{^{\circ}}}}{\textcolor{blue}{\cancel{^{\circ}}}}\\&=&\frac{\pi}{3}rad\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}90^{\circ}&=&90×\frac{\pi}{180}\frac{rad\cdot\textcolor{blue}{\cancel{^{\circ}}}}{\textcolor{blue}{\cancel{^{\circ}}}}\\&=&\frac{\pi}{2}rad\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}120^{\circ}&=&120×\frac{\pi}{180}\frac{rad\cdot\textcolor{blue}{\cancel{^{\circ}}}}{\textcolor{blue}{\cancel{^{\circ}}}}\\&=&\frac{2}{3}{\pi}rad\end{eqnarray}}\)
このように、\(^{\circ}\)(度)とrad(ラジアン)を変換することができます。
これを実際に用いて\(\sin\theta、\cos \theta 、\tan \theta \)の値をみていきます。
例として、\(\theta=\frac{\pi}{6}\)のとき、
\(\pi{rad}=180^{\circ}\Leftrightarrow\pi=180^{\circ}/rad\)
から、
\(\displaystyle{\begin{eqnarray}\frac{\textcolor{red}{\pi}}{6}rad&=&\frac{1}{6}rad×\textcolor{red}{180\frac{^{\circ}}{rad}}\\&=&\frac{180}{6}\frac{^{\circ}\cdot\textcolor{blue}{\cancel{rad}}}{\textcolor{blue}{\cancel{rad}}}\\&=&30^{\circ}\end{eqnarray}}\)
なので、\(\theta=\frac{\pi}{6}rad=30^{\circ}\)となり、それぞれの三角関数の値は\(\theta=30^{\circ}\)の場合と同様となります。
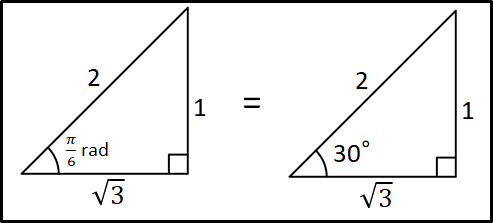
よって、
\(\sin{\frac{\pi}{6}}(=\sin{30^{\circ}})=\frac{1}{2}\)
\(\cos{\frac{\pi}{6}}(=\cos{30^{\circ}})=\frac {\sqrt{3}}{2}\)
\(\tan{\frac{\pi}{6}}(=\tan{30^{\circ}})=\frac {1}{\sqrt{3}}\)
となります。
2.単位円による三角関数の定義
2-1.\(\sin\theta\)と\(\cos\theta\)について
単位円とは半径が1の円のことです。
原点Oが円の中心である単位円を考え、この単位円上に点Pをとります。そして原点Oと点Pを結んだ直線をOPとすると下図のようになります。
点Pの\(x-y\)座標をそれぞれ\((x、y)\)とします。
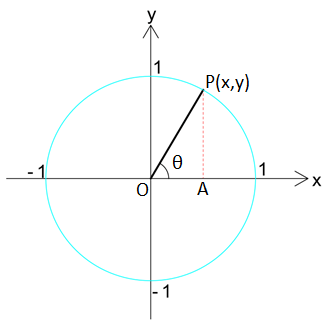
点Pから\(x\)軸に垂直に線を引き、その線と\(x\)軸との交点をAとすると直角三角形OPAができます。
この直角三角形OPAに注目してみると、点Pの座標が\((x、y)\)なので\(OA=x\)、\(AP=y\)となります。
ここで、\(\sin\theta\)と\(\cos\theta\)を考えてみると、
\(\displaystyle{\begin{eqnarray}\sin\theta&=&\frac{AP}{OP}=\frac{y}{1}\\{\Leftrightarrow}y&=&\sin\theta\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\cos\theta&=&\frac{OA}{OP}=\frac{x}{1}\\{\Leftrightarrow}x&=&\cos\theta\end{eqnarray}}\)
となります。
このことから、点Pの座標は\((\cos\theta,\sin\theta)\)で表されることが分かります。
このように、単位円上の点Pの\(x\)座標が\(\cos\theta\)、(y)座標が\(\sin\theta\)と三角関数を定義することができます。
また、OPとx軸のなす角\(\theta\)は半時計回り(左回り)を正、時計回り(右回り)を負とします。
\(\bf{\underline{1)[\theta=0rad]のとき}}\)
点Pは\(x\)軸上にあるので、\(y\)座標は0となります。
また\(x\)座標は単位円の半径1と等しくなるので、1となります。
\(y\)座標は\(\sin\theta\)と等しく、\(x\)座標は\(\cos\theta\)と等しいので、
\(\cos0=1\)
\(\sin0=0\)
となります。

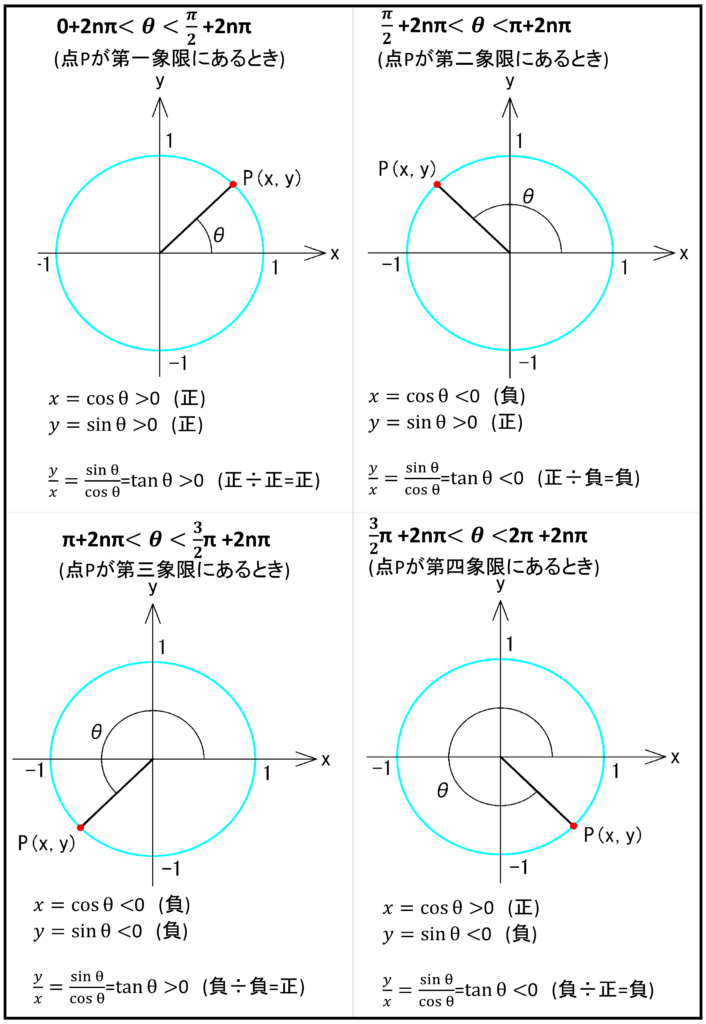
\(\bf{\underline{2)[0\lt\theta\lt\frac{\pi}{2}(=90^{\circ})]のとき}}\)
点Pは第1象限にあるので座標は\(x\gt0\)、\(y\gt0\)となります。
すなわち、\(x=\cos\theta\gt0\)、\(y=\sin\theta\gt0\)となります。

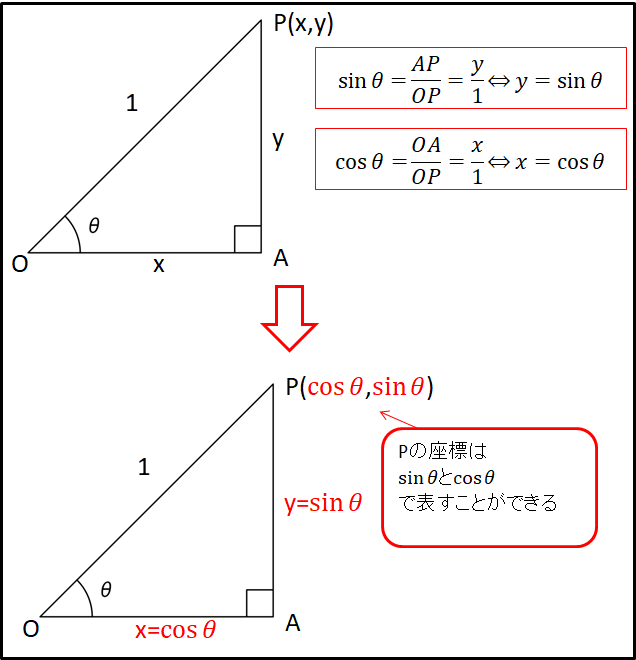
例)\(\theta=\frac{\pi}{4}rad(=45^{\circ})\)のとき
\(x=\sin{\frac{\pi}{4}}=\frac{1}{\sqrt{2}}\gt0\)
\(y=\cos{\frac{\pi}{4}}=\frac{1}{\sqrt{2}}\gt0\)
となります。
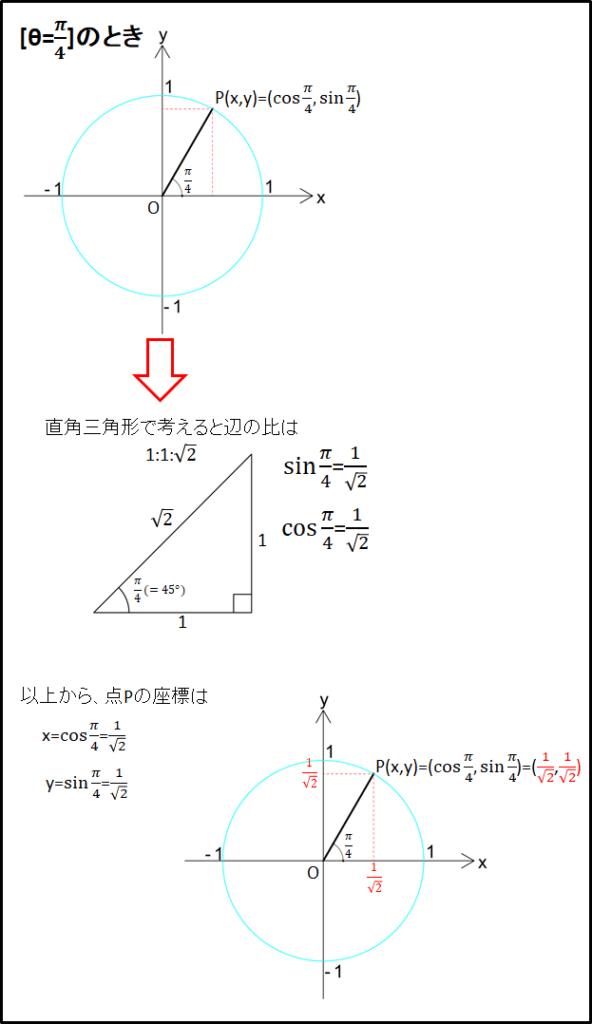
\(\bf{\underline{3)[\theta=\frac{\pi}{2}rad]のとき}}\)
点Pは\(y\)軸上にあり、単位円の半径1と等しくなるので\(y\)座標は1となります。
また点Pが\(y\)軸上にあるので、\(x\)座標は0となります。
\(y\)座標は\(\sin\theta\)と等しく、\(x\)座標は\(\cos\theta\)と等しいので、
\(\cos{\frac{\pi}{2}}=0\)
\(\sin{\frac{\pi}{2}}=1\)
となります。
\(\bf{\underline{4)[\frac{\pi}{2}\lt\theta\lt\pi(=180^{\circ})]のとき}}\)
点Pは第2象限にあるので座標は\(x\lt0\)、\(y\gt0\)となる。
すなわち、\(x=\cos\theta\lt0\)、\(y=\sin\theta\gt0\)となる。
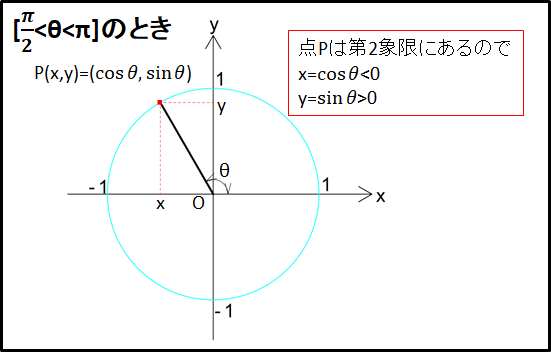
例)\(\theta=\frac{2}{3}{\pi}rad(=120^{\circ})\)のとき
下図状況を考えます。
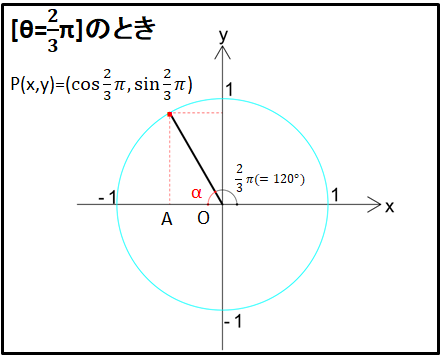
このとき三角形OPAの\(\textcolor{red}{\angle\alpha}\)は
\(\begin{eqnarray}\alpha&=&\pi-\frac{2}{3}\pi\\&=&\frac{\pi}{3}\end{eqnarray}\)
となります。
よって、三角形OPAに注目してみると、
\(\textcolor{red}{\angle\alpha}=\textcolor{red}{\frac{\pi}{3}}\)
なので、隣辺OAと対辺APの長さはそれぞれ
\(OA=\cos{\frac{\pi}{3}}=\frac{1}{2}\)
\(AP=\sin{\frac{\pi}{3}}=\frac{\sqrt{3}}{2}\)
となります。
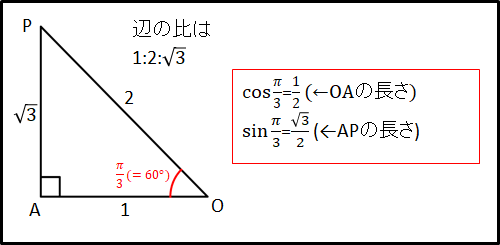
三角形OPAの隣辺と対辺の長さはわかりましたが、点Pは第2象限にあります。
よって、点Pの\(x\)座標は原点から\(x\)軸の負の方向(マイナスの方向)にOA\((=\frac{1}{2})\)だけ進んだところ、\(y\)座標は原点から\(y\)軸の正の方向(プラスの方向)にAP\((=\frac{\sqrt{3}}{2})\)だけ進んだところにあります。
以上から、\(\theta=\frac{2}{3}\pi\)のとき、\(\sin\theta\)と\(\cos\theta\)の値はそれぞれ、
\(\sin{\frac{2}{3}\pi}=\frac{\sqrt{3}}{2}\)
\(\cos{\frac{2}{3}\pi}=-\frac{1}{2}\)
となります。
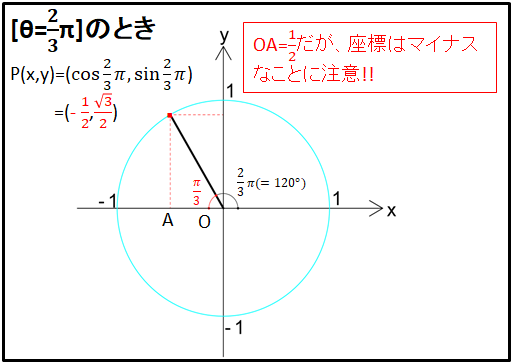
このように、\([\frac{\pi}{2}\lt\theta\lt\pi(=180^{\circ})]\)の範囲で考えるときは、直角三角形OPAのように角度\(\pi-\theta\)の直角三角形を考えるとわかりやすいと思います。
\(x,y\)の大きさ(絶対値)は角度\(\pi-\theta\)の直角三角形の辺の長さで考え、その符号は単位円上の点P\((\sin\theta,\cos\theta)\)がどこの象限にいるかで考えるといいと思います。
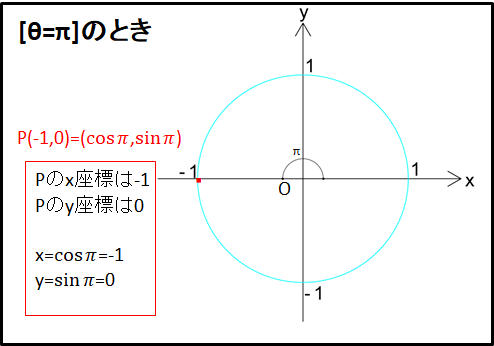
\(\bf{\underline{5)[\theta={\pi}rad]のとき}}\)
点Pは\(x\)軸上にあり、大きさは単位円の半径1と等しく符号はマイナスになるので\(x\)座標は-1となります。
また点Pが\(x\)軸上にあるので、\(y\)座標は0となります。
\(y\)座標は\(\sin\theta\)と等しく、\(x\)座標は\(\cos\theta\)と等しいので、
\(\cos{\pi}=-1\)
\(\sin{\pi}=0\)
となります。
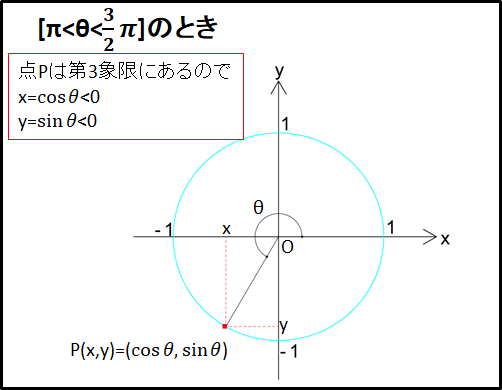
\(\bf{\underline{6)[\pi\lt\theta\lt\frac{3}{2}\pi(=270^{\circ})]のとき}}\)
点Pは第3象限にあるので座標は\(x\lt0\)、\(y\lt0\)となります。
すなわち、\(x=\cos\theta\lt0\)、\(y=\sin\theta\lt0\)となります。
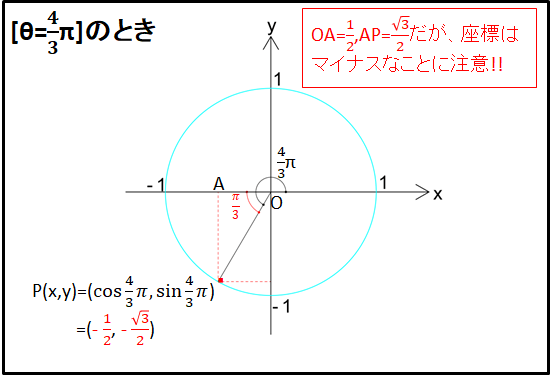
例)\(\theta=\frac{4}{3}{\pi}rad(=240^{\circ})\)のとき
\(\theta=\frac{2}{3}{\pi}rad(=120^{\circ})\)のときと同様に、座標の絶対値は直角三角形で考えて符号は図で考えます。
下図三角形OPAとその角度\(\alpha\)に注目すると、\(\alpha=\frac{4}{3}\pi-\pi=\frac{\pi}{3}(=60^{\circ})\)となります。
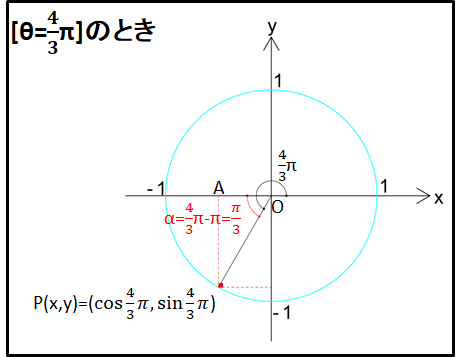
これから、隣辺OAと対辺APの長さはそれぞれ
\(OA=\cos{\frac{\pi}{3}}=\frac{1}{2}\)
\(AP=\sin{\frac{\pi}{3}}=\frac{\sqrt{3}}{2}\)
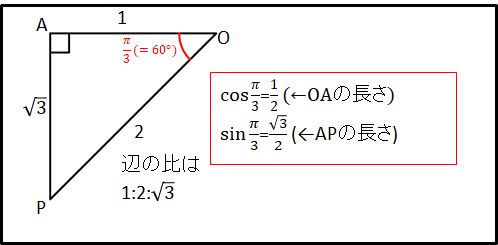
符号を考えると、\(x\lt0\),\(y\lt0\)なので、
\(\cos{\frac{4}{3}\pi}=-\frac{1}{2}\)
\(\sin{\frac{4}{3}\pi}=-\frac{\sqrt{3}}{2}\)
となります。
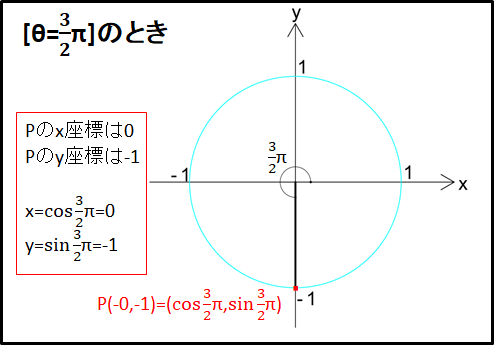
\(\bf{\underline{7)[\theta=\frac{3}{2}\pi(=270^{\circ})]のとき}}\)
点Pは\(y\)軸上にあるので\(x\)座標は0となります。
また\(y\)座標の位置は、大きさは単位円の半径1と等しく符号はマイナスになるので\(y\)座標は-1となります。
\(y\)座標は\(\sin\theta\)と等しく、\(x\)座標は\(\cos\theta\)と等しいので、
\(\cos{\frac{3}{2}\pi}=0\)
\(\sin{\frac{3}{2}\pi}=-1\)
となります。
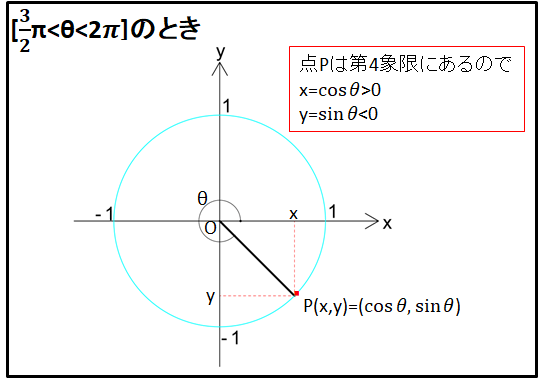
\(\bf{\underline{8)[\frac{3}{2}\pi\lt\theta\lt2\pi(=360^{\circ})]のとき}}\)
点Pは第4象限にあるので座標は\(x\gt0\)、\(y\lt0\)となります。
すなわち、\(x=\cos\theta\gt0\)、\(y=\sin\theta\lt0\)となります。
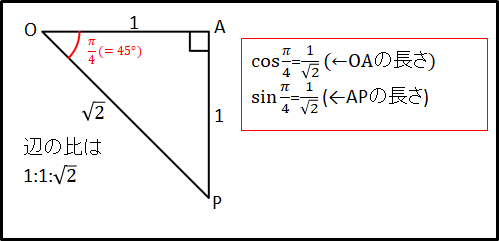
例)\(\theta=\frac{7}{4}{\pi}rad(=315^{\circ})\)のとき
これまでと同様に、座標の絶対値は直角三角形で考えて符号は図で考えます。
下図三角形OPAとその角度\(\alpha\)に注目すると、\(\alpha=2\pi-\frac{7}{4}\pi=\frac{\pi}{4}(=45^{\circ})\)となります。
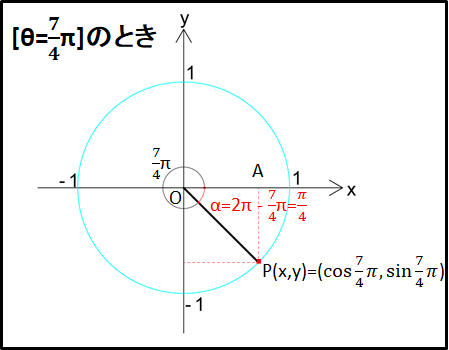
このことから、隣辺OAと対辺APの長さはそれぞれ
\(OA=\cos{\frac{\pi}{4}}=\frac{1}{\sqrt{2}}\)
\(AP=\sin{\frac{\pi}{4}}=\frac{1}{\sqrt{2}}\)
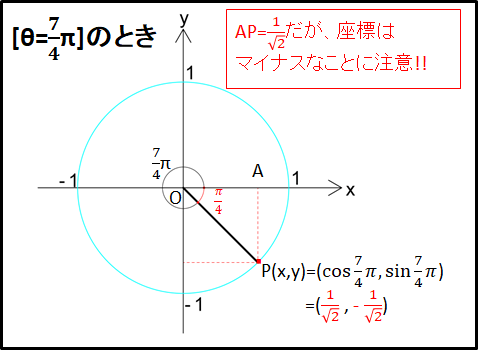
符号を考えると、\(x\gt0\),\(y\lt0\)なので、
\(\cos{\frac{\pi}{4}}=\frac{1}{\sqrt{2}}\)
\(\sin{\frac{\pi}{4}}=-\frac{1}{\sqrt{2}}\)
となります。
\(\bf{\underline{9)[\theta=2\pi(=360^{\circ})]のとき}}\)
点Pの位置は、\(\theta=0\)のときと同じなので、
\(\cos{2\pi}=1\)
\(\sin{2\pi}=0\)
となります。
2-2.\(\sin\theta\)と\(\cos\theta\)の周期
\(\theta\gt2\pi\)のときを考えてみます。
点Pが単位円上を動くとき、\(\theta=2\pi(=360^{\circ})\)動くと元の位置に戻ります。
その後、同じように円周を動きます。
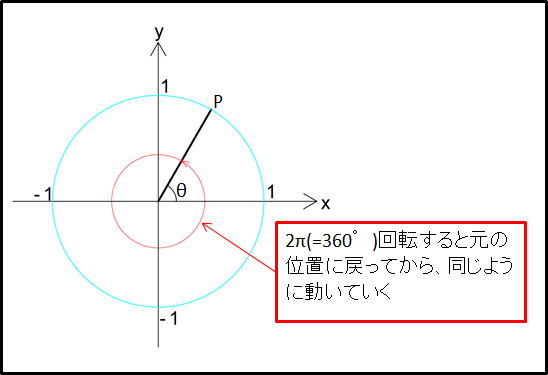
上図から、角度\(\theta\)の位置から\(2\pi(=360^{\circ})\)回転すると元の\(\theta\)の位置に戻るので、\(\sin{\theta}\)と\(\cos{\theta}\)の値は\(2\pi\)回転する前と後で同じ値となります。
このことから、
\(\sin{(\theta+2\pi)}=\sin{\theta}\)
\(\cos{(\theta+2\pi)}=\cos{\theta}\)
が成り立ちます。
同様にして、点Pは\(2\pi,4\pi,6\pi\cdots\)と、\(2\pi(=360^{\circ})\)の整数倍ごとに元の位置に戻るので、一般に整数\(n(\cdots,-2,-1,0,1,2,\cdots)\)を用いて
\(\sin{(\theta+2n\pi)}=\sin{\theta}\)
\(\cos{(\theta+2n\pi)}=\cos{\theta}\)
が成り立ちます。
\(\sin{\theta}\)および\(\cos{\theta}\)は\(2\pi\)ごとに同じ形を繰り返すので、このことを\(\textcolor{red}{\underline{\sin\theta,\cos\thetaは2\piの周期をもつ}}\) といいます。
三角関数の式からは、\(2\pi\theta\)の分母が周期となります。

2-3.\(\tan\theta\)について
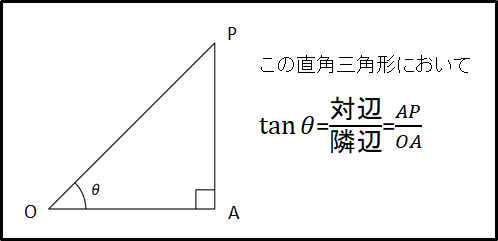
下図直角三角形OPAにおいて、\(\tan\theta\)はさきにみたように
\(\tan\theta=\frac{AP}{OA}\)
となります。
これを単位円で考えていきます。
単位円においても、円周上の点Pと、そこから\(x\)軸に垂直に下ろした線と\(x\)軸との交点をAとした直角三角形OAPを考えます。
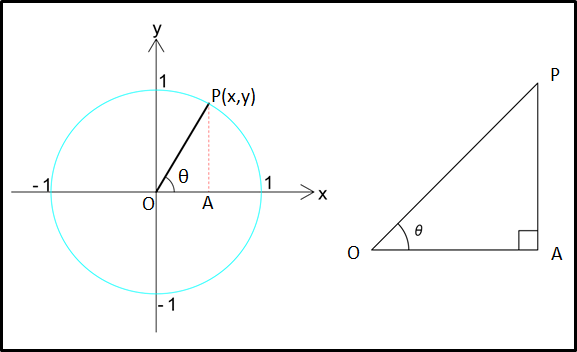
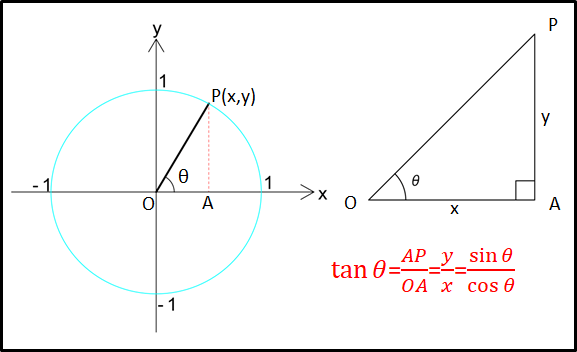
この直角三角形において、
\(\tan\theta=\frac{AP}{OA}\)
また、\(OA=x=\cos\theta,AP=y=\sin\theta\)なので
\(\displaystyle{\begin{eqnarray}\tan\theta&=&\frac{AP}{OA}\\&=&\frac{y}{x}\\&=&\frac{\sin\theta}{cos\theta}\end{eqnarray}}\)
となります。
\(\tan\theta\)は\(\sin\theta\)と\(\cos\theta\)で表されるので、符号は\(\theta\)の範囲による\(x(=\cos\theta),y(=\sin\theta)\)の符号で決まります。
例)\(\theta=\frac{2}{3}{\pi}rad(=120^{\circ})\)のとき
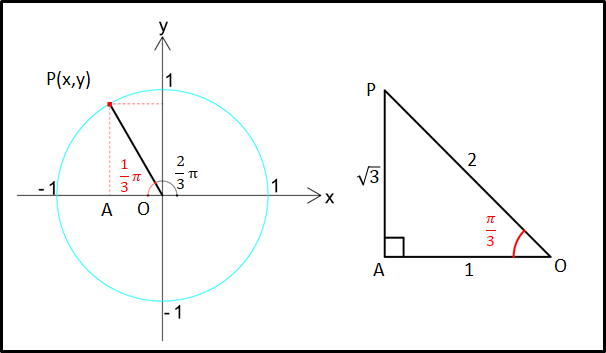
\(\theta=\frac{1}{3}\pi\)の直角三角形と点Pの位置を考えます。
\(x,y\)の大きさはそれぞれ\(\cos{\frac{1}{3}\pi}=\frac{1}{2},\sin{\frac{1}{3}\pi}=\frac{\sqrt{3}}{2}\)であり、点Pの位置を考えると\(x\lt0,y\gt0\)なので、
\(x=\cos{\frac{2}{3}\pi}=-\frac{1}{2}\)
\(y=\sin{\frac{2}{3}\pi}=\frac{\sqrt{3}}{2}\)
となります。
以上から、\(\tan{{\frac{2}{3}\pi}}\)は、
\(\displaystyle{\begin{eqnarray}\tan{\frac{2}{3}\pi}&=&\frac{y}{x}\\&=&\frac{\sin{\frac{2}{3}\pi}}{\cos{\frac{2}{3}\pi}}\\&=&\frac{\frac{\sqrt{3}}{2}}{-\frac{1}{2}}\\&=&-\frac{\sqrt{3}}{2}×2\\&=&-\sqrt{3}\end{eqnarray}}\)
となります。
\(\tan\theta\)は\(\tan\theta=\frac{y}{x}\)から、\(x=0\)、すなわち\(x=\cos\theta=0\)となる\(\theta=\frac{\pi}{2},\frac{3}{2}\pi,\frac{5}{2}\pi,\cdots\)では定義されません。(0で割ることはできない)
また\(\tan\theta=\frac{y}{x}\)の形から、\(\tan\theta\)は線分OPの傾きを表していることもわかると思います。
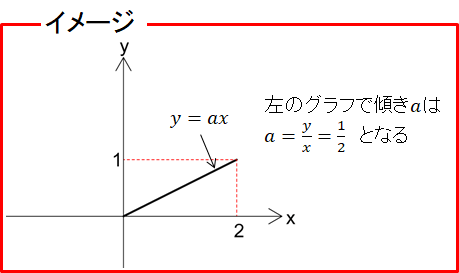
2-4.\(\tan\theta\)の周期
\(\tan\theta\)は傾きに等しいので、\(x=1\)上の点の\(y\)座標に等しいともいえます。
(原点を通る直線\(y=ax\)を考えると、傾き\(a=\tan\theta\)なので、\(y=\tan{\theta}x\)となる。\(x=1\)のとき、\(y=\tan\theta\)となる)
\(\tan\theta\)は、\(\theta=\frac{\pi}{2},\frac{3}{2}\pi,\frac{5}{2}\pi,\cdots\)では定義されないので
\([-\frac{\pi}{2}\lt\theta\lt\frac{\pi}{2}]\)の範囲で\(\tan\theta\)は\(x=1\)上を\(-\infty\)から\(\infty\)まで動きます。
(\(\theta\)は半時計回り(左回り)を正、時計回り(右回り)を負)
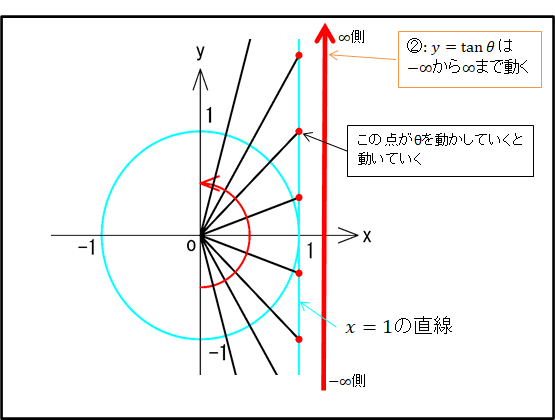
同様に考えて、\([\frac{\pi}{2}\lt\theta\lt\frac{3\pi}{2}]\)の範囲では、\(\tan\theta\)は\(x=1\)上を\(-\infty)から(\infty\)まで動きます。
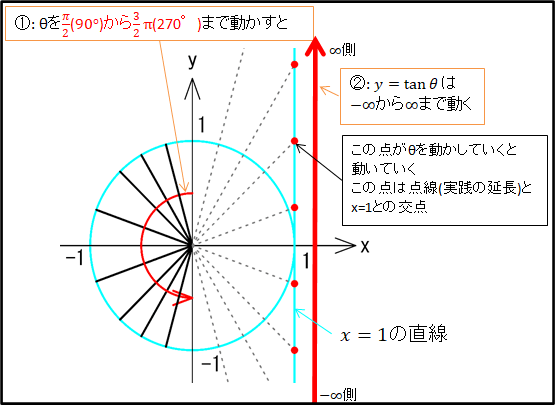
以上から\(\tan\theta\)は、\((-\frac{\pi}{2}\lt\theta\lt\frac{\pi}{2}),(\frac{\pi}{2}\lt\theta\lt\frac{3}{2}\pi),(\frac{3}{2}\pi\lt\theta\lt\frac{5}{2}\pi),\cdots\)
というように、\(\pi\)ごとに同じ形を繰り返し、\(\tan(\theta+\pi)=\tan\theta\)となります。
一般に整数\(n\)を用いて、\(\tan(\theta+n\pi)=\tan\theta\)が成り立ち、\(\textcolor{red}{周期は\pi}\)となります。
三角関数の式からは、\(\pi\theta\)の分母が周期となります。
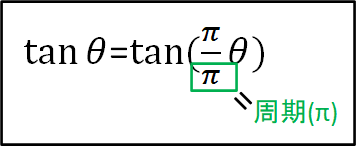
2-5.象限と符合のまとめ
ここで、それぞれの単位円上の位置における三角関数の符合についてまとめておきます。
また、有名角における三角関数の値も載せておきます。
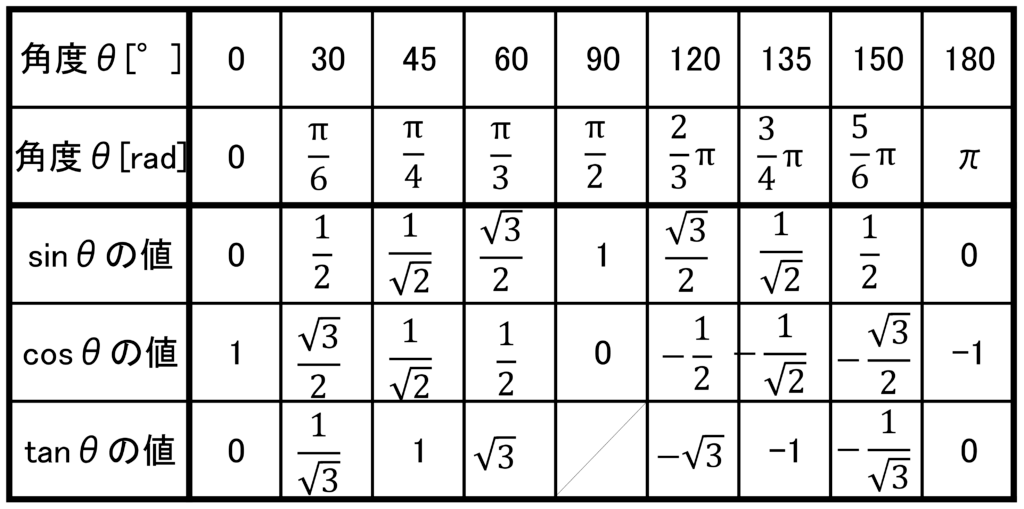
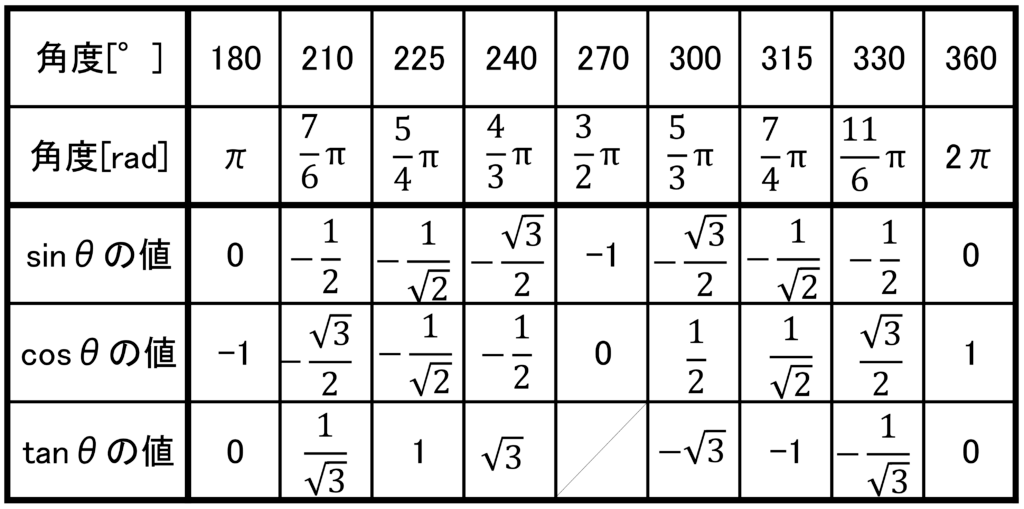
3.三角関数の関係式
次に、下記の3つの基本的な三角関数の関係式について説明していきます。
\(\displaystyle{\begin{eqnarray}\tan\theta=\frac{\sin\theta}{\cos\theta}\cdots(1)&&\\{\sin}^2\theta+{\cos}^2\theta=1\cdots(2)&&\\1+{\tan}^2\theta=\frac{1}{{\cos}^2\theta}\cdots(3)\end{eqnarray}}\)
\((1)\)については、\(\tan\theta\)の定義によるものになります。
\((2)\)については、単位円での定義において、
\(x=\cos\theta ,y=\sin\theta\)
また、この\(x,y\)は単位円(半径が1の円)上にあるので、円の方程式\(x^2+y^2=1\)に\(x=\cos\theta ,y=\sin\theta\)をそれぞれ代入して、
\(\displaystyle{\begin{eqnarray}&&{(\cos\theta)}^2+{(\sin\theta)}^2=1\\\Leftrightarrow&&{\sin}^2\theta+{\cos}^2\theta=1\end{eqnarray}}\)
となります。
\((3)\)について
\((2)\)の式を両辺\(\cos^2\theta\)で割って、
\(\displaystyle{\begin{eqnarray}&&\frac{\sin^2\theta}{\cos^2\theta}+\frac{\cos^2\theta}{\cos^2\theta}=\frac{1}{\cos^2\theta}\\\Leftrightarrow&&\left(\frac{\sin\theta}{\cos\theta}\right)^2+1=\frac{1}{\cos^2\theta}\\\Leftrightarrow&&1+\tan^2\theta=\frac{1}{\cos^2\theta}\end{eqnarray}}\)
今回は以上になります。
次回は、三角関数のグラフについて説明します。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


