投稿日:
【高校物理】三角関数練習問題1:定義とグラフ【高校数学】【三角関数】【練習問題】
\(\require{color}\)
\(\require{cancel}\)
こちらは、”2-1.三角関数の定義と関係式”と”2-2.三角関数のグラフ”における内容の練習問題となります。
なるべく、物理で用いるような内容にしましたので、解いてみてください。
三角関数に関する記事は、こちらも参考にしてください。
→三角関数の定義と関係式
→三角関数のグラフ
→三角関数の公式
→練習問題2(三角方程式と公式)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1-1.単位ラジアンと三角関数の値/問題
\(\mathbf{[問題1-1]}\)
\(\theta=0^{\circ} ,30^{\circ} ,45^{\circ} ,60^{\circ} ,90^{\circ}\)をそれぞれ単位をラジアン[rad]に直し、各\(\theta\)における\(\sin\theta\) ,\(\cos\theta\) ,\(\tan\theta\)の値をそれぞれ求めよ。
1-2.単位ラジアンと三角関数の値/解答
\(\mathbf{[問題1-1]の解答}\)
単位[\(^{\circ}\)]と[rad]の関係は、
\(\displaystyle{180^{\circ}={\pi}rad}\)
なので、両辺\(180^{\circ}\)で割って、
\(\displaystyle{\begin{eqnarray}&&180^{\circ}={\pi}rad\\\\\Leftrightarrow&&1=\frac{\pi}{180}rad/^{\circ}\end{eqnarray}}\)
これを用いて、角度\(x^{\circ}\)の単位を[rad]に直すには、
\(\displaystyle{\begin{eqnarray}x^{\circ}×\frac{\pi}{180^{\circ}}rad/^{\circ}&=&x×\frac{\pi}{180}\frac{rad・^{\textcolor{blue}{\circ}}}{^{\textcolor{blue}{\circ}}}\\\\&=&x×\frac{\pi}{180}\frac{rad・^{\textcolor{blue}{\cancel{\circ}}}}{^{\textcolor{blue}{\cancel{\circ}}}}\\\\&=&x×\frac{\pi}{180}rad\end{eqnarray}}\)
よって、単位が[\(^{\circ}\)]であるものに\(\frac{\pi}{180}\)を掛ければ、[rad]単位に直すことができます。
単位についてはこちらも参考にしてください
→単位の計算と換算方法
以上から、
\(\displaystyle{0^{\circ}×\frac{\pi}{180}\frac{rad}{^{\circ}}=0rad}\)
\(\displaystyle{30^{\circ}×\frac{\pi}{180}\frac{rad}{^{\circ}}=\frac{\pi}{6}rad}\)
\(\displaystyle{45^{\circ}×\frac{\pi}{180}\frac{rad}{^{\circ}}=\frac{\pi}{4}rad}\)
\(\displaystyle{60^{\circ}×\frac{\pi}{180}\frac{rad}{^{\circ}}=\frac{\pi}{3}rad}\)
\(\displaystyle{90^{\circ}×\frac{\pi}{180}\frac{rad}{^{\circ}}=\frac{\pi}{2}rad}\)
となります。
また、それぞれの三角関数の値は有名角の直角三角形の辺の比と単位円での定義から求めます。
有名角の辺の比は下のようになります。
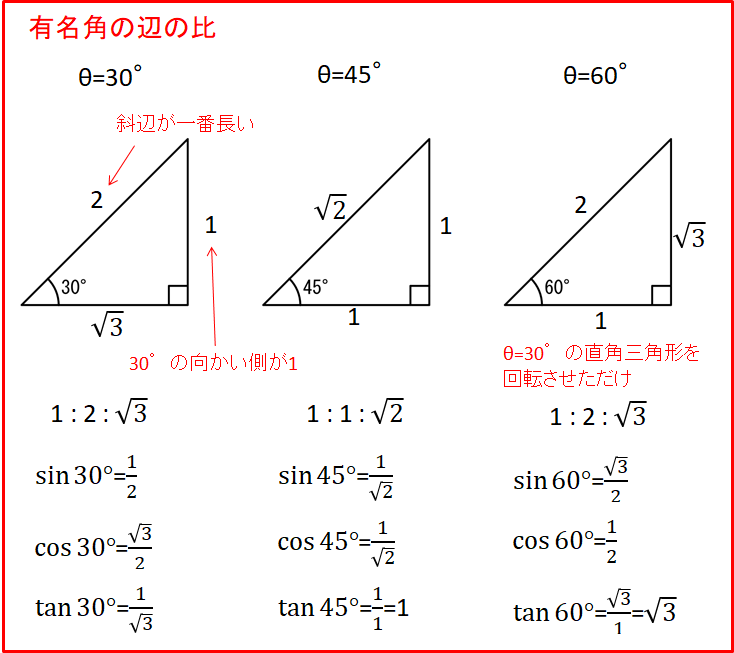
また単位円での定義では、単位円上の点Pの\(y\)座標が\(\sin\theta\)の値、\(x\)座標が\(\cos\theta\)の値となります。
よって、
\(\underline{\bf{\theta=0のとき}}\)
\(\sin0=0\)
\(\cos0=1\)

\(\tan\theta\)の値は、定義から\(\tan\theta=\frac{\sin\theta}{\cos\theta}\)なので、
\(\displaystyle{\begin{eqnarray}\tan0&=&\frac{\sin0}{\cos0}\\\\&=&\frac{0}{1}\\\\&=&0\end{eqnarray}}\)
となります。
\(\underline{\bf{\theta=\frac{\pi}{2}のとき}}\)
\(\theta=0\)の時と同様、単位円での定義から、
\(\sin\frac{\pi}{2}=1\)
\(\cos\frac{\pi}{2}=0\)
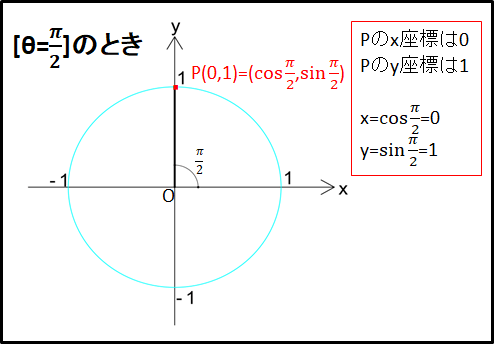
また、\(\tan\frac{\pi}{2}\)は定義から分母の\(\cos\frac{\pi}{2}\)の値が\(0\)となってしまい、分母に\(0\)はとれないので\(\tan\frac{\pi}{2}\)の値は定義されません。
(\(\tan\theta\)は単位円の中心Oと単位円上の点Pを結んだ直線の傾きを表します。\(\theta\)が\(\frac{\pi}{2}\)に近づくと、傾きはとても大きくなっていくので\(\tan\theta\)は\(+\infty\)に近づいていきます。)
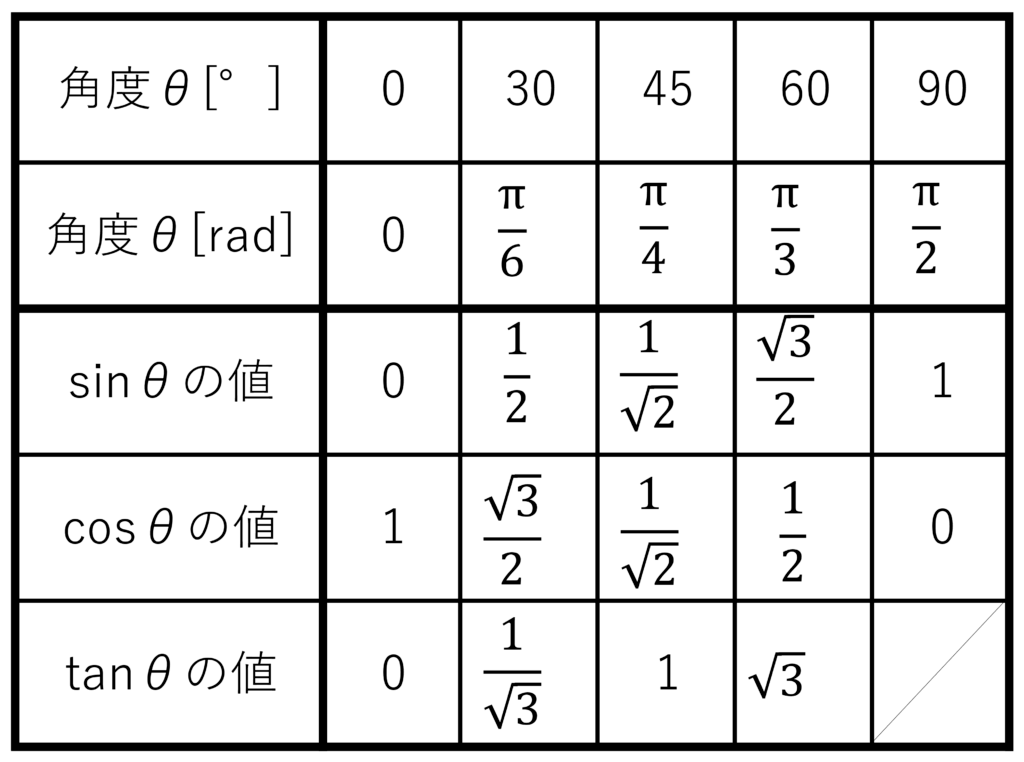
解答を表にまとめておきます。
2-1.辺の長さの計算/問題
\(\mathbf{[問題2-1]}\)
次の直角三角形①、②に関して、OPAのOA,PAの辺の長さを求めよ(②は\(r\),\(\theta\)を用いて)
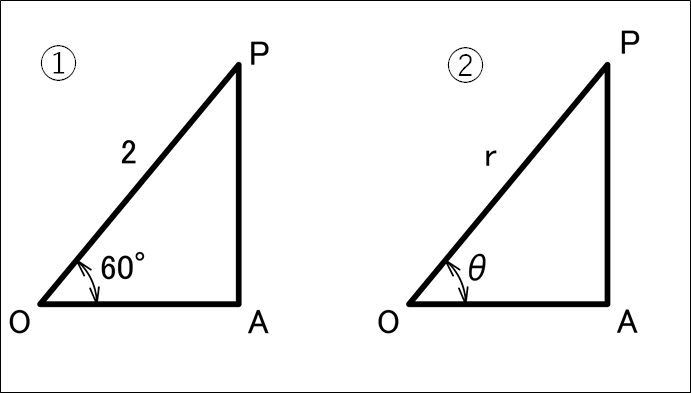
2-2.辺の長さの計算/解答
\(\mathbf{[問題2-1]の解答}\)
三角関数の定義から、
\(\displaystyle{\begin{eqnarray}&&\cos\theta=\frac{OA}{OP}\\\\\Leftrightarrow&&{OA}=\textcolor{red}{OP\cos\theta}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}&&\sin\theta=\frac{PA}{OP}\\\\\Leftrightarrow&&{PA}=\textcolor{red}{OP\sin\theta}\end{eqnarray}}\)
以上から、
\(\underline{\bf{①の解答}}\)
\(\cos60^{\circ}=\frac{1}{2}\)
\(\sin60^{\circ}=\frac{\sqrt{3}}{2}\)
なので、
\(\displaystyle{\begin{eqnarray}OA&=&OP×\cos60^{\circ}\\\\&=&2×\frac{1}{2}\\\\&=&1\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}PA&=&OP×\sin60^{\circ}\\\\&=&2×\frac{\sqrt{3}}{2}\\\\&=&\sqrt{3}\end{eqnarray}}\)
\(\underline{\bf{②の解答}}\)
\(\displaystyle{\begin{eqnarray}OA&=&OP×\cos\theta\\&=&r×\cos\theta\\&=&r\cos\theta\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}PA&=&OP×\sin\theta\\&=&r×\sin\theta\\&=&r\sin\theta\end{eqnarray}}\)
解答は以上になります。
斜辺と角度\(\theta\)から他の辺を求めるには、今回のように定義から式変形をしてもよいですが、
\(\displaystyle{\bf{\textcolor{red}{(\thetaの向かい側の辺)=”斜辺×\sin\theta”}}}\)
\(\displaystyle{\bf{\textcolor{red}{(\thetaにへばりついている辺)=”斜辺×\cos\theta”}}}\)
は覚えておくとよいと思います。
計算が多少は早くなりますし、物理では多用します。
3-1.三角関数のグラフ/問題
\(\mathbf{[問題3-1]}\)
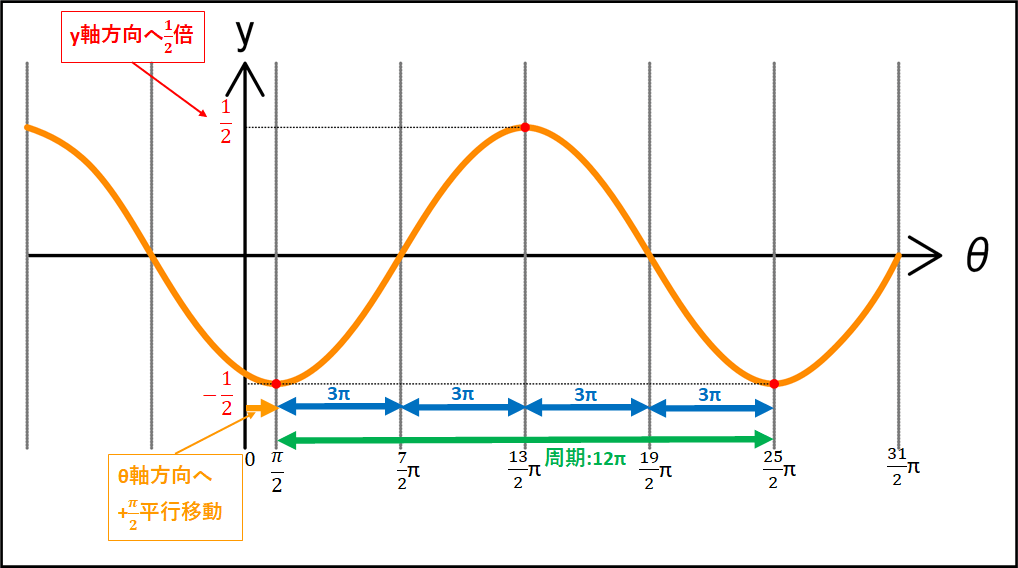
\(\displaystyle{y=-\frac{1}{2}\cos(\frac{\theta}{6}-\frac{\pi}{12}})\)のグラフを描け。
3-2.三角関数のグラフ/解答
\(\mathbf{[問題3-1]の解答}\)
まず以下のことを確認します。
\(\textcolor{red}{①y軸または\theta軸方向への平行移動}\)
\(\textcolor{red}{②y軸方向への拡大・縮小}\)
\(\textcolor{red}{③\theta軸方向への拡大・縮小}\)
問題文の式を変形して、
\(\displaystyle{\begin{eqnarray}y&=&-\frac{1}{2}\cos(\frac{\theta}{6}-\frac{\pi}{12})\\\\&=&-\frac{1}{2}\cos\frac{1}{6}(\theta-\frac{\pi}{2})\\\\&=&\textcolor{red}{-\frac{1}{2}}\cos\frac{2\pi}{\textcolor{green}{12\pi}}(\theta-\textcolor{#ffd700}{\frac{\pi}{2}})\end{eqnarray}}\)
以上から問題の式は、\(y=-\cos\theta\)のグラフを
①\(\theta\)軸方向へ\(+\textcolor{#ffd700}{\frac{\pi}{2}}\)平行移動
②\(y\)軸方向へ\(\textcolor{red}{\frac{1}{2}}\)縮小
③\(\theta\)軸方向へ6倍へ拡大
したものであることが分かります。
※\(-\cos\theta\)型のグラフは、\(y=\cos\theta\)のグラフを\(\theta\)軸に関して対称にしたもの
※周期は\(2\pi\theta\)の分母なので、\(12\pi\)となる。これは\(y=\cos\theta\)の周期\(2\pi\)を\(6\)倍したもの
これをふまえてグラフの概形を描きます。(縮尺は適当です)
今回の練習問題は以上になります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


