投稿日:
【高校物理】積分法の応用【高校数学】【積分】
\(\require{color}\)
\(\require{cancel}\)
こちらは、積分法の応用となっています。
主に、微分法とその応用で扱った内容から、積分を求めています。
置換積分や部分積分、また区分求積法について解説しています。
また、積分と面積や体積の関係も扱っています。
微分・積分に関する記事は、こちらも参考にしてください
→微分係数と導関数
→積分法
→様々な関数
→極限
→微分法とその応用
→よく使う積分の考え方と微積公式まとめ
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.不定積分
1-1.不定積分復習
「積分法」の復習となりますが、\(F'(x)=f(x)\)のとき、\(f(x)\)の不定積分は
\(\displaystyle{\int{f(x)}dx=F(x)+C}\)
となります。
\(f(x)\)の不定積分を求めることを積分するといい、\(C\)を積分定数といいます。
また、\(f(x)\)を被積分関数(積分される関数という意味)、\(x\)を積分変数といいます。
\(\underline{x^{\alpha}{\bf{の不定積分}}}\)
実数\(\alpha\)について、「微分法とその応用」で扱ったように、
\(\displaystyle{(x^{\alpha+1})’=({\alpha+1})x^{\alpha}}\)
が成り立ちます。
また、
\(\displaystyle{(\log|x|)’=\frac{1}{x}}\)
が成り立つので、次のことがいえます。
\(\displaystyle{\int{x^{\alpha}}dx=\frac{1}{\alpha+1}x^{\alpha+1}+C (\alpha\neq-1)}\)
\(\displaystyle{\int\frac{1}{x}dx=\log|x|+C}\)
\(\underline{\bf{定数倍/和・積の不定積分}}\)
定数倍・和・積に関する不定積分は以下のようなものでした。
\(\displaystyle{\int{kf(x)}dx=k\int{f(x)}dx}\)
\(\displaystyle{\int\left\{f(x)+g(x)\right\}dx=\int{f(x)}dx+\int{g(x)}dx}\)
\(\displaystyle{\int\left\{f(x)-g(x)\right\}dx=\int{f(x)}dx-\int{g(x)}dx}\)
1-2.様々な不定積分
「微分法とその応用」で扱った微分から、三角関数・指数関数の不定積分を求めることができます。
\(\underline{\bf{三角関数の不定積分}}\)
三角関数の微分はそれぞれ
\(\displaystyle{(\sin{x})’=\cos{x}}\)
\(\displaystyle{(\cos{x})’=-\sin{x}}\)
\(\displaystyle{(\tan{x})’=\frac{1}{\cos^2{x}}}\)
でした。
積分は微分の逆の計算をすることといえるので、三角関数の不定積分について次のことがいえます。
\(\displaystyle{\textcolor{red}{\int{\sin{x}}dx=-\cos{x}+C}}\)
\(\displaystyle{\textcolor{red}{\int{\cos{x}}dx=\sin{x}+C}}\)
\(\displaystyle{\textcolor{red}{\int{\frac{1}{\cos^2{x}}}dx=\tan{x}+C}}\)
\(\underline{\bf{指数関数の不定積分}}\)
指数関数の微分は以下のようなものでした。
\(\displaystyle{(e^x)’=e^x}\)
\(\displaystyle{(a^x)’=a^x\log{a}}\)
以上のことから、指数関数の不定積分は以下のようになります。
\(\displaystyle{\textcolor{red}{\int{e^x}dx=e^x+C}}\)
\(\displaystyle{\textcolor{red}{\int{a^x}dx=\frac{a^x}{\log{a}}+C}}\)
1-3.置換積分
\(\underline{{f(ax+b)}{\bf{の不定積分}}}\)
関数\(f(x)\)の原始関数\(F(x)\)を用いて、合成関数\(f(ax+b)\)の不定積分を求めることを考えます。
\(F'(x)=f(x)\)なので、合成関数の微分法から
\(\displaystyle{\begin{eqnarray}\frac{d}{dx}F(ax+b)&=&aF'(ax+b)\\&=&af(ax+b)\end{eqnarray}}\)
から、次のことがいえます。
\(F'(x)=f(x)\)、\(a\neq0\)のとき
\(\displaystyle{\textcolor{red}{\int{f(ax+b)}dx=\frac{1}{a}F(ax+b)+C}}\)
※合成関数の微分法について、
\(ax+b=u\)とおくと、\(F(ax+b)=F(u)\)
また、
\(\displaystyle{\begin{eqnarray}\frac{du}{dx}&=&\frac{d}{dx}(ax+b)\\\\&=&a\end{eqnarray}}\)
したがって、
\(\displaystyle{\begin{eqnarray}\frac{d}{dx}F(ax+b)&=&\frac{d}{du}F(u)・\frac{du}{dx}\\\\&=&F'(u)・a\\\\&=&f(u)・a\\\\&=&af(ax+b)\end{eqnarray}}\)
となります。
計算例)
1) \(\sqrt{4x+1}\)の不定積分
\(\displaystyle{f(x)=\sqrt{x}=x^{\frac{1}{2}}}\)とすると、
\(\displaystyle{\int{x^{\alpha}}dx=\frac{1}{\alpha+1}x^{\alpha+1}+C}\)
から、
\(\displaystyle{\begin{eqnarray}\int{f(x)}dx&=&\int{x^{\frac{1}{2}}}dx\\\\&=&\frac{1}{\frac{1}{2}+1}x^{\frac{1}{2}+1}\\\\&=&\frac{1}{\frac{3}{2}}x^{\frac{3}{2}}\\\\&=&\frac{2}{3}x^{\frac{3}{2}}\end{eqnarray}}\)
また、\(f(x)=\sqrt{x}\)から\(f(4x+1)=\sqrt{4x+1}\)なので公式中の\(a\)は\(a=4\)
以上から、\(\displaystyle{\int{f(ax+b)}dx=\frac{1}{a}F(ax+b)+C}\)を用いて
\(\displaystyle{\begin{eqnarray}\int{\sqrt{4x+1}}dx&=&\int{(4x+1)^{\frac{1}{2}}}dx\\\\&=&\frac{1}{4}・\frac{1}{\frac{1}{2}+1}・(4x+1)^{\frac{1}{2}+1}+C\\\\&=&\frac{1}{4}・\frac{1}{\frac{3}{2}}・(4x+1)^{\frac{3}{2}}+C\\\\&=&\frac{1}{4}・\frac{2}{3}(4x+1)^1(4x+1)^{\frac{1}{2}}+C\\\\&=&\frac{1}{6}(4x+1)(\sqrt{4x+1})+C\end{eqnarray}}\)
となります。
2) \(\sin{3x}\)の不定積分
\(\displaystyle{f(x)=\sin{x}}\)とすると、
\(\displaystyle{\begin{eqnarray}\int{f(x)}dx&=&\int{\sin{x}}dx\\\\&=&-\cos{x}+C\end{eqnarray}}\)
また、\(f(x)=\sin{x}\)から\(f(3x)=\sin(3x)\)なので公式中の\(a\)は\(a=3\)
以上から、\(\displaystyle{\int{f(ax+b)}dx=\frac{1}{a}F(ax+b)+C}\)を用いて
\(\displaystyle{\begin{eqnarray}\int{\sin{3x}}dx=-\frac{1}{3}\cos(3x)+C\end{eqnarray}}\)
となります。
以上が\(f(ax+b)\)の不定積分の公式を用いた解法になりますが、次に解説する置換積分法を用いた方が分かりやすいと思うので、個人的には覚える必要は無いと思います。
\(\underline{\bf{置換積分法}}\)
\(F(x)\)を\(f(x)\)の原始関数とします。また、\(x\)が\(t\)の関数として\(x=g(t)\)と表されるとき、\(y=f(x)\)は\(t\)の関数でもあります。
(\(y=F(g(t))\)となり、\(t\)の関数となる)
\(g(t)\)が微分可能なとき
\(\displaystyle{\frac{dy}{dx}=F'(x)=f(x)}\)
\(\displaystyle{\frac{dx}{dt}=g'(t)}\)
となるので、
\(\displaystyle{\begin{eqnarray}\frac{dy}{dt}&=&\frac{dy}{dx}・\frac{dx}{dt}\\\\&=&f(x)g'(t)\\\\&=&f(g(t))・g'(t)\end{eqnarray}}\)
これより、\(y\)を2通りの不定積分で表すと次の置換積分の公式が成り立ちます。
\(\displaystyle{\textcolor{red}{\int{f(x)}dx=\int{f(g(t))g'(t)}dt (x=g(t))}}\)
※\(f(g(t))\)において、\(x=g(t)\)とする。
\(\int{f(x)}dx\)を考えると
\(\displaystyle{\frac{dx}{dt}=g'(t)}\)から、形式的に両辺に\(dt\)を掛けて
\(\textcolor{green}{dx=g'(t)dt}\)となる。
以上から、\(\int{f(x)}dx\)を積分変数\(t\)を用いて表すと
\(\int{f(x)}\textcolor{green}{dx}=\int{f(g(t))・\textcolor{green}{g'(t)dt}}\)
となる。
上記解説や公式を見ただけでは分かりにくいと思いますが、実際にどのように用いるかは計算例を見ていただけると理解しやすいかと思います。
計算例のうち2問は、\(f(ax+b)\)の導関数で扱った問題と同様の問題を用いています。
今回説明した置換積分による解法のほうが、扱いやすいと思っていただけると幸いです。
計算例)
1) \(\sqrt{4x+1}\)の不定積分
\(\int{\sqrt{4x+1}}dx\)において、\(t=4x+1\)とすると、
\(\sqrt{4x+1}=\sqrt{t}\)
また、
\(\displaystyle{\begin{eqnarray}&&t=4x+1\\\\\Leftrightarrow&&4x=t-1\\\\\Leftrightarrow&&x=\frac{1}{4}t-\frac{1}{4}\end{eqnarray}}\)
より、
\(\displaystyle{\frac{dx}{dt}=\frac{1}{4}}\)
ここで、形式的に上式の両辺に\(dt\)を掛けて
\(\displaystyle{\begin{eqnarray}\textcolor{green}{dx=\frac{1}{4}dt}\end{eqnarray}}\)
以上から、
\(\sqrt{4x+1}=t\)
\(\displaystyle{\textcolor{green}{dx=\frac{1}{4}dt}}\)
なので、もとの不定積分は
\(\displaystyle{\int{\sqrt{4x+1}}\textcolor{green}{dx}=\int{\sqrt{t}・\textcolor{green}{\frac{1}{4}dt}}}\)
上式を計算していくと、
\(\displaystyle{\begin{eqnarray}\int\left\{\frac{1}{4}\sqrt{t}\right\}dt&=&\frac{1}{4}\int{t^{\frac{1}{2}}}dt\\\\&=&\frac{1}{4}・\frac{1}{\frac{1}{2}+1}・t^{\frac{1}{2}+1}+C\\\\&=&\frac{1}{4}・\frac{1}{\frac{3}{2}}・t^{\frac{3}{2}}+C\\\\&=&\frac{1}{4}・\frac{2}{3}・t^1t^{\frac{1}{2}}+C\\\\&=&\frac{1}{6}t\sqrt{t}+C\end{eqnarray}}\)
ここで、\(t=4x+1\)なのでこれを代入すると
\(\displaystyle{\begin{eqnarray}&&\frac{1}{6}t\sqrt{t}+C\\\\=&&\frac{1}{6}(4x+1)\sqrt{4x+1}+C\end{eqnarray}}\)
となります。
2) \(\sin{3x}\)の不定積分
\(\int{\sin(3x)}dx\)において、\(t=3x\)とすると\(\sin(3x)=\sin{t}\)
また、
\(\displaystyle{t=3x\Leftrightarrow{x=\frac{1}{3}t}}\)
より、
\(\displaystyle{\frac{dx}{dt}=\frac{1}{3}}\)
ここで、形式的に上辺の両辺に\(dt\)を掛けて
\(\displaystyle{\textcolor{green}{dx=\frac{1}{3}dt}}\)
以上から、
\(\sin(3x)=\sin{t}\)
\(\displaystyle{\textcolor{green}{dx=\frac{1}{3}dt}}\)
なので、もとの不定積分は
\(\displaystyle{\int{\sin(3x)}\textcolor{green}{dx}=\int{\sin{t}}・\textcolor{green}{\frac{1}{3}dt}}\)
上式を計算していくと
\(\displaystyle{\begin{eqnarray}\int\left(\frac{1}{3}\sin{t}\right)dt&=&\frac{1}{3}\int{\sin{t}}dt\\\\&=&\frac{1}{3}・(-\cos{t})+C\\\\&=&-\frac{1}{3}\cos{t}+C\end{eqnarray}}\)
ここで、\(t=3x\)なのでこれを代入すると
\(\displaystyle{-\frac{1}{3}\cos{t}+C=-\frac{1}{3}\cos(3x)+C}\)
となります。
3) \(x\sqrt{2-x}\)の不定積分
\(\displaystyle{\int{x\sqrt{2-x}}dx}\)において、\(t=\sqrt{2-x}\)とおきます。
\(t=\sqrt{2-x}\)の両辺を2乗して、\(x\)について解くと
\(\displaystyle{\begin{eqnarray}&&t^2=2-x\\\\\Leftrightarrow&&x=2-t^2\end{eqnarray}}\)
これを\(t\)で微分すると
\(\displaystyle{\frac{dx}{dt}=-2t}\)
形式的に両辺に\(dt\)を掛けると
\(\textcolor{green}{dx=-2tdt}\)
また、\(x=2-t^2\)から
\(\displaystyle{x\sqrt{2-x}=(2-t^2)・t}\)
よって、求める不定積分は
\(\displaystyle{\begin{eqnarray}\int{x\sqrt{2-x}}\textcolor{green}{dx}&=&\int{(2-t^2)・t・\textcolor{green}{(-2)dt}}\\\\&=&\int{-2(2t^2-t^4)}dt\\\\&=&2\int{t^4-2t^2}dt\\\\&=&2(\frac{1}{5}t^5-\frac{2}{3}t^3)+C\\\\&=&\frac{2}{15}(3t^5-10t^3)+C\\\\&=&\frac{2}{15}t^3(3t^2-10)+C\end{eqnarray}}\)
\(t=\sqrt{2-x}\)なのでこれを代入すると
\(\displaystyle{\begin{eqnarray}&&\frac{2}{15}t^3(3t^2-10)+C\\\\=&&\frac{2}{15}(2-x)\sqrt{2-x}\left\{3(2-x)-10\right\}+C\\\\=&&-\frac{2}{15}(2-x)(3x+4)\sqrt{2-x}+C\end{eqnarray}}\)
となります。
\(\displaystyle{\underline{{f(g(x))g'(x)}{\bf{の不定積分}}}}\)
上で解説した置換積分の公式
\(\displaystyle{\int{f(x)}dx=\int{f(g(x))g'(x)}dt (x=g(t))}\)
において、左辺と右辺を入れ替えて、積分変数\(t\)を\(x\)に、\(x\)を\(u\)に変えると
\(\displaystyle{\textcolor{red}{\int{f(g(x))g'(x)}dx=\int{f(u)}du (g(x)=u)}}\)
となります。
上式も特に覚える必要はないですが、意味としては\(du=g'(x)dx\)となる\(u\)を上手にみつけると、\(f(g(x))g'(x)dx\)の\(g'(x)dx\)部分が\(du\)となって計算しやすくなりますよ、というものになります。
そのために、微分して\(g'(x)\)となるような\(g(x)\)を\(u\)とおきましょうということです。
※\(u=g(x)\)から\(\displaystyle{\frac{du}{dx}=g'(x)}\)なので、形式的に両辺に\(dx\)を掛けると\(\textcolor{green}{du=g'(x)dx}\)
これより、
\(\displaystyle{\int{f(g(x)\textcolor{green}{g'(x)dx})}=\int{f(u)}\textcolor{green}{du}}\)
となります。
実際に計算例をみてみると、分かりやすいと思います。
例) \(\displaystyle{\int{\cos^2{x}\sin{x}}dx}\)
\(\cos{x}=u\)とおくと、
\(\displaystyle{\frac{du}{dx}=-\sin{x}}\)
から、形式的に両辺に\(-dx\)を掛けて
\(\textcolor{green}{-du=\sin{x}dx}\)
(これから、\(\cos^2{x}\sin{x}dx\)の\(\sin{x}dx\)が消えてくれてこの部分が\(-du\)となってくれる)
また、\(u=\cos{x}\)なので求める不定積分は
\(\displaystyle{\begin{eqnarray}\int{\cos^2{x}\textcolor{green}{\sin{x}dx}}&=&\int{u^2\textcolor{green}{(-du)}}\\\\&=&-\int{u^2}du\\\\&=&-\frac{1}{3}u^3+C\end{eqnarray}}\)
\(u=\cos{x}\)なので、もとにもどして
\(\displaystyle{-\frac{1}{3}u^3+C=-\frac{1}{3}\cos^3{x}+C}\)
となります。
また、
\(\displaystyle{\int{f(g(x))g'(x)}dx=\int{f(u)}du (g(x)=u)}\)
において、\(\displaystyle{f(u)=\frac{1}{u}}\)とすると\(u=g(x)\)なので
\(\displaystyle{\begin{eqnarray}f(u)&=&\frac{1}{u}\\\\&=&\frac{1}{g(x)}\\\\&=&f(g(x))\end{eqnarray}}\)
となります。
上記のことを用いると、
\(\displaystyle{\begin{eqnarray}\int{f(g(x))g'(x)}dx&=&\int{\frac{g'(x)}{g(x)}}dx\\\\&=&\int{f(u)}du\\\\&=&\int{\frac{1}{u}}du\\\\&=&\log|u|+C\\\\&=&\log|g(x)|+C\end{eqnarray}}\)
よって、次のことがいえます。
\(\displaystyle{\textcolor{red}{\int{\frac{g'(x)}{g(x)}}dx=\log|g(x)|+C}}\)
上記公式の意味も前回のものと同様、\(du=g'(x)dx\)となる\(u\)を上手にみつけると、\(f(g(x))g'(x)dx\)の\(g'(x)dx\)部分が\(du\)となるので、微分して\(g'(x)\)となるような\(g(x)\)を\(u\)とおきましょう、というものになります。
計算例をみると、わかりやすいかと思います。
例) \(\int{\tan{x}}dx\)
\(\displaystyle{\tan{x}=\frac{\sin{x}}{\cos{x}}}\)なので、与式は
\(\displaystyle{\int{\tan{x}}dx=\int{\frac{\sin{x}}{\cos{x}}}dx}\)
ここで、\(\cos{x}\)を微分すると\(\sin{x}\)となって、与式の\(\sin{x}dx\)が消えてくれそうなので、\(u=\cos{x}\)とおくと
\(\displaystyle{\frac{du}{dx}=-\sin{x}}\)
形式的に両辺に\(-dx\)を掛けて
\(\textcolor{green}{-du=\sin{x}dx}\)
これと、\(u=\cos{x}\)から与式は
\(\displaystyle{\begin{eqnarray}\int{\tan{x}}dx&=&\int{\frac{\textcolor{green}{\sin{x}}}{\cos{x}}}\textcolor{green}{dx}\\\\&=&\int{\frac{1}{u}}・(\textcolor{green}{-du})\\\\&=&-\int{\frac{1}{u}}du\\\\&=&-\log|u|+C\end{eqnarray}}\)
\(u=\cos{x}\)なので、もとにもどして
\(-\log|u|+C=-\log|\cos{x}|+C\)
となります。
1-4.部分積分
積の微分公式から
\(\displaystyle{\left\{f(x)g(x)\right\}’=f'(x)g(x)+f(x)g'(x)}\)
よって、\(f(x)g(x)\)は\(f'(x)g(x)+f(x)g'(x)\)の原始関数であるといえます。
このことから、
\(\displaystyle{f(x)g(x)=\int{f'(x)g(x)}dx+\int{f(x)g'(x)}dx}\)
上式の\(\displaystyle{\int{f'(x)g(x)}dx}\)を左辺に移項すると、次の部分積分法の公式が成り立ちます。
\(\displaystyle{\textcolor{red}{\int{f(x)g'(x)}dx=f(x)g(x)-\int{f'(x)g(x)}dx}}\)
上記部分積分の公式のポイントとしては、\(f'(x)\)が簡単になるように\(f(x)\)を選ぶ、または\(f'(x)g(x)\)が簡単になるように\(f(x)\)と\(g(x)\)を選ぶということです。
計算例で具体的にみていきます。
例1) \(\displaystyle{\int{x\cos{x}}dx}\)
部分積分の公式において、\(f(x)=x\)とすると\(f'(x)=1\)となって\(\int{f'(x)g(x)}dx\)の項が簡単になりそうです。
また、\(f(x)=x\)とみるとき\(g'(x)=\cos{x}\)とみるので
\(\displaystyle{\begin{eqnarray}g(x)&=&\int{g'(x)}dx\\\\&=&\int{\cos{x}}dx\\\\&=&\sin{x}+C\end{eqnarray}}\)
以上より
\(f(x)=x\)
\(g'(x)=\cos{x}\)
\(g(x)=\sin{x}\)
とみると、部分積部の公式
\(\displaystyle{\textcolor{red}{\int{f(x)g'(x)}dx=f(x)g(x)-\int{f'(x)g(x)}dx}}\)
から、与式は
\(\displaystyle{\begin{eqnarray}&&\int{x\cos{x}}dx\\\\=&&\int{x(\sin{x})’}dx\\\\=&&x\sin{x}-\int{(x)’・\sin{x}}dx\\\\=&&x\sin{x}-\int{\sin{x}}dx\\\\=&&x\sin{x}+\cos{x}+C\end{eqnarray}}\)
となります。
例2) \(\displaystyle{\int{x\log{x}}dx}\)
\(\log{x}\)を微分すると
\(\displaystyle{(\log{x})’=\frac{1}{x}}\)
となるので、公式の\(f'(x)g(x)\)部分で\(x\)と打ち消しあってくれそうです。
なので\(f(x)=\log{x}\)とみてみます。
このとき、\(g'(x)=x\)とみるので
\(\displaystyle{\begin{eqnarray}g(x)&=&\int{g'(x)}dx\\\\&=&\int{x}dx\\\\&=&\frac{1}{2}x^2+C\end{eqnarray}}\)
から、
\(\displaystyle{g(x)=\frac{1}{2}x^2}\)
とみます。
以上から、
\(f(x)=\log{x}\)
\(\displaystyle{g(x)=\frac{1}{2}x^2}\)
とみると、部分積分の公式
\(\displaystyle{\textcolor{red}{\int{f(x)g'(x)}dx=f(x)g(x)-\int{f'(x)g(x)}dx}}\)
から、
\(\displaystyle{\begin{eqnarray}&&\int{x\log{x}}dx\\\\=&&\int{\log{x}\left(\frac{1}{2}x^2\right)’}dx\\\\=&&\log{x}・\left(\frac{1}{2}x^2\right)-\int{(\log{x})’・\left(\frac{1}{2}x^2\right)}dx\\\\=&&\frac{1}{2}x^2\log{x}-\int{\frac{1}{x}・\left(\frac{1}{2}x^2\right)}dx\\\\=&&\frac{1}{2}x^2\log{x}-\frac{1}{2}\int{x}dx\\\\=&&\frac{1}{2}x^2\log{x}-\frac{1}{2}\left(\frac{1}{2}x^2\right)+C\\\\=&&\frac{1}{2}x^2\log{x}-\frac{1}{4}x^2+C\\\\=&&\frac{2}{4}x^2\log{x}-\frac{1}{4}x^2+C\\\\=&&\frac{1}{4}x^2(2\log{x}-1)+C\end{eqnarray}}\)
となります。
1-5.三角関数に関する積分
三角関数に関する積分では、2倍角の公式や積和の公式を使うことがよくあります。
三角関数の公式についてはこちらも参考にしてください
→三角関数の公式
2倍角の公式は以下のようなものがあります。
\(\displaystyle{\sin^2\alpha=\frac{1-\cos{2\alpha}}{2}}\)
\(\displaystyle{\cos^2\alpha=\frac{1+\cos{2\alpha}}{2}}\)
\(\displaystyle{\sin\alpha\cos\alpha=\frac{\sin{2\alpha}}{2}}\)
積和の公式には以下のようなものがあります。
\(\displaystyle{\sin\alpha\cos\beta=\frac{1}{2}\left\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\right\}}\)
\(\displaystyle{\cos\alpha\cos\beta=\frac{1}{2}\left\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\right\}}\)
\(\displaystyle{\sin\alpha\sin\beta=-\frac{1}{2}\left\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\right\}}\)
これらを用いた計算例をみていきます。
例1) \(\displaystyle{\int{\sin^2x}dx}\)
2倍角の公式を用いて式変形をすると
\(\displaystyle{\begin{eqnarray}\int{\sin^2x}dx&=&\int{\frac{1}{2}(1-\cos2x)}dx\\\\&=&\frac{1}{2}\left\{\int{(1-\cos2x)}dx\right\}\end{eqnarray}}\)
ここで、\(\int{\cos2x}dx\)について置換積分法を用いて、\(u=2x\)とおくと\(\displaystyle{x=\frac{1}{2}u}\)より\(\displaystyle{\frac{dx}{du}=\frac{1}{2}}\)
これより、形式的に
\(\displaystyle{dx=\frac{1}{2}du}\)
となるので
\(\displaystyle{\begin{eqnarray}\int{\cos2x}dx&=&\int{\cos{u}・\frac{1}{2}du}\\\\&=&\frac{1}{2}\int{\cos{u}}du\\\\&=&\frac{1}{2}\sin{u}+C_1\\\\&=&\frac{1}{2}\sin2x+C_1 (C_1は積分定数)\end{eqnarray}}\)
以上から与式は
\(\displaystyle{\begin{eqnarray}\int{\sin^2x}dx&=&\frac{1}{2}\left\{\int{(1-\cos2x)}dx\right\}dx\\\\&=&\frac{1}{2}\left\{\int{1}dx-\int{\cos2x}dx\right\}\\\\&=&\frac{1}{2}(x-\frac{1}{2}\sin2x)+C\\\\&=&\frac{1}{2}x-\frac{1}{4}\sin2x+C\end{eqnarray}}\)
となります。
例2) \(\displaystyle{\int{\sin2x\cos3x}dx}\)
与式を、\(\sin\)と\(\cos\)の積→和の公式を用いて変形すると
\(\displaystyle{\begin{eqnarray}&&\int{\sin2x\cos3x}dx\\\\=&&\int{\frac{1}{2}\left\{\sin(2x+3x)+\sin(2x-3x)\right\}}dx\\\\=&&\frac{1}{2}\int\left\{\sin5x+\sin(-x)\right\}dx\\\\=&&\frac{1}{2}\int(\sin5x-\sin{x})dx\end{eqnarray}}\)
上式を、例1と同様にして置換積分法を用いて計算すると
\(\displaystyle{\begin{eqnarray}&&\frac{1}{2}\int(\sin5x-\sin{x})dx\\\\=&&\frac{1}{2}\left\{\int{\sin5x}dx-\int{\sin{x}}dx\right\}\\\\=&&\frac{1}{2}(-\frac{1}{5}\cos5x+\cos{x})+C\\\\=&&-\frac{1}{10}\cos5x+\frac{1}{2}\cos{x}+C\end{eqnarray}}\)
となります。
2.定積分
2-1.復習
区間\([a,b]\)で連続な関数\(f(x)\)の原始関数の1つを\(F(x)\)とするとき、
\(\displaystyle{\int_a^b{f(x)}dx}=\left[F(x)\right]_a^b=F(b)-F(a)\)
※区間\([a,b]\)は\(a\le{x}\le{b}\)のこと
\(a\)をこの定積分の下端、\(b\)を上端といい、定積分\(\displaystyle{\int_a^b{f(x)}dx}\)を求めることを\(f(x)\)を\(a\)から\(b\)まで積分するといいます。
定積分\(\displaystyle{\int_a^b{f(x)}dx}\)は区間\([a,b]\)で常に\(f(x)\ge0\)のとき、曲線\(y=f(x)\)と\(x\)軸および2直線\(x=a,x=b\)で囲まれた部分の面積を表します。
\(\underline{\bf{定積分の性質}}\)
「積分法」で解説しましたが、定積分の性質には以下のようなものがあります。
\(\displaystyle{\int_a^b{kf(x)}dx=k\int_a^b{f(x)}dx (kは定数)}\)
\(\displaystyle{\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^b{f(x)}dx+\int_a^b{g(x)}dx}\)
\(\displaystyle{\int_a^b\left\{f(x)-g(x)\right\}dx=\int_a^b{f(x)}dx-\int_a^b{g(x)}dx}\)
\(\displaystyle{\int_a^a{f(x)}dx=0}\)
\(\displaystyle{\int_b^a{f(x)}dx=-\int_a^b{f(x)}dx}\)
\(\displaystyle{\int_a^b{f(x)}dx=\int_a^c{f(x)}dx+\int_c^b{f(x)}dx}\)
2-2.絶対値のついた関数の定積分
関数\(f(x)\)が\(a{\le}x{\le}c)で(f(x)\ge0\)、\(c{\le}x{\le}b\)で\(f(x)\le0\)のとき、絶対値のついた関数\(|f(x)|\)を\(a\)から\(b\)まで積分するには
\(\displaystyle{\int_a^b{|f(x)|}dx=\int_a^c{f(x)}dx+\int_c^b{\left\{-f(x)\right\}}dx}\)
のように、区間を分けて行います。
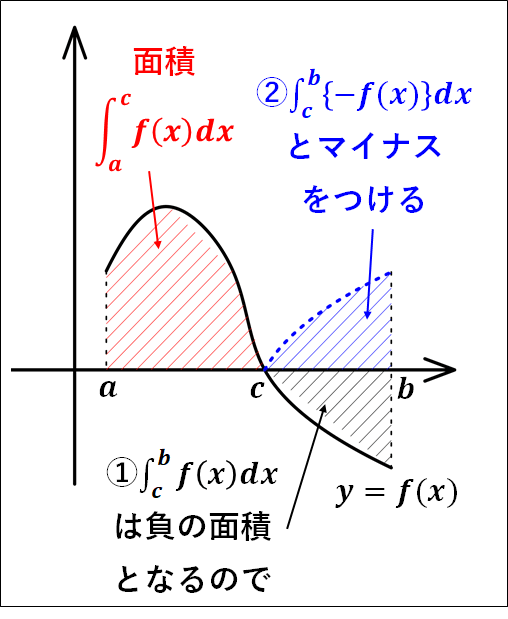
上図から、全体の面積は赤色部分と青色部分を足して
\(\displaystyle{\textcolor{red}{\int_a^c{f(x)}dx}+\textcolor{blue}{\int_c^b{\left\{-f(x)\right\}}dx}}\)
となります。
例) \(\displaystyle{\int_0^{2\pi}{|\sin{x}|}dx}\)
\(y=\sin{x}\)のグラフは、\(0{\le}x{\le}\pi\)で\(\sin{x}\ge0\)、\(\pi{\le}x{\le}2\pi\)で\(\sin{x}\le0\)となります。
よって、\(y=|\sin{x}|\)のグラフは、\(\sin{x}\le0\)の部分を\(x\)軸に関して折り返した以下のようになります。
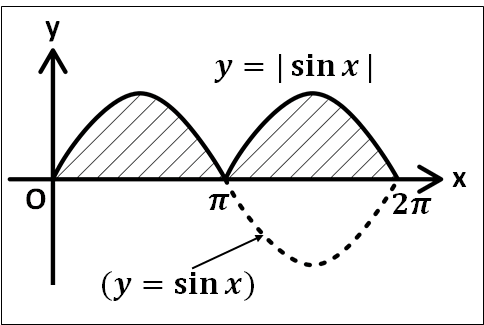
求める定積分の値は、上図の斜線部となります。
したがって、
\(\displaystyle{\begin{eqnarray}\int_0^{2\pi}{|\sin{x}|}dx&=&\int_0^{\pi}{\sin{x}}dx+\int_{\pi}^{2\pi}{(-\sin{x})}dx\\\\&=&\left[-\cos{x}\right]_0^{\pi}+\left[\cos{x}\right]_{\pi}^{2\pi}\\\\&=&(1+1)+(1+1)\\\\&=&4\end{eqnarray}}\)
となります。
2-3.置換積分
\(F(x)\)を\(f(x)\)の原始関数として、\(x\)が微分可能な関数\(g(t)\)を用いて\(x=g(t)\)と表されるとき、合成関数の微分法によって、
\(\displaystyle{\frac{d}{dt}F(g(t))=f(g(t))・g'(t)}\)
となります。
\(a=g(\alpha)\)、\(b=g(\beta)\)とすると、
\(\displaystyle{\begin{eqnarray}\int_{\alpha}^{\beta}{f(g(t))・g'(t)}dt&=&\left[F(g(t))\right]_{\alpha}^{\beta}\\\\&=&F(g(\beta))-f(g(\alpha))\\\\&=&F(b)-F(a)\\\\&=&\int_a^b{f(x)}dx\end{eqnarray}}\)
これより、次のことがいえます。
\(x=g(t)\)とおくとき、\(a=g(\alpha),b=g(\beta)\)ならば
\(\displaystyle{\textcolor{red}{\int_a^b{f(x)}dx=\int_{\alpha}^{\beta}{f(g(t))・g'(t)}dt}}\)
※\(x=g(t)\)とおくと、\(t\)の定義域による\(g(t)\)の値域が\(x\)の値となるので、積分変数を\(t\)から\(x\)にする際には積分区間も\(t\)から\(x\)に変換する必要があります。
計算例で具体的に感覚をつかんでください。
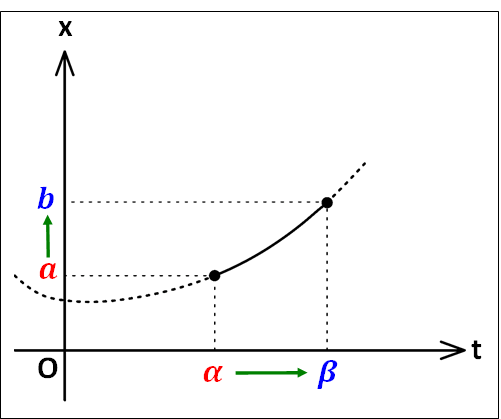
例) \(\displaystyle{\int_1^2{x(x+1)^2}dx}\)
\(t=x+1\)とおくと、
\(\displaystyle{\begin{eqnarray}t=x+1\Leftrightarrow{x}=t-1\end{eqnarray}}\)
また\(t\)で微分して
\(\displaystyle{\frac{dx}{dt}=1}\)
より、形式的に両辺に\(dt\)を掛けて\(\textcolor{green}{dx=dt}\)
積分区間については、\(t=x+1\)から
\(\textcolor{blue}{x:1\to2}\)のとき\(\textcolor{red}{t:2\to3}\)
(※\(x=1,x=2\)をそれぞれ\(t=x+1\)に代入した)
以上から、与式は
\(\displaystyle{\begin{eqnarray}\int_{\textcolor{blue}{1}}^{\textcolor{blue}{2}}{x(x-1)^2}\textcolor{green}{dx}&=&\int_{\textcolor{red}{2}}^{\textcolor{red}{3}}{(t-1)t^2}\textcolor{green}{dt}\\\\&=&\int_2^3{(t^3-t^2)}dt\\\\&=&\left[\frac{1}{4}t^4-\frac{1}{3}t^3\right]_2^3\\\\&=&\left(\frac{81}{4}-9\right)-\left(\frac{16}{4}-\frac{8}{3}\right)\\\\&=&\frac{81}{4}+\frac{8}{3}-9+4\\\\&=&\frac{243+32-156}{12}\\\\&=&\frac{119}{12}\end{eqnarray}}\)
となります。
次に、ある程度解法が決まっている置換積分について紹介していきます。
\(\underline{{x=a\sin{\theta}}{\bf{とおく定積分}}}\)
i) \(\displaystyle{\int_0^a{\sqrt{a^2-x^2}}dx (a{\bf{を正の実数とする)}}}\)
\(x=a\sin{\theta}\)とおくと、\(\displaystyle{\frac{dx}{d{\theta}}=a\cos{\theta}}\)から、形式的に\(\textcolor{green}{dx=a\cos{\theta}d{\theta}}\)
また、
\(x=0\)のとき、\(0=a\sin\theta\)から\(\sin\theta=0\)。よって、\(\theta=0\)
\(x=a\)のとき、\(a=a\sin\theta\)から\(1=\sin\theta\)。よって、\(\displaystyle{\theta=\frac{\pi}{2}}\)
なので、\(\textcolor{blue}{x:0\to{a}}\)のとき、\(\displaystyle{\textcolor{red}{\theta:0\to\frac{\pi}{2}}}\)
この\(\theta\)の範囲で、\(\cos\theta\ge0\)となります。
\(\sqrt{a^2-x^2}\)について、\(x=a\sin\theta\)なので
\(\displaystyle{\begin{eqnarray}\sqrt{a^2-x^2}&=&\sqrt{a^2-a^2\sin^2\theta}\\\\&=&\sqrt{a^2(1-\sin^2\theta)}\\\\&=&\sqrt{a^2\cos^2\theta} (∵\sin^2\theta+\cos^2\theta=1)\\\\&=&a\cos\theta\end{eqnarray}}\)
以上から与式は、
\(\displaystyle{\begin{eqnarray}&&\int_{\textcolor{blue}{0}}^{\textcolor{blue}{a}}{\sqrt{a^2-x^2}}\textcolor{green}{dx}\\\\=&&\int_{\textcolor{red}{0}}^{\textcolor{red}{\frac{\pi}{2}}}{a\cos\theta・\textcolor{green}{a\cos\theta{d}\theta}}\\\\=&&a^2\int_0^{\frac{\pi}{2}}{\cos^2\theta}d\theta\\\\=&&a^2\int_0^{\frac{\pi}{2}}{\frac{1+\cos{2\theta}}{2}}d\theta (←2倍角の公式から)\\\\=&&\frac{a^2}{2}\int_0^{\frac{\pi}{2}}{(1+\cos{2\theta})}d\theta\\\\=&&\frac{a^2}{2}\left[\theta+\frac{1}{2}\sin{2\theta}\right]_0^{\frac{\pi}{2}}\\\\=&&\frac{a^2}{2}\left(\frac{\pi}{2}\right)\\\\=&&\frac{\pi}{4}a^2\end{eqnarray}}\)
となります。
ii) \(\displaystyle{\int_0^a{\frac{1}{\sqrt{a^2-x^2}}}dx}\)
\(x=a\sin\theta\)とおくと、\(\displaystyle{\frac{dx}{d\theta}=a\cos\theta}\)より形式的に\(\textcolor{green}{dx=a\cos\theta{d}\theta}\)
また、iのときと同様に
\(\textcolor{blue}{x:0\to{a}}\)のとき\(\displaystyle{\textcolor{red}{t:0\to\frac{\pi}{2}}}\)
またこの範囲で\(\cos\theta\ge0\)となり、
\(\displaystyle{\begin{eqnarray}\sqrt{a^2-x^2}&=&\sqrt{a^2-a^2\sin^2\theta}\\\\&=&a\cos\theta\end{eqnarray}}\)
よって、
\(\displaystyle{\begin{eqnarray}\int_{\textcolor{blue}{0}}^{\textcolor{blue}{a}}{\frac{1}{\sqrt{a^2-x^2}}}\textcolor{green}{dx}&=&\int_{\textcolor{red}{0}}^{\textcolor{red}{\frac{\pi}{2}}}{\frac{1}{a\cos\theta}・\textcolor{green}{a\cos\theta{d\theta}}}\\\\&=&\int_0^{\frac{\pi}{2}}d\theta\\\\&=&\left[\theta\right]_0^{\frac{\pi}{2}}\\\\&=&\frac{\pi}{2}\end{eqnarray}}\)
となります。
これまで見てきたことから、
☆\(\textcolor{red}{\underline{{\sqrt{a^2-x^2}}{\bf{の形では}}{x=a\sin\theta}{\bf{とおく}}}}\)
(\(a\)は文字ではなく数字のときでも上記のようにおく)
\(\underline{{x=a\tan\theta}{\bf{とおく定積分}}}\)
i) \(\displaystyle{\int_1^{\sqrt{3}}\frac{1}{x^2+3}dx}\)
\(x=\sqrt{3}\tan\theta\)とおくと、\(\displaystyle\frac{dx}{d\theta}=\frac{\sqrt{3}}{\cos^2\theta}\)より形式的に\(\displaystyle{\textcolor{green}{dx=\frac{\sqrt{3}}{\cos^2\theta}d\theta}}\)
積分区間については、
\(x=1\)のとき、\(\displaystyle{\tan\theta=\frac{1}{\sqrt{3}}}\)から\(\displaystyle{\theta=\frac{\pi}{6}}\)
\(x=\sqrt{3}\)のとき、\(\tan\theta=1\)から\(\displaystyle{\theta=\frac{\pi}{4}}\)
よって、
\(\textcolor{blue}{x:1\to\sqrt{3}}\)のとき、\(\displaystyle{\textcolor{red}{\theta:\frac{\pi}{6}\to\frac{\pi}{4}}}\)
また、\(x=\sqrt{3}\tan\theta\)とおいているので
\(\displaystyle{\begin{eqnarray}\frac{1}{x^2+3}&=&\frac{1}{3\tan^2\theta+3}\\\\&=&\frac{1}{3}・\frac{1}{\tan^2\theta+1}\\\\&=&\frac{1}{3}\cos^2\theta \left(∵\tan^2\theta+1=\frac{1}{\cos^2\theta}\right)\end{eqnarray}}\)
以上から与式は
\(\displaystyle{\begin{eqnarray}\int_{\textcolor{blue}{1}}^{\textcolor{blue}{\sqrt{3}}}{\frac{1}{x^2+3}}\textcolor{green}{dx}&=&\int_{\textcolor{red}{\frac{\pi}{6}}}^{\textcolor{red}{\frac{\pi}{4}}}{\frac{1}{3}\cos^2\theta\textcolor{green}{\frac{\sqrt{3}}{\cos^2\theta}d\theta}}\\\\&=&\frac{\sqrt{3}}{3}\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}d\theta\\\\&=&\frac{\sqrt{3}}{3}\left[\theta\right]_{\frac{\pi}{6}}^{\frac{\pi}{4}}\\\\&=&\frac{\sqrt{3}}{3}\left(\frac{\pi}{4}-\frac{\pi}{6}\right)\\\\&=&\frac{\sqrt{3}}{3}・\frac{3-2}{12}\pi\\\\&=&\frac{\sqrt{3}}{3}・\frac{1}{12}\pi\\\\&=&\frac{\sqrt{3}}{36}\pi\end{eqnarray}}\)
となります。
これまで見てきたことから、
☆\(\displaystyle{\textcolor{red}{\underline{{\frac{1}{x^2+a^2} (a\gt0)}{\bf{の形では}}{x=a\tan\theta}{\bf{とおく}}}}}\)
2-4.偶数関数と奇関数の定積分
関数\(f(x)\)において、
\(f(-x)=f(x)\)が常に成り立つとき、この関数を偶関数といい、グラフは\(y\)軸に関して対称となります。
\(f(-x)=-f(x)\)が常に成り立つとき、この関数を奇関数といい、グラフは原点に関して対称となります。
例として、三角関数においては、\(f(x)=\cos\theta\)は偶関数、\(f(x)=\sin\theta\)は奇関数となります。
三角関数についてはこちらで解説していますので、グラフの形と\(-\theta\)に関する公式を確認してみてください。
→三角関数のグラフ
→三角関数の公式
関数\(f(x)\)が偶関数または奇関数のとき、次のことが成り立ちます。
1.偶関数\(f(x)\)について
\(\displaystyle{\int_{-a}^a{f(x)}dx=2\int_0^a{f(x)}dx}\)
2.奇関数\(f(x)\)について
\(\displaystyle{\int_{-a}^a{f(x)}dx=0}\)
\(\underline{\bf{証明}}\)
定積分の性質から
\(\displaystyle{\int_{-a}^a{f(x)}dx=\int_{-a}^0{f(x)}dx+\int_0^a{f(x)}dx}\)
\(\displaystyle{\int_{-a}^0{f(x)}dx}\)において、\(x=-t\)とおくと、\(dx=-dt\)、\(x:-a\to0\)のとき\(t:a\to0\)なので
\(\displaystyle{\begin{eqnarray}\int_{-a}^0{f(x)}dx&=&\int_a^0{-f(-t)}dt\\\\&=&\int_0^a{f(-t)}dt\\\\&=&\int_0^a{f(-x)}dx\end{eqnarray}}\)
よって、
\(\displaystyle{\int_{-a}^a{f(x)}dx=\int_0^a{\{f(-x)+f(x)\}}dx}\)
\(f(x)\)が偶関数のとき、\(f(-x)=f(x)\)、奇関数のとき\(f(-x)=-f(x)\)なので、これらを上式に代入すると、偶関数・奇関数における定積分の性質が成り立つことがわかります。
また、定積分は図形の面積を表すのでグラフの形からも直感的にわかると思います。
偶関数については、グラフが\(y\)軸対称なので\(x\)が\(-a\)から\(0\)までの面積と\(0\)から\(a\)までの面積が等しくなるので、\(0\)から\(a\)までの面積の2倍となります。
奇関数に関しては、グラフが原点対称なので、\(x\)が\(-a\)から\(0\)までの面積と\(0\)から\(a\)までの面積ではその正負が逆になります。
よって、面積の絶対値は等しくその正負は逆なので、この二つの面積を足すと\(0\)となります。
例)
\(f(x)=\cos{x}\)は偶関数であるから
\(\displaystyle{\begin{eqnarray}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}{\cos{x}}dx&=&2\int_0^{\frac{\pi}{2}}{\cos{x}}dx\\\\&=&2\left[\sin{x}\right]_0^{\frac{\pi}{2}}\\\\&=&2\end{eqnarray}}\)
\(f(x)=\sin{x}\)は奇関数であるから
\(\displaystyle{\int_{-\pi}^{\pi}{\sin{x}}dx=0}\)
2-5.部分積分
不定積分の部分積分の公式
\(\displaystyle{\int{f(x)g'(x)}dx=f(x)g(x)-\int{f'(x)g(x)}dx}\)
から、定積分の部分積分の公式は次のようになります。
\(\displaystyle{\textcolor{red}{\int_a^b{f(x)g'(x)}dx=\left[f(x)g(x)\right]_a^b-\int_a^b{f'(x)g(x)}dx}}\)
計算例)
\(\displaystyle{\begin{eqnarray}&&\int_0^{\frac{\pi}{2}}{x\cos{x}}dx\\\\=&&\int_0^{\frac{\pi}{2}}{x(\sin{x})’}dx\\\\=&&\left[x\sin{x}\right]_0^{\frac{\pi}{2}}-\int_0^{\frac{\pi}{2}}{(x)’\sin{x}}dx\\\\=&&\frac{\pi}{2}-\int_0^{\frac{\pi}{2}}{\sin{x}}dx\\\\=&&\frac{\pi}{2}-\left[\cos{x}\right]_0^{\frac{\pi}{2}}\\\\=&&\frac{\pi}{2}+(0-1)\\\\=&&\frac{\pi}{2}-1\end{eqnarray}}\)
となります。
3.区分求積法
曲線\(y=f(x)\)と\(x\)軸および、\(x=a,x=b\)で囲まれた部分の面積を考えます。
下図のように区間\([a,b]\)を\(n\)等分し、その分点の座標を\(a\)に近い方から順に、\(x_1,x_2,x_3,\cdots,x_{n-1}\)とします。
また、\(a=x_0 , b=x_n\)とします。
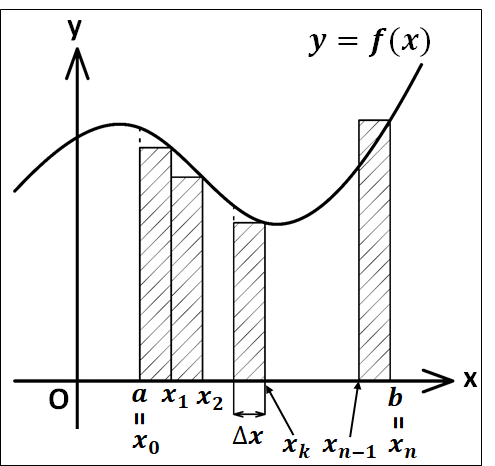
区間\([a,b]\)を\(n\)等分しているので、図の長方形の幅を\(\Delta{x}\)とすると
\(\displaystyle{\Delta{x}=\frac{b-a}{n}}\)
となります。
また、
\(\displaystyle{x_k=a+\frac{b-a}{n}k=a+k\Delta{x}}\)
となる点における長方形の面積は
\(f(x_k)\Delta{x}\)
となります。
※\(x_k\)は、\(x\)の値が\(a\)から幅\(\Delta{x}\)が\(k\)個分進んだ地点の値。
\(x=x_k\)における長方形の面積は、横幅\(\Delta{x}\)、縦幅\(f(x_k)\)の長方形とみなせる。
このことから、図の長方形の面積を全て足したものは
\(\displaystyle{\sum_{k=1}^nf(x_k)\Delta{x}}\)
となります。
※ \(\displaystyle{\sum_{k=1}^nf(x_k)\Delta{x}}\) は、\(f(x_k)\Delta{x}\)の\(k\)に\(k=1,k=2,\cdots,k=n\)を順番に代入していき、それらを全て足し合わせたものという意味。
\(\displaystyle{\sum}\)は合計を表し、「シグマ」と読む。
図中の長方形と\(y=f(x)\)のグラフとの間には隙間が空いていますが、\(n\to\infty\)とすると、\(\Delta{x}\)の幅は限りなく小さくなっていき、隙間はなくなっていきます。
※\(n\to\infty\)とすると、区間\([a,b]\)が無限に分割されていくので、幅は限りなく小さくなる。
また、\(\displaystyle{\Delta{x}=\frac{b-a}{n}}\)からも、\(n\to\infty\)とすると、分母\(n\)が限りなく大きくなるので幅\(\Delta{x}\)は限りなく小さくなっていくことがわかる。
このとき、長方形の面積を全て足したものは、\(y=f(x)\)の曲線と\(x\)軸および\(x=a,x=b\)で囲まれた部分の面積
\(\displaystyle{\int_a^b{f(x)}dx}\)
に限りなく等しくなります。
したがって、次のことがいえます。
\(\displaystyle{\textcolor{red}{\lim_{n\to\infty}\sum_{k=1}^nf(x_k)\Delta{x}=\int_a^b{f(x)}dx}}\)
\(\displaystyle{\textcolor{red}{\left(\Delta{x}=\frac{b-a}{n},x_k=a+k\Delta{x}\right)}}\)
また、上式において\(a=0,b=1\)とすると
\(\displaystyle{\Delta{x}=\frac{1}{n} , x_k=k\Delta{x}=\frac{k}{n}}\)
となるので、上で示した式は
\(\displaystyle{\lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^nf(\frac{k}{n})=\int_0^1{f(x)}dx}\)
となります。
例) \(\displaystyle{\lim_{n\to\infty}\left(\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{n+n}\right)}\)
与式の括弧内を変形して、
\(\displaystyle{\begin{eqnarray}&&\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{n+n}\\\\=&&\frac{1}{n}\left(\frac{1}{1+\frac{1}{n}}+\frac{1}{1+\frac{2}{n}}+\cdots+\frac{1}{1+\frac{n}{n}}\right)\\\\=&&\frac{1}{n}\sum_{k=1}^n\left(\frac{1}{1+\frac{k}{n}}\right)\end{eqnarray}}\)
ここで、
\(\displaystyle{f(x)=\frac{1}{1+x}}\)
とすると、
\(\displaystyle{\begin{eqnarray}&&\lim_{n\to\infty}\left(\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{n+n}\right)\\\\=&&\lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^nf(\frac{k}{n})\\\\=&&\int_0^1{f(x)}dx\\\\=&&\int_0^1{\frac{1}{1+x}}dx\\\\=&&\left[\log(1+x)\right]_0^1\\\\=&&\log2\end{eqnarray}}\)
となります。
4.体積と定積分の関係
4-1.面積と定積分
\(\underline{\bf{復習}}\)
「積分法」の復習となりますが、
区間\([a,b]\)で常に\(f(x)\ge0\)のとき、曲線\(y=f(x)\)と\(x\)軸および2直線\(x=a , x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_a^b{f(x)}dx}\)
区間\([a,b]\)で常に\(f(x)\le0\)のときは
\(\displaystyle{S=\int_a^b{\left\{-f(x)\right\}}dx}\)
で表されます。
区間\(a{\le}x{\le}b\)で常に\(f()x{\ge}g(x)\)のとき、2つの曲線\(y=f(x),y=g(x)\)と\(x\)軸および2直線\(x=a , x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_a^b\left\{f(x)-g(x)\right\}dx}\)
\(\underline{{x=g(y)}{\bf{で表される曲線について}}}\)
\(y\)の関数\(x=g(y)\)で表される曲線については、次のことが成り立ちます。
区間\(c{\le}y{\le}d\)で常に\(g(y)\ge0\)のとき、曲線\(x=g(y)\)と\(y\)軸および2直線\(y=c , y=d\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_c^d{f(y)}dy}\)
で表されます。
例)
\(y=\log{x}\)と\(x\)軸、\(y\)軸および直線\(y=1\)で囲まれた部分の面積\(S\)を求めます。
\(y=\log{x}\)を\(x\)について解くと\(x=e^y\)となります。
常に\(e^y{\ge}0\)であるので、求める面積\(S\)は
\(\displaystyle{\begin{eqnarray}S&=&\int_0^1{e^y}dy\\\\&=&\left[e^y\right]_0^1\\\\&=&e-1\end{eqnarray}}\)
となります。
図示すると、下図のようになります。
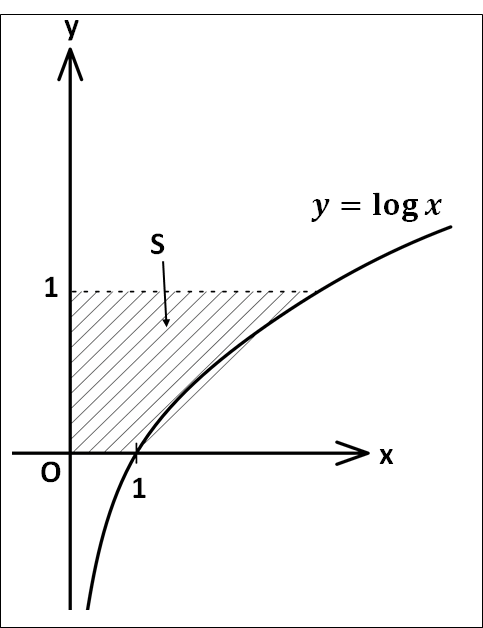
4-2.体積と定積分
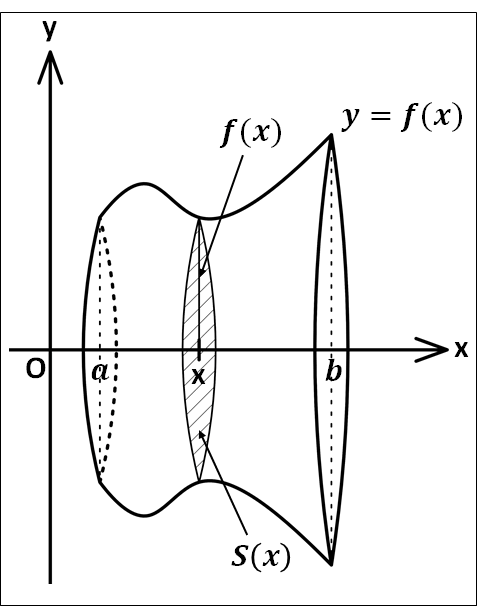
下図のような立体の体積を考えます。
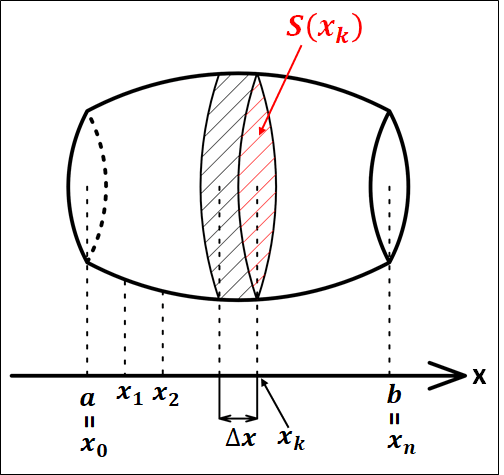
区分求積法と同じように考えて
\(a{\le}x{\le}b\)を\(n\)等分し、その分点の座標を\(a\)に近い方から順に\(x_1,x_2,x_3,\cdots.x_{n-1}\)とします。
\(a=x_0,b=x_n\)として、\(x\)座標が\(x_k\)である部分の面積を\(S(x_k)\)とします。
いま、\(a{\le}x{\le}b\)を\(n\)等分しているので、幅\(\displaystyle{\Delta{x}=\frac{b-a}{n}}\)とすると、分割した部分の全体の体積\(V_n\)は
\(\displaystyle{\begin{eqnarray}V_n&=&S(x_1)\Delta{x}+S(x_2)\Delta{x}+\cdots+S(x_n)\Delta{x}\\\\&=&\sum_{k=1}^n{S(x_k)}\Delta{x}\end{eqnarray}}\)
ここで、\(n\to\infty\)とすると、立体の体積\(V\)が求まります。
以上の内容と、区分求積法で解説した内容から、
\(\displaystyle{\begin{eqnarray}V&=&\lim_{n\to\infty}\sum_{k=1}^n{S(x_k)\Delta{x}}\\\\&=&\int_a^b{S(x)}dx\end{eqnarray}}\)
となります。
したがって、立体の断面積を\(S(x)\)とした際の立体の体積\(V\)は
\(\displaystyle{\textcolor{red}{V=\int_a^b{S(x)}dx (a\lt{b})}}\)
となります。
例) 底面の半径が\(r\)、高さが\(h\)の直円錐の体積\(V\)を求めてみます。
図形を下図のように設定します。
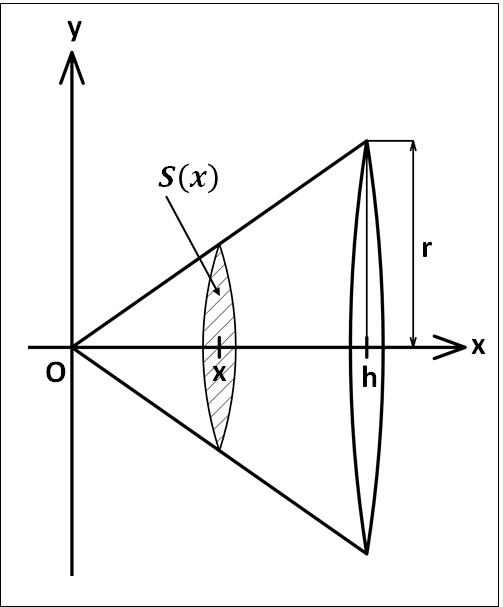
\(x\)座標上の点\(x\)と直角な平面で切り取った部分の面積\(S(x)\)を考えます。
その際に、下図のような直角三角形に注目します。
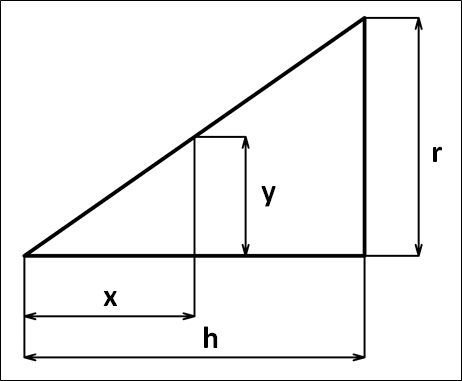
上図直角三角形の相似から、
\(x:y=h:r\)より
\(\displaystyle{yh=xr\Leftrightarrow{y=\frac{r}{h}x}}\)
また、断面積\(S(x)\)は半径\(y\)の円なのでその面積は
\(\displaystyle{S(x)=y^2\pi=\frac{r^2}{h^2}\pi{x^2}}\)
したがって、もとめる体積\(V\)は
\(\displaystyle{\begin{eqnarray}V&=&\int_0^h{s(x)}dx\\\\&=&\int_0^h{\frac{r^2}{h^2}{\pi}x^2}dx\\\\&=&\frac{r^2}{h^2}\pi\left[\frac{1}{3}x^3\right]_0^h\\\\&=&\frac{1}{3}\pi{r^2h}\end{eqnarray}}\)
となります。
※上記では、点\(x\)における\(y\)の値を直角三角形の相似から考えましたが、下記のように直線の式を考えても求めることができます。
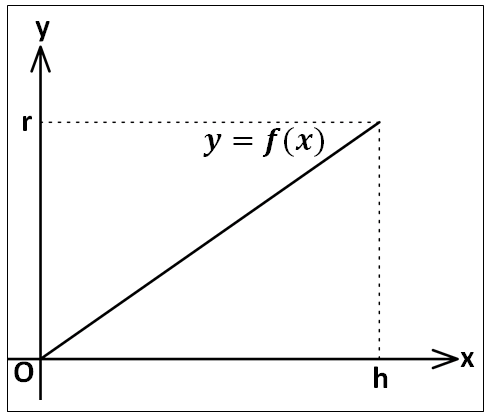
上図の直線\(y=f(x)\)を考えると、原点を通り、傾き\(\displaystyle{\frac{r}{h}}\)の直線であるので、
\(\displaystyle{y=f(x)=\frac{r}{h}x}\)
とも考えることができます。
4-3.回転体の体積
\(\underline{{x}{\bf{軸まわりの体積}}}\)
曲線\(y=f(x)\)と\(x\)軸および2直線\(x=a , x=b\)で囲まれた部分が\(x\)軸の周りに1回転してできる回転体の体積\(V\)を考えます。
そのために、下図のような状況を考えます。
\(x\)軸上の点\(x\)を通り、\(x\)軸に垂直な平面でこの立体を切ると、その断面は半径が\(|f(x)|\)の円となります。
その断面積を\(S(x)\)とすると、
\(\displaystyle{\begin{eqnarray}S(x)&=&\pi|f(x)|^2\\\\&=&\pi\left\{f(x)\right\}^2\end{eqnarray}}\)
となるので、求める体積\(V\)は
\(\displaystyle{\textcolor{red}{\begin{eqnarray}V&=&\pi\int_a^b{\left\{f(x)\right\}^2}dx\\\\&=&\pi\int_a^b{y^2}dx (a\lt{b})\end{eqnarray}}}\)
となります。
例) 半径\(r\)の球の体積\(V\)
求める体積は、下図半円を\(x\)軸の周りに1回転してできる体積となります。
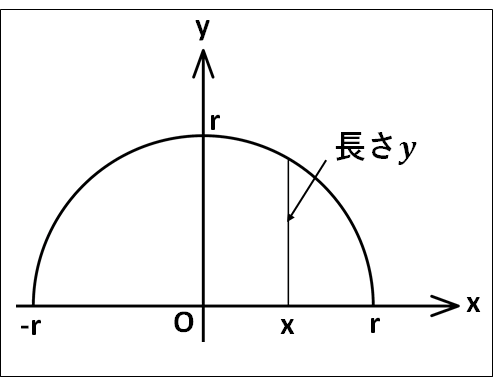
半円の式は、\(x^2+y^2=r^2\)の\(y\gt0\)の部分であるので\(y\)について解くと
\(y=\sqrt{r^2-x^2}\)
となります。
\(x\)座標が\(x\)である部分の回転体の断面積\(S(x)\)は、半径\(y\)の円となるので
\(S(x)=\pi{y^2}\)
であるから、求める体積\(V\)は
\(\displaystyle{\begin{eqnarray}V&=&\int_{-r}^r{\pi{y^2}}dx\\\\&=&\pi\int_{-r}^r(r^2-x^2)dx\\\\&=&\pi\left[r^2x-\frac{1}{3}x^3\right]_{-r}^r\\\\&=&\pi\left\{r^3-\frac{1}{3}r^3-(-r^3+\frac{1}{3}r^3)\right\}\\\\&=&\pi\left(2r^3-\frac{2}{3}r^3\right)\\\\&=&\pi{r^3}\frac{6-2}{3}\\\\&=&\frac{4\pi}{3}r^3\end{eqnarray}}\)
となります。
\(\underline{{y}{\bf{軸まわりの体積}}}\)
曲線\(x=g(y)\)と\(y\)軸および\(y=c , y=d\)で囲まれた部分が\(y\)軸周りに1回転してできる回転体の体積\(V\)を考えます。
そのために、下図のような状況を考えます。
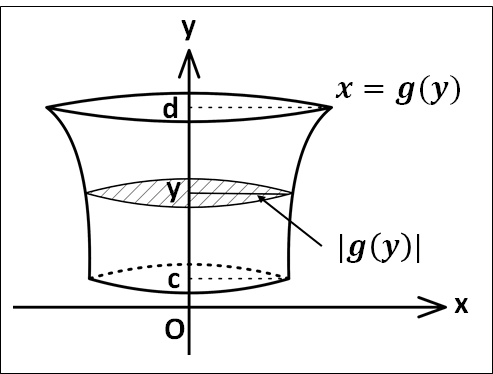
\(x\)軸の周りの回転体の体積と同様に考えて、\(y\)軸の点\(y\)を通り\(y\)軸に垂直な平面で立体を切った体積\(S(y)\)は、半径\(|g(y)|\)の円となるので
\(S(y)=\pi|g(y)|^2=\pi\left\{g(y)\right\}^2\)
よって、求める体積\(V\)は
\(\displaystyle{\textcolor{red}{\begin{eqnarray}V&=&\pi\int_c^d{\left\{g(y)\right\}^2}dy\\\\&=&\pi\int_c^d{x^2}dy (c\lt{d})\end{eqnarray}}}\)
となります。
例)
\(y=x^2-1\)と\(y=4\)で囲まれた部分が\(y\)軸の周りに1回転してできる回転体の体積\(V\)を求めます。
状況を図示すると、概形は下図のようになります。
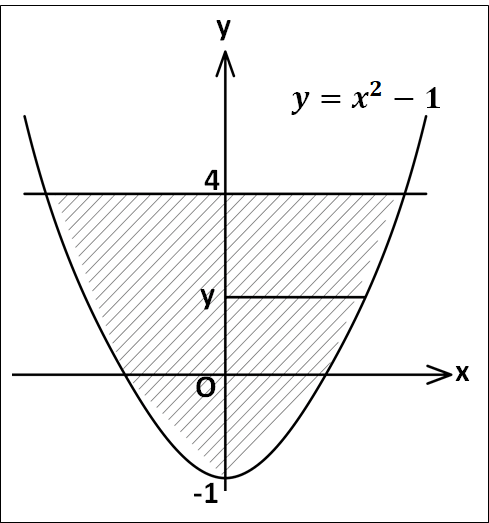
\(y=x^2-1\)より\(x^2=y+1\)
\(y\)軸上の\(y\)である点における断面積\(S(y)\)は
\(S(y)=\pi{x^2}=\pi(y+1)\)
よって求める面積は
\(\displaystyle{\begin{eqnarray}V&=&\pi\int_{-1}^4(y+1)dy\\\\&=&\pi\left\{\frac{1}{2}y^2+y\right\}_{-1}^4\\\\&=&\pi\left\{8+4-\left(\frac{1}{2}-1\right)\right\}\\\\&=&\pi\left(12+\frac{1}{2}\right)\\\\&=&\frac{25}{2}\pi\end{eqnarray}}\)
となります。
今回は以上となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


