投稿日:
【高校物理】指数関数【高校数学】【指数】
\(\require{color}\)
\(\require{cancel}\)
指数関数の基礎的な内容となるので、予習復習したい方向けです。
指数関数のことを分かっているよという方は、読み飛ばして頂いてかまいません。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.指数法則
指数に関して成り立つ法則については、以下の3つとなります。
\(m\) , \(n\)が正の整数のとき
\(a^{\textcolor{red}{m}}×a^{\textcolor{blue}{n}}=a^{\textcolor{red}{m}+\textcolor{blue}{n}} \cdots①\)
\({(a^{\textcolor{red}{m}})}^{\textcolor{blue}{n}}=a^{\textcolor{red}{m}\textcolor{blue}{n}} \cdots②\)
\({(ab)}^{\textcolor{blue}{n}}=a^{\textcolor{blue}{n}}b^{\textcolor{blue}{n}} \cdots③\)
以下に計算例を載せておきます。
例)
\(\underline{\bf{①の例}}\)
\(2^3×2^4=2^{3+4}=2^7\)
\(\underline{\bf{②の例}}\)
\({(2^3)}^4=2^{3×4}=2^{12}\)
\(\underline{\bf{③の例}}\)
\((2×5)^5=2^5×3^5\)
指数が\(0\)のときや、負の整数の累乗は次のように定義します。
\(a\neq0\) , \(n\)を正の整数とするとき、
\(a^0=1 \cdots④\)
\(\displaystyle{a^{-n}=\frac{1}{a^n}}\ \cdots⑤\)
\(⑤\)について、特に
\(\displaystyle{a^{-1}=\frac{1}{a}}\)
以下に計算例を載せておきます。
例)
\(\underline{\bf{④の例}}\)
\(2^0=1\)
\(3^0=1\)
\(4^0=1\)
\(\underline{\bf{⑤の例}}\)
\(\displaystyle{2^{-3}=\frac{1}{2^3}=\frac{1}{8}}\)
\(\displaystyle{10^{-4}=\frac{1}{10^4}=\frac{1}{10000}}\)
以上のことから、一般に指数が整数の場合、次のことが成り立ちます。
\(a\neq0\) , \(b\neq0\)で\(\textcolor{red}{m}\) , \(\textcolor{blue}{n}\)を整数とすると、
\(1. a^{\textcolor{red}{m}}×a^{\textcolor{blue}{n}}=a^{\textcolor{red}{m}+\textcolor{blue}{n}}\)
\(2. \displaystyle{\frac{a^{\textcolor{red}{m}}}{a^{\textcolor{blue}{n}}}=a^{\textcolor{red}{m}}×a^{-\textcolor{blue}{n}}=a^{\textcolor{red}{m}-\textcolor{blue}{n}}}\)
\(3. {(a^{\textcolor{red}{m}})}^{\textcolor{blue}{n}}=a^{\textcolor{red}{m}\textcolor{blue}{n}}\)
\(4. {(ab)}^{\textcolor{blue}{n}}=a^{\textcolor{blue}{n}}b^{\textcolor{blue}{n}}\)
2.累乗根
\(n\)を正の整数とするとき、\(n\)乗して\(a\)になる数を \(a\)の\(n\)乗根といいます。\((x^n=aの解がaのn乗根)\)
また、\(a\)の\(2\)乗根、\(3\)乗根、\(4\)乗根\(\cdots\)を総称して\(a\)の累乗根といいます。
正の数\(a\)の\(n\)乗根のうち正であるものについて考えると、\(y=x^n\)のグラフの概形は以下のようになります。
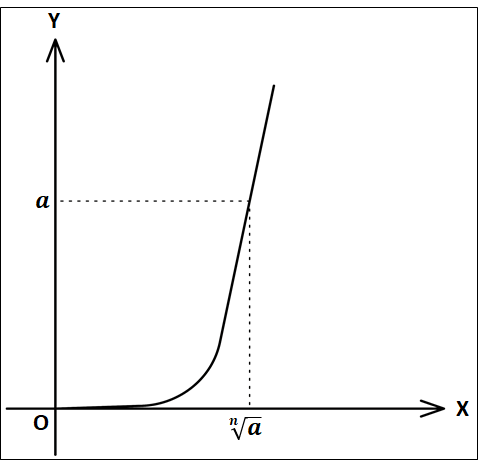
また、\(a\gt0\)のとき
\( \sqrt[\textcolor{blue}{n}] {a}\gt0 \)
\((\sqrt[\textcolor{blue}{n}] {a})^n=a\)
\(\sqrt[\textcolor{blue}{n}]{a^n}=a\)
となります。
グラフから、正の数\(a\)に対して、\(x^{\textcolor{blue}{n}}=a\)を満たす正の数\(x\)がただ1つあることがわかり、この正の数\(x\)を\(\sqrt[\textcolor{blue}{n}]{a}\)で表します。
また、\(\sqrt[\textcolor{blue}{n}]{a}\)の定義から、次の性質があります。
\(a\gt0\) , \(b\gt0\)で\(\textcolor{red}{m}\) , \(\textcolor{blue}{n}\)を正の整数とすると
\(\sqrt[\textcolor{blue}{n}]{a}\sqrt[\textcolor{blue}{n}]{b}=\sqrt[\textcolor{blue}{n}]{ab}\ \cdots①\)
\(\displaystyle{\frac{\sqrt[\textcolor{blue}{n}]{a}}{\sqrt[ \textcolor{blue}{n} ]{b}}=\sqrt[\textcolor{blue}{n}]{\frac{a}{b}}} \cdots②\)
\((\sqrt[\textcolor{blue}{n}]{a})^{\textcolor{red}{m}}=\sqrt[\textcolor{blue}{n}]{a^{\textcolor{red}{m}}} \cdots③\)
\(\displaystyle{\sqrt[\textcolor{red}{m}]{\sqrt[\textcolor{blue}{n}]{a}}=\sqrt[\textcolor{red}{m}\textcolor{blue}{n}]{a}} \cdots④\)
以下に計算例を載せておきます。
例)
\(\underline{\bf{①の例}}\)
\(\begin{eqnarray}\sqrt[3]{2}×\sqrt[3]{4}&=&\sqrt[3]{2×4}\\\\&=&\sqrt[3]{2^3}\\\\&=&2\end{eqnarray}\)
\(\underline{\bf{②の例}}\)
\(\displaystyle{\frac{\sqrt[3]{12}}{\sqrt[3]{4}}=\sqrt[3]{\frac{12}{4}}=\sqrt[3]{3}}\)
\(\underline{\bf{③の例}}\)
\({(\sqrt[3]{5})}^{2}=\sqrt[3]{5^2}=\sqrt[3]{25}\)
\(\underline{\bf{④の例}}\)
\(\displaystyle{\sqrt[3]{\sqrt[4]{2}}=\sqrt[3×4]{2}=\sqrt[12]{2}}\)
3.有理数の指数
有理数の指数の意味は、次のようになっています。
\(a\gt0\)で、\(\textcolor{red}{m}\) , \(\textcolor{blue}{n}\)を正の整数、\(\textcolor{green}{r}\)を正の有理数とすると
\(\displaystyle{a^{\frac{1}{\textcolor{blue}{n}}}=\sqrt[\textcolor{blue}{n}]{a}} \cdots①\)
\(\displaystyle{a^{\frac{\textcolor{red}{m}}{\textcolor{blue}{n}}}={(\sqrt[\textcolor{blue}{n}]{a})}^{\textcolor{red}{m}}=\sqrt[\textcolor{blue}{n}]{a^{\textcolor{red}{m}}}} \cdots②\)
\(\displaystyle{a^{-\textcolor{green}{r}}=\frac{1}{a^{\textcolor{green}{r}}}} \cdots③\)
計算例を載せておきます。
例)
\(\underline{\bf{①の例}}\)
\(\displaystyle{2^{\frac{1}{3}}=\sqrt[3]{2}}\)
\(\underline{\bf{②の例}}\)
\(\displaystyle{2^{\frac{2}{3}}=\sqrt[3]{2^2}=\sqrt[3]{4}}\)
\(\underline{\bf{③の例}}\)
\(\displaystyle{3^{-\frac{1}{2}}=\frac{1}{\sqrt{3}}}\)
指数が有理数の場合にも、次の指数法則が成り立ちます。
\(a\gt0\) , \(b\gt0\)で、\(\textcolor{green}{r}\) , \(\textcolor{#ffd700}{s}\)を有理数とすると、
\(a^{\textcolor{green}{r}}×a^{\textcolor{#ffd700}{s}}=a^{\textcolor{green}{r}+\textcolor{#ffd700}{s}} \cdots④\)
\(\displaystyle{\frac{a^{\textcolor{green}{r}}}{a^{\textcolor{#ffd700}{s}}}=a^{\textcolor{green}{r}-\textcolor{#ffd700}{s}}} \cdots⑤\)
\({(a^{\textcolor{green}{r}})}^{\textcolor{#ffd700}{s}}=a^{\textcolor{green}{r}\textcolor{#ffd700}{s}} \cdots⑥\)
\({(ab)}^{\textcolor{green}{r}}=a^{\textcolor{green}{r}}b^{\textcolor{green}{r}} \cdots⑦\)
以下に計算例を載せておきます。
例)
\(\underline{\bf{④の例}}\)
\(\displaystyle{\begin{eqnarray}3^{\frac{2}{3}}×3^{\frac{4}{3}}&=&3^{\frac{2}{3}+\frac{4}{3}}\\\\&=&3^{\frac{6}{3}}\\\\&=&3^2\\\\&=&9\end{eqnarray}}\)
\(\underline{\bf{⑤の例}}\)
\(\displaystyle{\begin{eqnarray}\frac{5^{\frac{3}{4}}}{5^{\frac{1}{4}}}&=&5^{\frac{3}{4}-\frac{1}{4}}\\\\&=&5^{\frac{2}{4}}\\\\&=&5^{\frac{1}{2}}\\\\&=&\sqrt{5}\end{eqnarray}}\)
\(\underline{\bf{⑥の例}}\)
\(\begin{eqnarray}{(2^2)}^{3}&=&2^{2×3}\\\\&=&2^6\\\\&=&64\end{eqnarray}\)
\(\underline{\bf{⑦の例}}\)
\(\begin{eqnarray}{(3×2)}^{2}&=&3^2×2^2\\\\&=&9×4\\\\&=&36\end{eqnarray}\)
4.指数関数
\(a\)を\(1\)とは異なる正の実数とするとき、\(y=a^x\)は\(x\)の関数となります。
この関数を、\(\textcolor{red}{a}\)\(\textcolor{red}{\bf{を底とする}}\)\(\textcolor{red}{x}\)\(\textcolor{red}{\bf{の指数関数}}\)といいます。
一般に、\(y=a^x\)のグラフの概形は次のようになります。
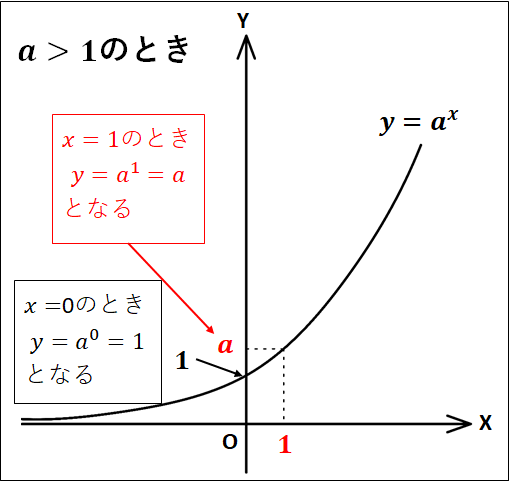
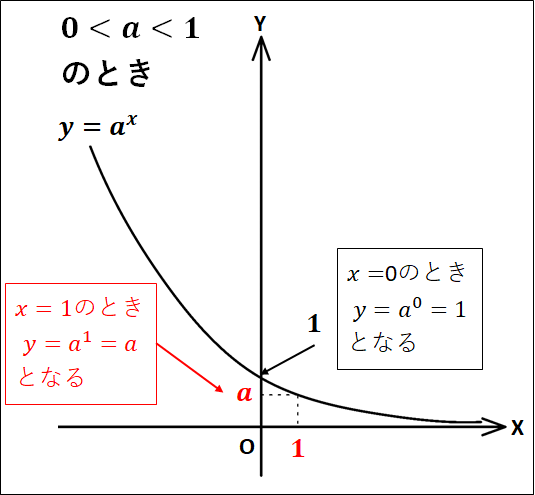
以下に、実際にどのような概形のグラフになるかの例を載せておきます。
(グラフの実際の数値と縮尺はずれていますが、概形は以下のようになります)
例)
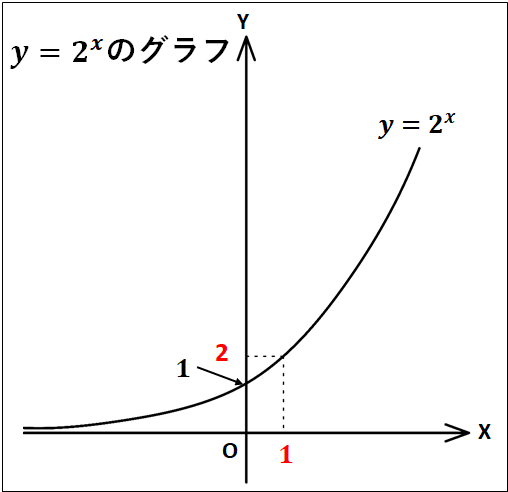
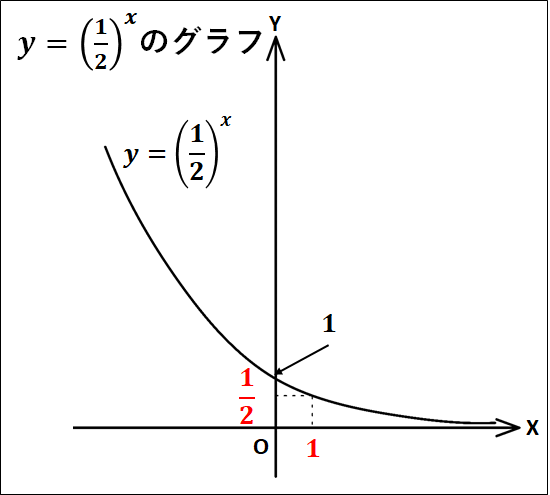
指数関数\(y=a^x\)の特徴は以下のようになります。
1. 定義域(\(x\)のとりうる値)は実数全体で、値域(\(y\)のとりうる値)は正の数全体。
2. \(a\gt0\)のとき、\(x\)の値が増加すると、\(y\)の値も増加する
\(r{\lt}s{\Leftrightarrow}a^r{\lt}a^s\)
3. \(0{\lt}a{\lt}1\)のとき、\(x\)の値が増加すると、\(y\)の値は減少する
\(r{\lt}s{\Leftrightarrow}a^r{\gt}a^s\)
\(x\)の値が増加すると、\(y\)の値も増加する関数を\(\textcolor{red}{\bf{増加関数}}\)といいます。
\(x\)の値が増加すると、\(y\)の値は減少する関数を\(\textcolor{blue}{\bf{減少関数}}\)といいます。
指数関数については、以上となります。
次回は、対数関数についての内容を予定していますので、よろしくお願いします。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


