【高校物理】極限【高校数学】【極限】

$\require{color}$

$\require{cancel}$

微分係数と導関数でも極限について少し扱いましたが、様々な関数の微分を考えるためには極限の考え方は必須となります。
ここでは、微分に関する公式を導くために必要な極限の考え方を解説しています。
基礎的な内容となるので、予習/復習をしたい方は是非、目を通してみてください。

微分・積分に関する記事は、こちらも参考にしてください

→微分係数と導関数

→積分法

→様々な関数

→微分法とその応用

→積分法の応用

→よく使う積分の考え方と微積公式まとめ

よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次

• 1.関数の極限とその性質
  • 1-1.極限
  • 1-2.極限の性質
  • 1-3.発散
  • 1-4.片側からの極限
  • 1-5.$x\to\infty,-\infty$の極限
• 2.いろいろな関数の極限
  • 2-1.指数関数の極限
  • 2-2.対数関数の極限
  • 2-3.三角関数の極限

1.関数の極限とその性質

1-1.極限

関数$f(x)$において、$x$が$\textcolor{blue}{a}$とは異なる値をとりながら$\textcolor{blue}{a}$に限りなく近づくとき、$f(x)$の値が一定の値$\textcolor{red}{\alpha}$に限りなく近づくならば、この値$\textcolor{red}{\alpha}$を$x→\textcolor{blue}{a}$のときの$f(x)$の極限値といい、$\displaystyle{\lim_{x\to{\textcolor{blue}{a}}}f(x)=\textcolor{red}{\alpha}}$または、$x→\textcolor{blue}{a}$のとき$f(x)→\textcolor{red}{\alpha}$と書き表します。

例)

$f(x)=x^2-x$において、$x$の値を限りなく$2$に近づけるとき、


$\displaystyle{\begin{eqnarray}\lim_{x\to2}f(x)&=&\lim_{x\to2}(x^2-x)\\\\&=&2\end{eqnarray}}$


となります。
グラフの概形は以下のようになります。

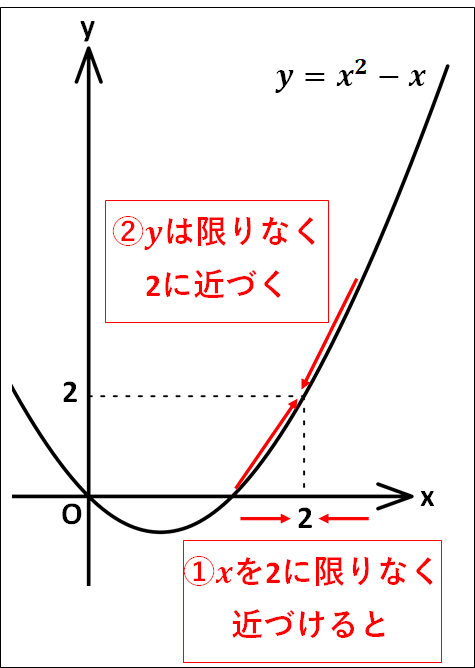
※計算としては$f(x)=x^2-x$に$x=2$を代入したものとなりますが、あくまでも$x$は$2$ではなく、$+2.000\cdots1$や$+1.9999\cdots$など限りなく$2$に近づけるという意味になります。またその際、$f(x)$は値$2$になるのではなく、$2$に限りなく近づくという意味になります。

→目次へ戻る

1-2.極限の性質

極限の性質には下記のようなものがあります。

$\displaystyle{\lim_{x\to{a}}f(x)=\textcolor{red}{\alpha}}$、$\displaystyle{\lim_{x\to{a}}g(x)=\textcolor{blue}{\beta}}$とすると、




$\displaystyle{\lim_{x\to{a}}kf(x)=k\textcolor{red}{\alpha}　(kは定数) \cdots①}$


$\displaystyle{\lim_{x\to{a}}{f(x)+g(x)}=\textcolor{red}{\alpha}+\textcolor{blue}{\beta} \cdots②}$


$\displaystyle{\lim_{x\to{a}}{f(x)-g(x)}=\textcolor{red}{\alpha}-\textcolor{blue}{\beta} \cdots③}$


$\displaystyle{\lim_{x\to{a}}f(x)g(x)=\textcolor{red}{\alpha}\textcolor{blue}{\beta} \cdots④}$


$\displaystyle{\lim_{x\to{a}}\frac{f(x)}{g(x)}=\frac{\textcolor{red}{\alpha}}{\textcolor{blue}{\beta}}　(ただし\textcolor{blue}{\beta}\neq0) \cdots⑤}$



上記性質は、普通の計算の際に行うものと似ているので、覚えやすいと思います。
下記に計算例を載せておきます。

$f(x)=2x+3$、$g(x)=x+1$とすると、

$\displaystyle{\begin{eqnarray}\lim_{x\to1}f(x)&=&\lim_{x\to1}(2x+3)\\&=&5\end{eqnarray}}$


$\displaystyle{\begin{eqnarray}\lim_{x\to1}g(x)&=&\lim_{x\to1}(x+1)\\&=&2\end{eqnarray}}$


となります。

これをもとにして、計算例をみていきます。



$\underline{\bf{①の計算例}}$

$\displaystyle{\begin{eqnarray}\lim_{x\to1}3f(x)&=&3\lim_{x\to1}f(x)\\\\&=&3×5\\\\&=&15\end{eqnarray}}$



$\underline{\bf{②の計算例}}$

$\displaystyle{\begin{eqnarray}\lim_{x\to1}\{f(x)+g(x)\}&=&(5+2)\\\\&=&7\end{eqnarray}}$



$\underline{\bf{③の計算例}}$

$\displaystyle{\begin{eqnarray}\lim_{x\to1}\{f(x)-g(x)\}&=&(5-2)\\\\&=&3\end{eqnarray}}$



$\underline{\bf{④の計算例}}$

$\displaystyle{\begin{eqnarray}\lim_{x\to1}\{f(x)g(x)\}&=&5×2\\\\&=&10\end{eqnarray}}$



$\underline{\bf{⑤の計算例}}$

$\displaystyle{\begin{eqnarray}\lim_{x\to1}\frac{f(x)}{g(x)}&=&\frac{5}{2}\end{eqnarray}}$

また、上の計算例をみてみると

$\displaystyle{\lim_{x\to{a}}f(x)=f(a)}$

となっています。



例えば、1-1.極限の例を見てみると、

$f(x)=x^2-x$のとき


$\displaystyle{\begin{eqnarray}\lim_{x\to2}f(x)&=&f(2)\\\\&=&(2^2-2)\\\\&=&2\end{eqnarray}}$


となっています。

一般に、$x$の多項式で表される関数や分数関数、無理関数、三角関数、指数関数、対数関数などについては、$a$が関数$f(x)$の定義域の値であれば、


$\displaystyle{\lim_{x\to{a}}f(x)=f(a)}$


が成り立ちます。

→目次へ戻る

1-3.発散

関数$f(x)$において、$x$が$a$と異なる値をとりながら$a$に限りなく近づくとき、$f(x)$の値が限りなく大きくなるならば、

$x\to{a}$のとき$f(x)$は正の無限大に発散する

または

$x\to{a}$のとき$f(x)$の極限は$\infty$である


といい、


$\displaystyle{\lim_{x\to{a}}f(x)=\infty}$

または、

$x\to{a}$のとき$f(x)\to{\infty}$


と書き表します。

また、$x$が$a$と異なる値をとりながら$a$に限りなく近づくとき、$f(x)$の値が負で、その絶対値が限りなく大きくなるならば、

$x\to{a}$のとき$f(x)$は負の無限大に発散する

または、

$x\to{a}$のとき$f(x)$の極限は$-\infty$である


といい


$\displaystyle{\lim_{x\to{a}}f(x)=-\infty}$

または、

$x\to{a}$のとき$f(x)\to-\infty$


と書き表します。

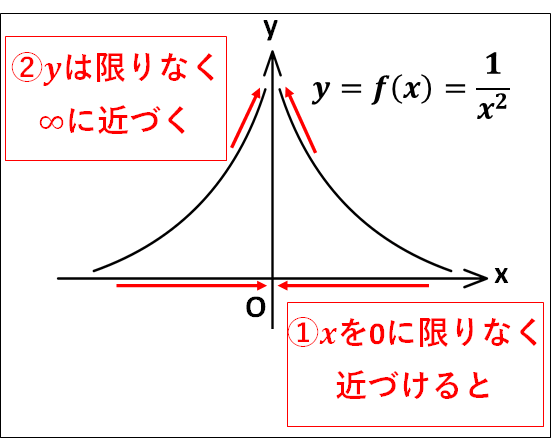
例)

$\displaystyle{\lim_{x\to0}\frac{1}{x^2}=\infty}$

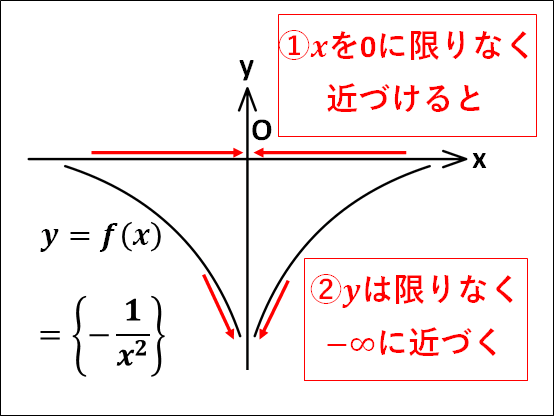
$\displaystyle{\lim_{x\to0}{-\frac{1}{x^2}}=-\infty}$

→目次へ戻る

1-4.片側からの極限

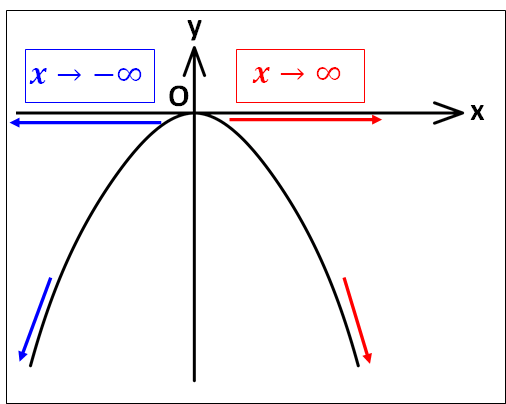
$\displaystyle{f(x)=\frac{2x^2+x}{|x|}}$を考えてみます。

$x\gt0$のとき、


$\displaystyle{f(x)=\frac{2x^2+x}{x}=2x+1}$

$x\lt0$のとき


$\displaystyle{f(x)=\frac{2x^2+x}{-x}=-2x-1}$



ここで、$x\to0$を考えたとき、下図のようになります。

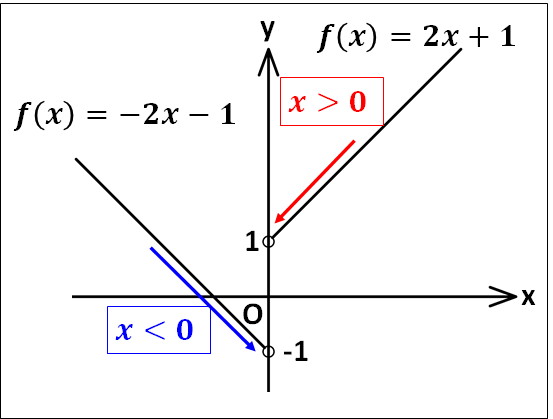
上図から、$x\gt0$の範囲で$x$が$0$に限りなく近づくとき、$f(x)$の値は$1$に限りなく近づきます。
また、$x\lt0$の範囲で$x$が$0$に限りなく近づくとき、$f(x)$の値は$-1$に限りなく近づきます。


このことから、$x$を同じ値に近づけても近づける方向によって極限値が変わることが分かります。

一般に、


$x\gt{a}$の範囲で$x$が$a$に限りなく近づくとき、$f(x)$が一定の値$\textcolor{red}{\alpha}$に限りなく近づくならば、$\textcolor{red}{\alpha}$を$x$が$a$に近づくときの$f(x)$の$\textcolor{red}{\bf{右側極限}}$といい

$\displaystyle{\lim_{x\to{a+0}}f(x)=\textcolor{red}{\alpha}}$

と書き表します。


$x\lt{a}$の範囲で$x$が$a$に限りなく近づくときの$\textcolor{blue}{\bf{左側極限}}$も同様に定義でき、その極限値が$\textcolor{blue}{\beta}$のとき、

$\displaystyle{\lim_{x\to{a-0}}f(x)=\textcolor{blue}{\beta}}$

と書き表します。

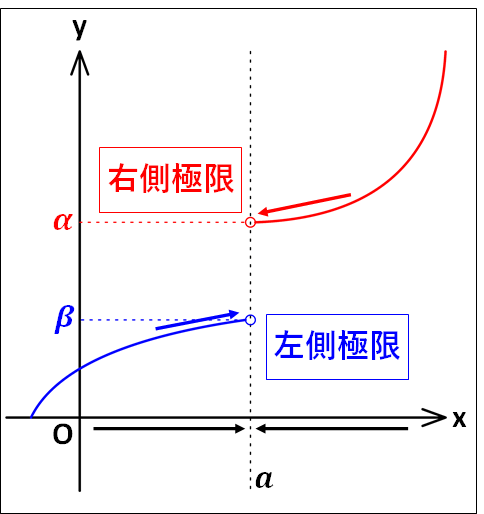
$a=0$のときは、$(x\to{a+0})$、$(x\to{a-0})$をそれぞれ$(x\to{+0})$、$(x\to{-0})$と書きます。

右側極限と左側極限に関して、関数$f(x)$において次のことが成り立ちます。


$\displaystyle{\begin{eqnarray}&&\lim_{x\to{a+0}}f(x)=\lim_{x\to{a-0}}f(x)=\alpha\\\\\Leftrightarrow&&\lim_{x\to{a}}f(x)=\alpha\end{eqnarray}}$


上式は、$x$を$a$に限りなく近づけた右側極限と左側極限がおなじ値$\alpha$なら、$x\to{a}$のときの$f(x)$の極限が$\alpha$であることを表しています。


もしも、$\displaystyle{\lim_{x\to{a+0}}f(x)}$と$\displaystyle{\lim_{x\to{a-0}}f(x)}$が存在しても、それらの値が一致しないとき、$x\to{a}$のときの$f(x)$の極限はないということになります。



例えば、前例の$\displaystyle{f(x)=\frac{2x^2+x}{|x|}}$において、


$\displaystyle{\lim_{x\to{+0}}f(x)=1}$

$\displaystyle{\lim_{x\to{-0}}f(x)=-1}$


なので、右側極限と左側極限は一致しておらず、$x\to0$のときの$f(x)$の極限はないということになります。

また、右側極限、左側極限が$\infty$または$-\infty$になるとき、

$\displaystyle{\lim_{x\to{a+0}}f(x)=\infty}$

$\displaystyle{\lim_{x\to{a-0}}f(x)=-\infty}$

のように書き表します。

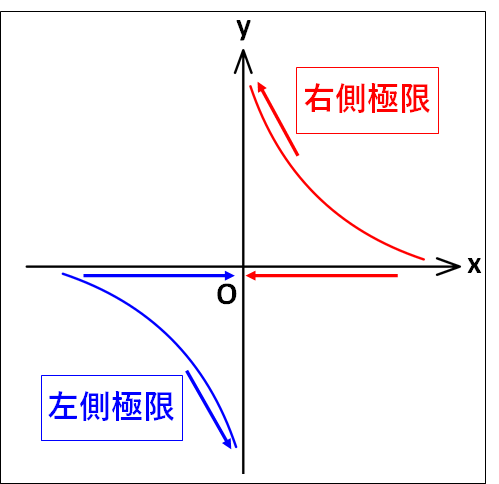
例)　$\displaystyle{f(x)=\frac{1}{x}}$について


$\displaystyle{\lim_{x\to+0}\frac{1}{x}=\infty}$

$\displaystyle{\lim_{x\to-0}\frac{1}{x}=-\infty}$

となります。

→目次へ戻る

1-5.$x\to\infty,-\infty$の極限

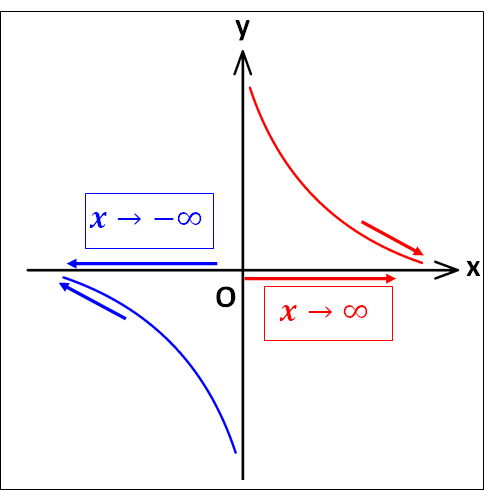
$x\to\infty$のとき$f(x)$の値が一定の値$\textcolor{red}{\alpha}$に限りなく近づくならば、この値$\textcolor{red}{\alpha}$を$x\to\infty$のときの$f(x)$の極限値または、極限といい$\displaystyle{\lim_{x\to\infty}f(x)=\textcolor{red}{\alpha}}$と書き表します。

$x\to-\infty$の場合も同様に考えて、$\displaystyle{\lim_{x\to-\infty}f(x)=\textcolor{red}{\alpha}}$と書き表します。

例)　$\displaystyle{f(x)=\frac{1}{x}}$のとき


$\displaystyle{\lim_{x\to\infty}f(x)=\lim_{x\to\infty}\frac{1}{x}=0}$

$\displaystyle{\lim_{x\to-\infty}f(x)=\lim_{x\to-\infty}\frac{1}{x}=0}$

となります。

$x\to\infty$や$x\to-\infty$のときに、関数$f(x)$の極限が$\infty$または$-\infty$になる場合も$x\to{a}$のときと同様に考えます。

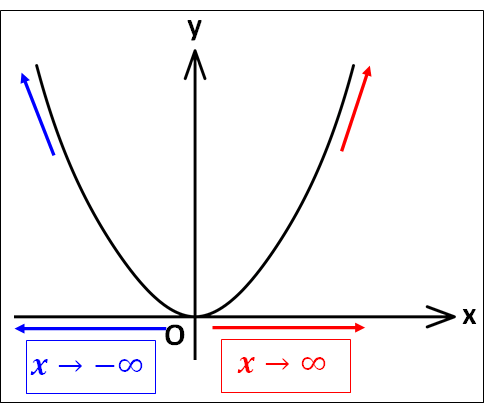
例1)　$f(x)=x^2$のとき


$\displaystyle{\lim_{x\to\infty}f(x)=\lim_{x\to\infty}x^2=\infty}$

$\displaystyle{\lim_{x\to-\infty}f(x)=\lim_{x\to-\infty}x^2=\infty}$

となります。

例2)　$f(x)=-x^2$のとき


$\displaystyle{\lim_{x\to\infty}f(x)=\lim_{x\to\infty}(-x^2)=-\infty}$

$\displaystyle{\lim_{x\to-\infty}f(x)=\lim_{x\to-\infty}(-x^2)=-\infty}$

となります。

→目次へ戻る

2.いろいろな関数の極限

2-1.指数関数の極限

$\underline{\bf{指数関数の極限}}$

指数関数についてはこちらも参考にしてください
→指数関数


指数関数の極限については、以下のようになります。

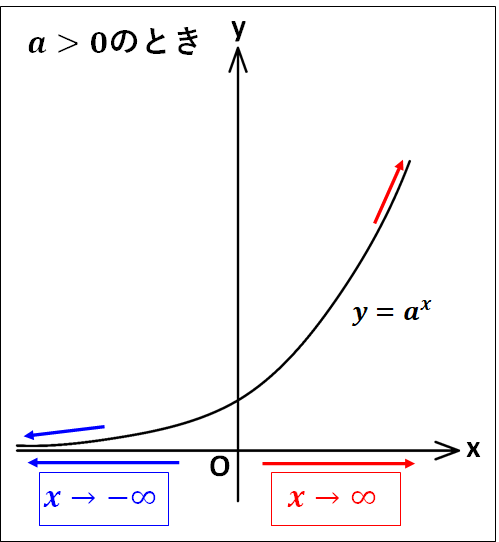
指数関数$y=a^x$について


○$a\gt0$のとき

$\displaystyle{\textcolor{red}{\lim_{x\to\infty}a^x=\infty}}$

$\displaystyle{\textcolor{blue}{\lim_{x\to-\infty}a^x=0}}$

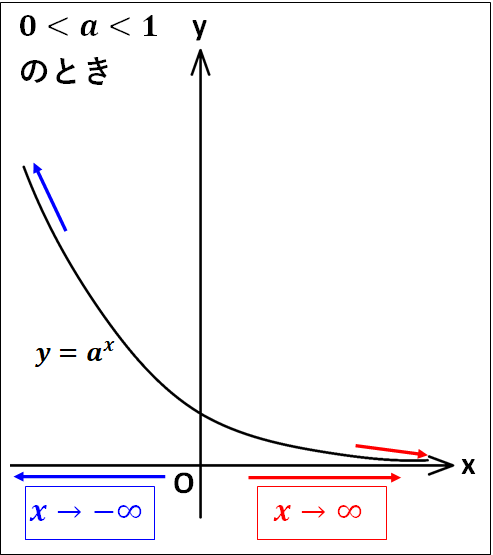
○$0\lt{a}\lt1$のとき

$\displaystyle{\textcolor{red}{\lim_{x\to\infty}a^x=0}}$

$\displaystyle{\textcolor{blue}{\lim_{x\to-\infty}a^x=\infty}}$

→目次へ戻る

2-2.対数関数の極限

対数関数についてはこちらも参考にしてください
→対数関数


対数関数の極限については、以下のようになります。

対数関数$y=\log_a{x}$について


○$a\gt0$のとき

$\displaystyle{\textcolor{red}{\lim_{x\to\infty}\log_a{x}=\infty}}$

$\displaystyle{\textcolor{blue}{\lim_{x\to{+0}}\log_a{x}=-\infty}}$

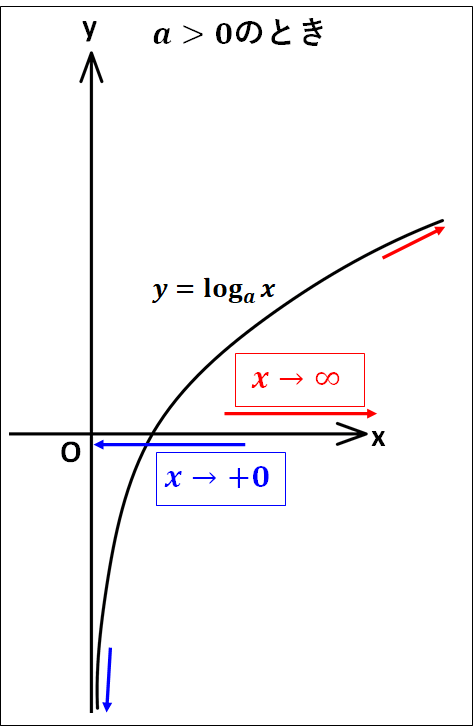
○$0\lt{a}\lt1$のとき

$\displaystyle{\textcolor{red}{\lim_{x\to\infty}\log_a{x}=-\infty}}$

$\displaystyle{\textcolor{blue}{\lim_{x\to+0}\log_a{x}=\infty}}$

→目次へ戻る

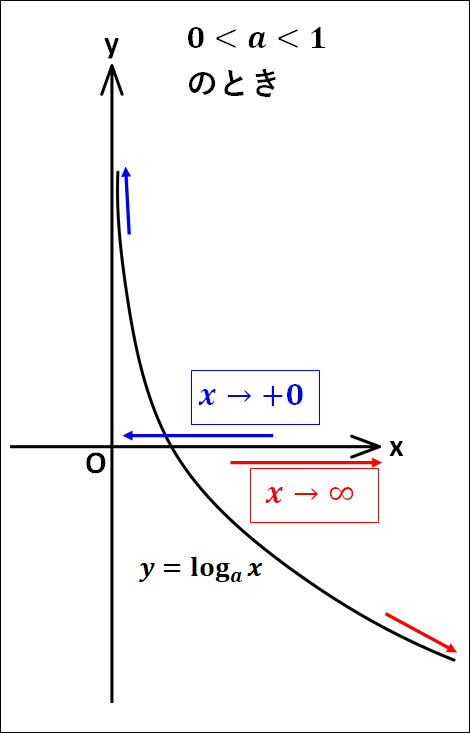
2-3.三角関数の極限

三角関数のグラフについてはこちらも参考にしてください
→三角関数の定義と関係式
→三角関数のグラフ


三角関数の解説では、変数$\theta$を用いましたが、ここでは変数$\theta$の代わりに変数$x$を用います。
変数が$x$になっても、扱い方自体は変わりません。

$\underline{{\sin{x}}{\bf{と}}{\cos{x}}{\bf{の極限}}}$

$\sin{x}$と$\cos{x}$についてですが、これらは周期関数であり変数$x$の変化とともに$-1$と$1$の間の値を繰り返します。
よって、$x\to\infty$としても一定の値に近づかないので、$x\to\infty$のとき、$\sin{x}$と$\cos{x}$の極限はありません。

$\underline{{\tan{x}}{\bf{の極限}}}$

$\tan{x}$については、

$\displaystyle{\lim_{x\to\frac{\pi}{2}+0}\tan{x}=-\infty}$

$\displaystyle{\lim_{x\to\frac{\pi}{2}-0}\tan{x}=\infty}$

となります。

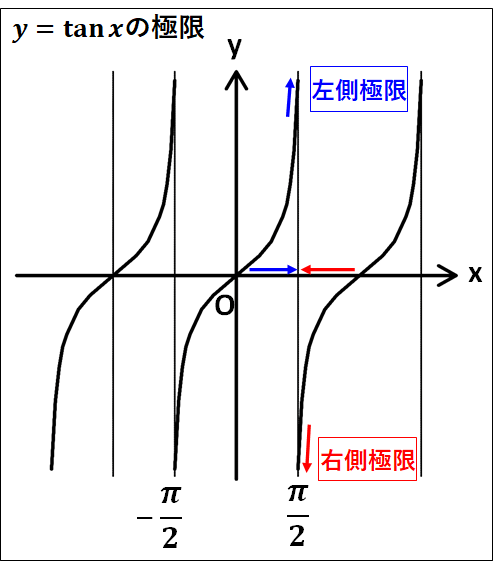
しかしながら、


$\displaystyle{\lim_{x\to\frac{\pi}{2}+0}\tan{x}\neq\lim_{x\to\frac{\pi}{2}-0}\tan{x}}$


なので、$\displaystyle{x\to\frac{\pi}{2}}$のときの$\tan{x}$の極限はありません。

$\underline{\bf{関数の極限の性質}}$

関数の極限には次の性質があります。



$\displaystyle{\lim_{x\to{a}}f(x)=\textcolor{red}{\alpha}}$、$\displaystyle{\lim_{x\to{a}}g(x)=\textcolor{blue}{\beta}}$とすると


$\bf{性質1)}$　$x=a$の近くで常に$f(x)\le{g(x)}$ならば、

$\displaystyle{\lim_{x\to{a}}f(x)\le{\lim_{x\to{a}}g(x)}}$

すなわち、

$\textcolor{red}{\alpha}\le\textcolor{blue}{\beta}$

が成り立つ。


$\bf{性質2)}$　$x=a$の近くで常に$f(x)\le{h(x)}\le{g(x)}$かつ$\textcolor{red}{\alpha}=\textcolor{blue}{\beta}$ならば、

$\displaystyle{\lim_{x\to{a}}h(x)=\textcolor{red}{\alpha}}$

が成り立つ。

この性質を”はさみうちの原理”ということもあります。



次に、この性質2)を用いて、$\displaystyle{\frac{\sin{x}}{x}}$の極限を求めてみます。

$\displaystyle{\underline{{\frac{\sin{x}}{x}}\bf{の極限}}}$


$\displaystyle{\lim_{x\to0}\frac{\sin{x}}{x}}$について、


$\displaystyle{0\lt{x}\lt\frac{\pi}{2}}$のとき、下図を考えます。

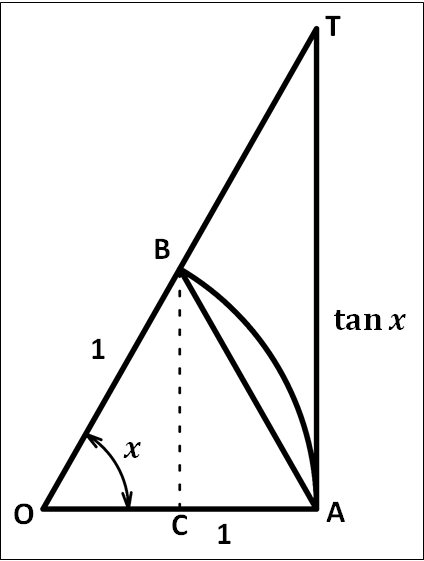
上図は、単位円において三角形を切り取った形をしています。

単位円で考えているので、

$\begin{eqnarray}OA&=&OB\\\\&=&{\bf{(半径)}}\\\\&=&1\end{eqnarray}$


また、

$\displaystyle{\begin{eqnarray}&&\tan{x}=\frac{AT}{OA}\\\\\Leftrightarrow&&AT=OA×\tan{x}\\\\\Leftrightarrow&&AT=1×\tan{x}\\\\\Leftrightarrow&&AT=\tan{x}\end{eqnarray}}$

となります。


図から、$△OAB$、${\bf{扇形}}OAB$、$△OAT$の面積の大きさを比較すると

$△OAB\lt{\bf{扇形}}OAB\lt△OAT　\cdots①$

となります。

それぞれの面積については、



$\underline{△OAB}$

${\bf{底辺}}=OA=1$

${\bf{高さ}}=BC=1×\sin{x}=\sin{x}$

よって、

$\displaystyle{\begin{eqnarray}△OAB&=&{\bf{底辺}}×{\bf{高さ}}×\frac{1}{2}\\\\&=&1×\sin{x}×\frac{1}{2}\\\\&=&\frac{1}{2}\sin{x}\end{eqnarray}}$




$\underline{{\bf{扇形}}OAB}$

扇形の面積は、

$\displaystyle{{\bf{(円の面積)}}×\frac{{\bf{扇形の角度}}}{{\bf{円の角度}}}}$

となります。


$\begin{eqnarray}{\bf{円の面積}}&=&{\bf{(半径)}}{^2}×\pi\\\\&=&1^2×\pi\\\\&=&\pi\end{eqnarray}$

${\bf{扇形の角度}}=x$

${\bf{円の角度}}=2\pi$


よって、

$\displaystyle{\begin{eqnarray}{\bf{扇形}}OAB&=&{\bf{(円の面積)}}×\frac{{\bf{扇形の角度}}}{{\bf{円の角度}}}\\\\&=&\pi×\frac{x}{2\pi}\\\\&=&\frac{1}{2}x\end{eqnarray}}$




$\underline{△OAT}$

${\bf{底辺}}=OA=1$

${\bf{高さ}}=AT=\tan{x}$

よって、

$\displaystyle{\begin{eqnarray}△OAT&=&{\bf{底辺}}×{\bf{高さ}}×\frac{1}{2}\\\\&=&1×\tan{x}×\frac{1}{2}\\\\&=&\frac{1}{2}\tan{x}\end{eqnarray}}$




これらを、$①$に代入すると、

$\displaystyle{\begin{eqnarray}&&△OAB\lt{\bf{扇形}}OAB\lt△OAT\\\\\Leftrightarrow&&\frac{1}{2}\sin{x}\lt\frac{1}{2}x\lt\frac{1}{2}\tan{x}\end{eqnarray}}$



$\displaystyle{0\lt{x}\lt\frac{\pi}{2}}$のとき$\sin{x}\gt0$なので、各辺$\displaystyle{\frac{2}{\sin{x}}}$を掛けて


$\displaystyle{\begin{eqnarray}&&\frac{1}{2}\sin{x}\lt\frac{1}{2}x\lt\frac{1}{2}\tan{x}\\\\\Leftrightarrow&&\frac{2\sin{x}}{2\sin{x}}\lt\frac{2x}{2\sin{x}}\lt\frac{2\tan{x}}{2\sin{x}}\\\\\Leftrightarrow&&1\lt\frac{x}{\sin{x}}\lt\frac{\tan{x}}{\sin{x}}\end{eqnarray}}$



ここで、$\displaystyle{\tan{x}=\frac{\sin{x}}{\cos{x}}}$なので、



$\displaystyle{\begin{eqnarray}\frac{\tan{x}}{\sin{x}}&=&\frac{\sin{x}}{\cos{x}×\sin{x}}\\\\&=&\frac{1}{\cos{x}}\end{eqnarray}}$



よって、

$\displaystyle{\begin{eqnarray}&&1\lt\frac{x}{\sin{x}}\lt\frac{\tan{x}}{\sin{x}}\\\\\Leftrightarrow&&1\lt\frac{x}{\sin{x}}\lt\frac{1}{\cos{x}}\end{eqnarray}}$



上記不等式の逆数をとって、

$\displaystyle{\cos{x}\lt\frac{\sin{x}}{x}\lt1}　\cdots②$



いま、$\displaystyle{0\lt{x}\lt\frac{\pi}{2}}$より$x\gt0$なので、$\cos{x}$に関して$x\to+0$とすると、

$\displaystyle{\lim_{x\to+0}\cos{x}=1}$

となります。



これと性質2)の”はさみうちの原理”から、

$\displaystyle{\lim_{x\to+0}\frac{\sin{x}}{x}=1}$

となります。

次に、$\displaystyle{-\frac{\pi}{2}\lt{x}\lt0}$のとき、辺々に$-1$を掛けて、


$\displaystyle{0\lt-x\lt\frac{\pi}{2}}$


となります。


また、

$\cos(-x)=\cos{x}$

$\sin(-x)=-\sin{x}$

なので、$②$から、


$\displaystyle{\begin{eqnarray}&&\cos(-x)\lt\frac{\sin(-)}{-x}\lt1\\\\\Leftrightarrow&&\cos{x}\lt\frac{\sin{x}}{x}\lt1\end{eqnarray}}$


いま、$\displaystyle{-\frac{\pi}{2}\lt{x}\lt0}$より$x\lt0$なので、$\cos{x}$に関して$x\to-0$とすると、


$\displaystyle{\lim_{x\to-0}\cos{x}=1}$


となり、これと性質2)の”はさみうちの原理”から、


$\displaystyle{\lim_{x\to-0}\frac{\sin{x}}{x}=1}$

以上から、

$\displaystyle{\lim_{x\to+0}\frac{\sin{x}}{x}=\lim_{x\to-0}\frac{\sin{x}}{x}=1}$

となり、右側極限と左側極限が同じ値となるので、$x\to0$としたとき$\displaystyle{\frac{\sin{x}}{x}}$は極限値をもち


$\displaystyle{\lim_{x\to0}\frac{\sin{x}}{x}=1}$


となります。




今回は以上となります。

よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

→目次へ戻る


→高校物理へ戻る


→ホームへ戻る

関連記事
→微分係数と導関数

→積分法

→様々な関数

→微分法とその応用

→積分法の応用

→よく使う積分の考え方と微積公式まとめ