【高校物理】ベクトル②/内積と外積【高校数学】【ベクトル】

$\require{color}$

$\require{cancel}$

今回は、ベクトルの内積と外積について説明していきます。
物理において、内積は仕事の定義となり、外積は電磁気分野のローレンツ力の計算などに用います。
外積自体は、高校数学で用いることはないと思いますがこの機会にかじっておきましょう。

ベクトルに関する記事は、こちらも参考にしてください。

→ベクトルの演算と成分表示

→練習問題(内積/外積など)

よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次

• 1.内積
  • 1-1.内積の定義
  • 1-2.内積の成分表示
  • 1-3.内積の性質
• 2.外積

1.内積

1-1.内積の定義

下図のように点$O , A , B$をとり、$\textcolor{red}{\vec{a}=\overrightarrow{OA}}$ , $\textcolor{blue}{\vec{b}=\overrightarrow{OB}}$とします。

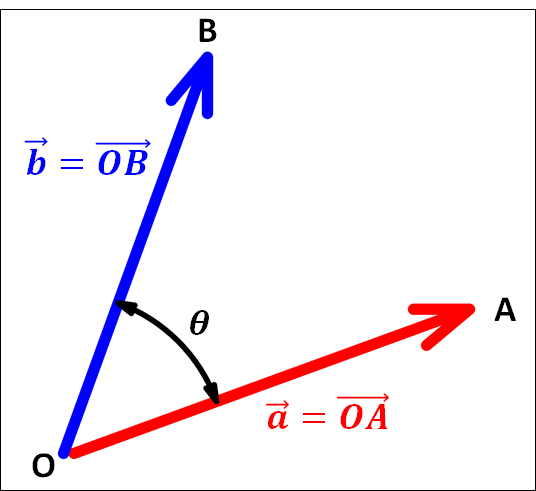
$OA$と$OB$でつくられる角度のうち、$0^{\circ}\le\theta\le180^{\circ}$であるものを、$\textcolor{red}{\vec{a}}$,$\textcolor{blue}{\vec{b}}$のなす角といいます。
$\textcolor{red}{\vec{a}}{\neq}\vec{0}$、$\textcolor{blue}{\vec{b}}{\neq}\vec{0}$、なす角を$\theta$とすると下式の積

$\textcolor{red}{|\vec{a}|}\textcolor{blue}{|\vec{b}|}\cos\theta$

を$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$の内積といい、記号$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}$で表します。
内積は、上記式のように

$(\textcolor{red}{{\vec{a}}\bf{の大きさ}})×(\textcolor{blue}{{\vec{b}}\bf{の大きさ}})×(\bf{なす角}\cos\theta)$

となります。
ここで、それぞれのベクトルの大きさはベクトルではなくスカラー(向きを持たず大きさだけをもつ)です。
また、なす角$\cos\theta$もスカラーとなるので、$\textcolor{red}{\bf{ベクトルの内積はベクトルではなくスカラー}}$となります。

次に、例として角度によって内積がどのようになるのかをみていきます。
$\cos\theta$の特徴的な値はそれぞれ

$\cos0^{\circ}=1$

$\cos180^{\circ}=-1$

$\cos90^{\circ}=0$

です。

ここで内積を考えます。
$\textcolor{red}{\vec{a}}\neq\vec{0}$ , $\textcolor{blue}{\vec{b}}\neq\vec{0}$ , なす角を$\theta　(0^{\circ}\le\theta\le180^{\circ})$とすると



$\theta=0^{\circ}$($\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$が同じ向きに平行)のとき

$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{\vec{|a|}}\textcolor{blue}{\vec{|b|}}×1=\textcolor{red}{\vec{|a|}}\textcolor{blue}{\vec{|b|}}$




$\theta=180^{\circ}$($\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$が反対の向きに平行)のとき

$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{\vec{|a|}}\textcolor{blue}{\vec{|b|}}×(-1)=-\textcolor{red}{\vec{|a|}}\textcolor{blue}{\vec{|b|}}$




$\theta=90^{\circ}$($\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$が垂直)のとき

$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{\vec{|a|}}\textcolor{blue}{\vec{|b|}}×0=0$


となります。

ここで、$\theta=90^{\circ}$のときについて$\textcolor{red}{\vec{|a|}}{\neq}0$、$\textcolor{blue}{\vec{|b|}}{\neq}0$で$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=0$ならば、$\cos\theta$が$0$ということになり、このとき$\theta=90^{\circ}$なので$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$は垂直であることが分かります。

→目次へ戻る

1-2.内積の成分表示

三角形$OAB$を考え、$\textcolor{red}{\overrightarrow{OA}=\vec{a}}$ , $\textcolor{blue}{\overrightarrow{OB}=\vec{b}}$とすると

$\textcolor{green}{\overrightarrow{AB}}=\textcolor{blue}{\vec{b}}-\textcolor{red}{\vec{a}}$

となります。

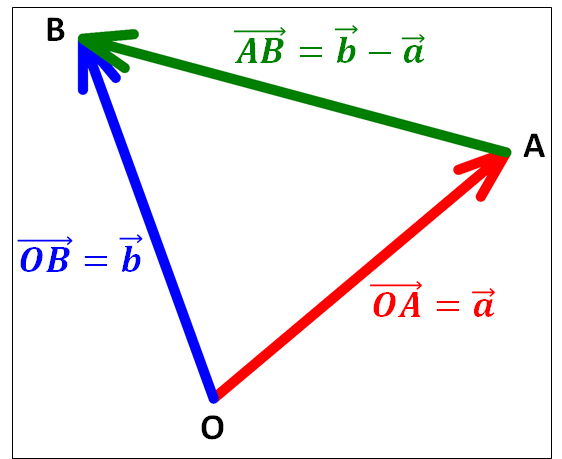
ここで、三角形$OAB$に余弦定理を用いて

$\textcolor{green}{BA^2}=\textcolor{red}{OA^2}+\textcolor{blue}{OB^2}-2×\textcolor{red}{OA}×\textcolor{blue}{OB}\cos\theta$

これをベクトルで表すと、

$|\textcolor{red}{\vec{a}}-\textcolor{blue}{\vec{b}}|^2=|\textcolor{red}{\vec{a}}|^2+|\textcolor{blue}{\vec{b}}|^2-2(\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}})$

ここで、$\textcolor{red}{\vec{a}=(a_{1},a_{2})}$、$\textcolor{blue}{\vec{b}=(b_{1},b_{2})}$とすると上式は、



$\begin{eqnarray}&&(\textcolor{red}{a_{1}}-\textcolor{blue}{b_{1}})^2+(\textcolor{red}{a_{2}}-\textcolor{blue}{b_{2}})^2\\=&&({\textcolor{red}{a_{1}}}^2+{\textcolor{red}{a_{2}}}^2)+({\textcolor{blue}{b_{1}}}^2+{\textcolor{blue}{b_{2}}}^2)-2(\textcolor{red}{\vec{a}}・\textcolor{red}{\vec{b}})\end{eqnarray}$



これを式変形して整理すると、

$\begin{eqnarray}&&-2{\textcolor{red}{a_{1}}}{\textcolor{blue}{b_{1}}}-2{\textcolor{red}{a_{2}}}{\textcolor{blue}{b_{2}}}=-2(\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}})\\\Leftrightarrow&&\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{a_{1}}\textcolor{blue}{b_{1}}+\textcolor{red}{a_{2}}\textcolor{blue}{b_{2}}\end{eqnarray}$

となります。

以上から、

$\textcolor{red}{\underline{\textcolor{black}{\bf{ベクトルの内積の成分表示は}}}}$

$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{a_{1}}\textcolor{blue}{b_{1}}+\textcolor{red}{a_{2}}\textcolor{blue}{b_{2}}$

となります。

次にベクトルのなす角について、$\textcolor{red}{\vec{a}}\neq\vec{0}$ , $\textcolor{blue}{\vec{b}}\neq\vec{0}$のとき内積の定義から

$\displaystyle{\begin{eqnarray}&&\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=|\textcolor{red}{\vec{a}}||\textcolor{blue}{\vec{b}}|\cos\theta\\\\\Leftrightarrow&&\cos\theta=\frac{\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}}{|\textcolor{red}{\vec{a}}||\textcolor{blue}{\vec{b}}|}\end{eqnarray}}$

となります。
また、$\textcolor{red}{\vec{a}}=(\textcolor{red}{a_{1}},\textcolor{red}{a_{2}})$ , $\textcolor{blue}{\vec{b}}=(\textcolor{blue}{b_{1}},\textcolor{blue}{b_{2}})$のとき、

$|\textcolor{red}{\vec{a}}|=\sqrt{{\textcolor{red}{a_{1}}}^2+{\textcolor{red}{a_{2}}}^2}$

$|\textcolor{blue}{\vec{b}}|=\sqrt{{\textcolor{blue}{b_{1}}}^2+{\textcolor{blue}{b_{2}}}^2}$

$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{a_{1}}\textcolor{blue}{b_{1}}+\textcolor{red}{a_{2}}\textcolor{blue}{b_{2}}$

これらを内積の定義式に代入して、

$\displaystyle{\cos\theta=\frac{\textcolor{red}{a_{1}}\textcolor{blue}{b_{1}}+\textcolor{red}{a_{2}}\textcolor{blue}{b_{2}}}{\sqrt{{\textcolor{red}{a_{1}}}^2+{\textcolor{red}{a_{2}}}^2}\sqrt{{\textcolor{blue}{b_{1}}}^2+{\textcolor{blue}{b_{2}}}^2}}}$

となります。



成分表示における垂直条件については、
$\textcolor{red}{\vec{a}}\neq\vec{0}$ , $\textcolor{blue}{\vec{b}}\neq\vec{0}$のとき

$\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=0$ならば$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$は垂直であったので、成分表示でも同様に

$\textcolor{red}{a_{1}}\textcolor{blue}{b_{1}}+\textcolor{red}{a_{2}}\textcolor{blue}{b_{2}}=0$

であれば、$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$は垂直となります。

→目次へ戻る

1-3.内積の性質

内積の性質は以下のようになります。


$\vec{a}・\vec{a}=|\vec{a}|^2 \cdots①$

$\vec{a}・\vec{b}=\vec{b}・\vec{a} \cdots②$

$(\vec{a}+\vec{b})・\vec{c}=\vec{a}・\vec{c}+\vec{b}・\vec{c} \cdots③$

$\vec{a}・(\vec{b}+\vec{c})=\vec{a}・\vec{b}+\vec{a}・\vec{c} \cdots④$

$(k\vec{a})・\vec{b}=\vec{a}・(k\vec{b})=k(\vec{a}・\vec{b}) \cdots⑤$

$\underline{\bf{①について}}$

$\vec{a}=(a_{1},a_{2})$とすると、

$\begin{eqnarray}\vec{a}・\vec{a}&=&{a_{1}}^2+{a_{2}}^2\\\\&=&(\sqrt{{a_{1}}^2+{a_{2}}^2})^2\\\\&=&|\vec{a}|^2\end{eqnarray}$

となります。

$\underline{\bf{②について}}$

内積の定義式$\vec{a}・\vec{b}=|\vec{a}||\vec{b}|\cos\theta$の形から、$\vec{a}$と$\vec{b}$のなす角は変わらずに、$|\vec{a}|$と$|\vec{b}|$は実数なので(向きをもたないのでベクトルでない)掛ける順番を入れ替えても同じとなる。
よって、

$\begin{eqnarray}\vec{a}・\vec{b}&=&|\vec{a}||\vec{b}|\cos\theta\\\\&=&|\vec{b}||\vec{a}|\cos\theta\\\\&=&\vec{b}・\vec{a}\end{eqnarray}$

となります。

$\underline{\bf{③について}}$

$③$の左辺を成分表示で考えて式変形をしていきます。

$\begin{eqnarray}(\vec{a}+\vec{b})・\vec{c}&=&(a_{1}+b_{1} , a_{2}+b_{2})・(c_{1} , c_{2})\\\\&=&(a_{1}+b_{1})・c_{1}+(a_{2}+b_{2})・c_{2}\\\\&=&a_{1}c_{1}+b_{1}c_{1}+a_{2}c_{2}+b_{2}c_{2}\\\\&=&(a_{1}c_{1}+a_{2}c_{2})+(b_{1}c_{1}+b_{2}c_{2})\\\\&=&\vec{a}・\vec{c}+\vec{b}・\vec{c}\end{eqnarray}$

となります。

$\underline{\bf{④について}}$

$③$と同様にして成分で考えて計算していくと、示すことができます。

$\underline{\bf{⑤について}}$

これも成分で考えて

$\begin{eqnarray}(k\vec{a})・\vec{b}&=&(ka_{1} , ka_{2})・(b_{1} , b_{2})\\&=&ka_{1}b_{1}+ka_{2}b_{2}\\\\&=&k(a_{1}b_{1}+a_{2}b_{2})\\\\&=&k(\vec{a}・\vec{b})\end{eqnarray}$

となります。
$\vec{a}・(k\vec{b})$についても、上記と同様に成分で考えて計算していくと示すことができます。

→目次へ戻る

2.外積

外積は高校数学では扱わないと思いますが、少しだけ触れることにします。
冒頭で述べたように高校物理では、ローレンツ力の計算に外積を用います。

ここで、ベクトルの内積と外積の違いについて触れておきます。

ベクトルの内積→ベクトルではなく実数

ベクトルの外積→ベクトル

先ほど述べたように、内積はベクトルの大きさと$\cos\theta$を用いて定義されており、計算結果はベクトルではなくスカラー(実数)となります。
これに対して、外積は計算結果が新たなベクトルとなります。
外積の内容は、2つのベクトルから新しいひとつのベクトルを生み出す操作となり、大きさだけではなく向きをもつことになります。
また、内積の表記は$\vec{a}・\vec{b}$だったのに対し、外積の表記は$\textcolor{red}{\vec{a}×\vec{b}}$となります。
次に、外積の定義について話していきます。

$\underline{\bf{図形的な定義}}$

今までは2次元(平面)で考えてきましたが、外積は3次元で考えます。
これは、後でも説明しますが外積は2つのベクトルのなす平面に垂直なベクトルとなるためです。

下図のように、$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$で考えます。
$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$のなす角を$\theta$とし、$\textcolor{red}{\vec{a}}\neq\vec{0}$　,　$\textcolor{blue}{\vec{b}}\neq\vec{0}$　,　$0^{\circ}\lt\theta\lt180^{\circ}$とします。

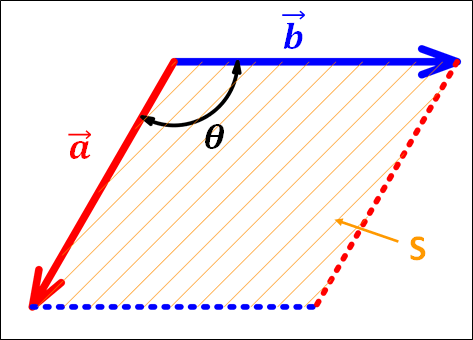
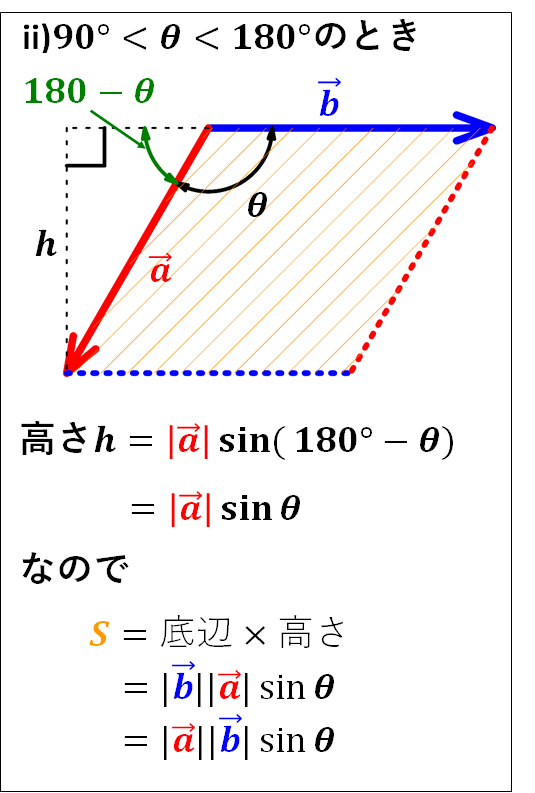
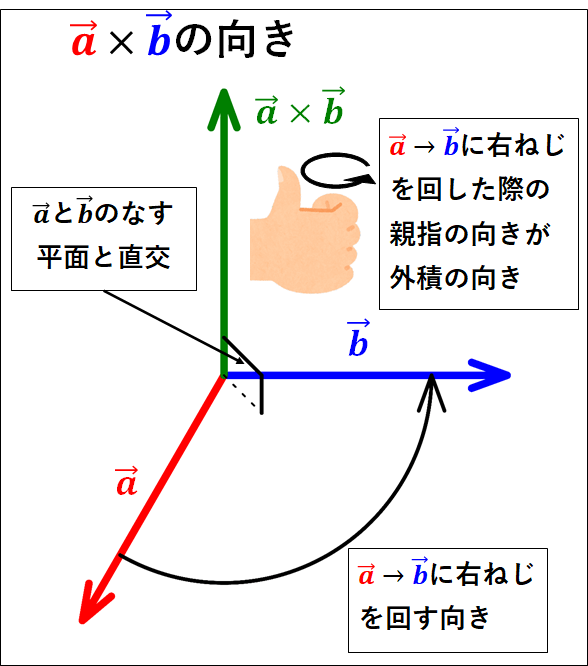
上図状態の時、外積$\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}$について、このベクトルの大きさは$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$によってできる平行四辺形の面積$\textcolor{#ffd700}{S}$と等しく、向きは$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$のなす平面に直行し、$\textcolor{red}{\vec{a}}$→$\textcolor{blue}{\vec{b}}$に右ねじを回すと進む向きとなります。

以下で、大きさと向きについて詳しく説明していきます。

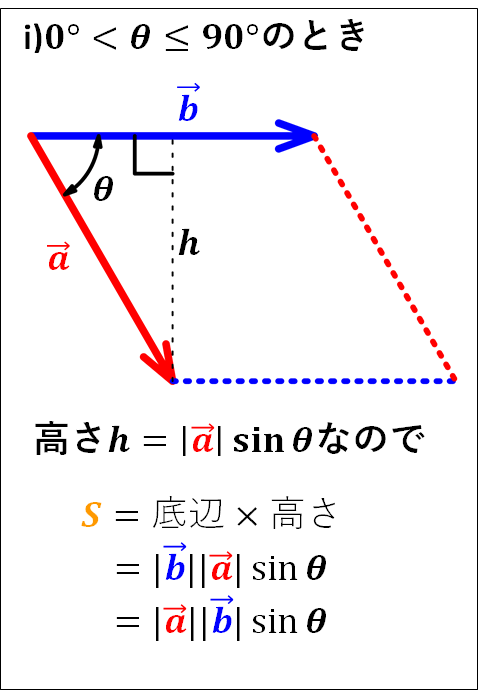
外積の大きさは2つのベクトルによってできる平行四辺形の面積であり、

$\bf{(平行四辺形の面積)=(底辺)×(高さ)}$

なので、以下のようになります。

三角関数についてはこちらも参考にしてください
→三角関数の定義と関係式
→三角関数の公式


図中の$\sin(180^{\circ}-\theta)$については、単位円で考えてもよいですが、三角関数の加法定理からみてみます。
加法定理から、

$\begin{eqnarray}\sin{(180^{\circ}-\theta)}&=&\sin{180^{\circ}}\cos\theta-\cos{180^{\circ}}\sin\theta\\&=&0×\cos\theta-(-1)×\sin\theta\\&=&\sin\theta\end{eqnarray}$

となります。


以上のことから、外積$\vec{a}×\vec{b}$の大きさは

$\textcolor{red}{|\vec{a}||\vec{b}|\sin\theta}$

となります。

次に外積の向きについてです。

外積$\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}$の向きは先ほど説明したように$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$のなす平面に直行し、$\textcolor{red}{\vec{a}}$→$\textcolor{blue}{\vec{b}}$に右ねじを回すと進む向きとなります。
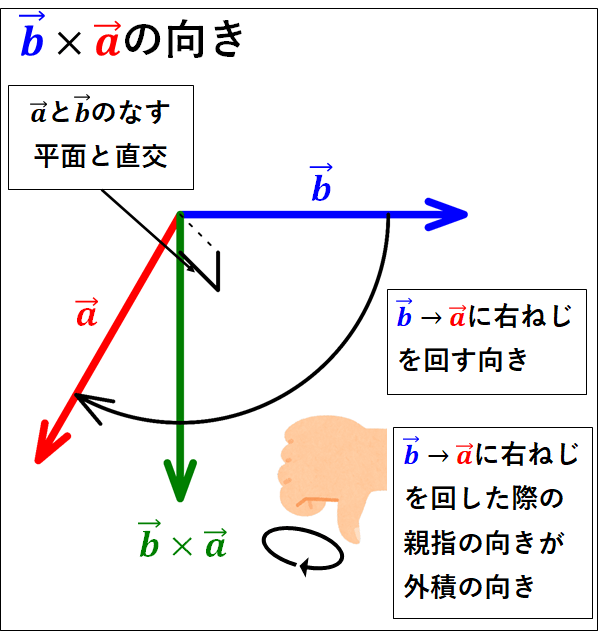
また、外積$\textcolor{blue}{\vec{b}}×\textcolor{red}{\vec{a}}$の向きは、$\textcolor{red}{\vec{a}}$と$\textcolor{blue}{\vec{b}}$のなす平面に直行し、$\textcolor{blue}{\vec{b}}$→$\textcolor{red}{\vec{a}}$に右ねじを回すと進む向きとなります。
このことから、外積$\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}$と外積$\textcolor{blue}{\vec{b}}×\textcolor{red}{\vec{a}}$は向きが逆となるので

$\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}\neq\textcolor{blue}{\vec{b}}×\textcolor{red}{\vec{a}}$

であり、

$\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}=-\textcolor{blue}{\vec{b}}×\textcolor{red}{\vec{a}}$

となります。
外積の向きのイメージ図を載せておきます。

※成分による外積の定義


成分による外積の定義は、

$\vec{a}=(a_{x} , a_{y} , a_{z})$、$\vec{b}=(b_{x} , b_{y} , b_{z})$とすると、

$\vec{a}×\vec{b}=(a_{y}b_{z}-a_{z}b_{y} , a_{z}b_{x}-a_{x}b_{z} , a_{x}b_{y}-a_{y}b_{x})$

となります。

今回は以上となります。
次回はベクトル関係の練習問題についての記事になります。

よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

→目次へ戻る


→高校物理へ戻る


→ホームへ戻る

関連記事
→ベクトルの演算と成分表示

→練習問題(内積/外積など)