投稿日:
【高校物理】ベクトル練習問題【高校数学】【ベクトル】【練習問題】
\(\require{color}\)
\(\require{cancel}\)
こちらは、ベクトルに関する練習問題となります。
ベクトルに関する記事は、こちらも参考にしてください。
→ベクトルの演算と成分表示
→ベクトルの内積と外積
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1-1.ベクトルの成分表示/問題
\(\mathbf{[問題1-1]}\)
次のベクトル\(\vec{r}\)を\(|\vec{r}|\)と\(\theta\)を用いて成分表示せよ。(\(\vec{r}=(x成分 , y成分)\)の形で)
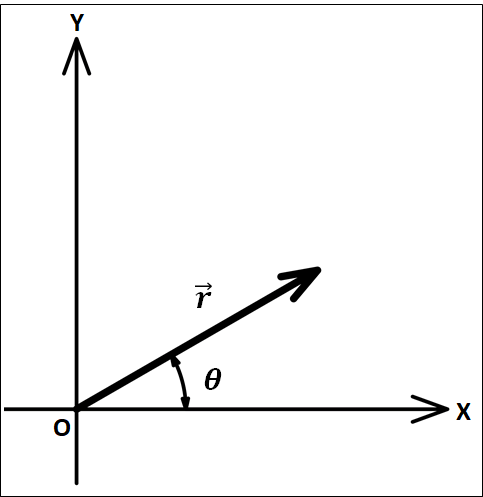
1-2.ベクトルの成分表示/解答
\(\mathbf{[問題1-1]の解答}\)
\(\vec{r}\)の終点から\(x\)軸に垂線を下してできる直角三角形に注目して考えます。
この直角三角形を下図のように、直角三角形\(OAB\)とします。
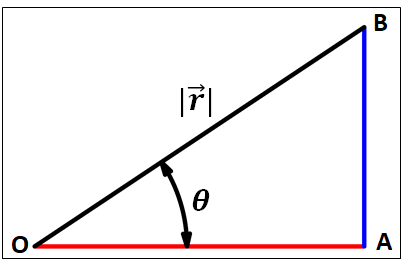
この直角三角形\(OAB\)において、\(\textcolor{red}{\overrightarrow{OA}}\)と\(\textcolor{blue}{\overrightarrow{AB}}\)を考えると、
\(\vec{r}=\textcolor{red}{\overrightarrow{OA}}+\textcolor{blue}{\overrightarrow{AB}}\)
となります。
また、\(\textcolor{red}{\overrightarrow{OA}}\)は\(x\)軸に沿っており、\(\textcolor{blue}{\overrightarrow{AB}}\)は\(y\)軸に沿っているので、\(\textcolor{red}{\overrightarrow{OA}}\)と\(\textcolor{blue}{\overrightarrow{AB}}\)はそれぞれ、\(\vec{r}\)の\(x\)成分と\(y\)成分となります。
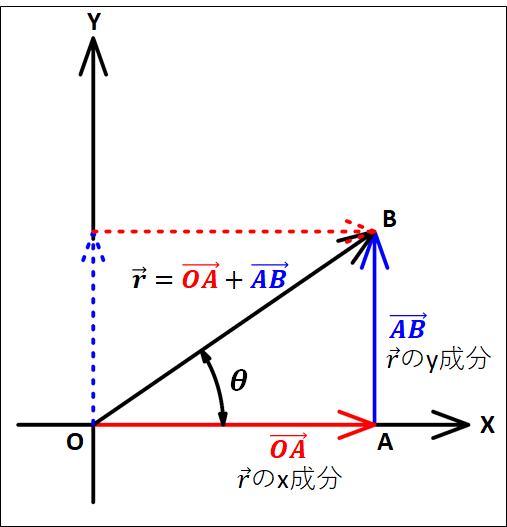
この\(\textcolor{red}{\overrightarrow{OA}}\)と\(\textcolor{blue}{\overrightarrow{AB}}\)を\(|\vec{r}|\)と\(\theta\)を用いて表します。
直角三角形\(OAB\)において三角関数を用いると、
\(\textcolor{red}{\overrightarrow{OA}}=|\vec{r}|\cos\theta\)
\(\textcolor{blue}{\overrightarrow{AB}}=|\vec{r}|\sin\theta\)
となります。
(三角関数についてはこちらも参考にしてください→三角関数の定義と関係式)
上式において、\(\textcolor{red}{\overrightarrow{OA}}\)と\(\textcolor{blue}{\overrightarrow{AB}}\)の大きさの情報は\(|\vec{r}|\)に、向きの情報はそれぞれ\(\cos\theta\)と\(\sin\theta\)に含まれます。
以上から、\(\vec{r}\)を成分表示すると、
\(\underline{\vec{r}=(|\vec{r}|\cos\theta , |\vec{r}|\sin\theta)}\)
となります。
2-1.内積/問題
\(\mathbf{[問題2-1]}\)
\(|\vec{a}|=2\)、\(|\vec{b}|=5\)、\(\vec{a}\)と\(\vec{b}\)のなす角\(\theta\)が\(60^{\circ}\)のとき、内積\(\vec{a}・\vec{b}\)を求めよ。
2-2.内積/解答
\(\mathbf{[問題2-1]の解答}\)
一応、状況を図示しておきます。
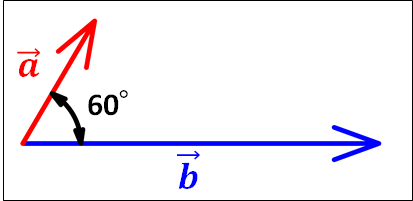
内積の定義は、
\(\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=|\textcolor{red}{\vec{a}}||\textcolor{blue}{\vec{b}}|\cos\theta\)
なので、求める内積は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}&=&2×5×\cos60^{\circ}\\&=&2×5×\frac{1}{2}\\&=&\underline{5}\end{eqnarray}}\)
となります。
解答は上記のように\(\underline{5}\)となりますが、ここで成分表示でも考えてみます。
問題文の状況を座標平面上で考えると、下図のようになります
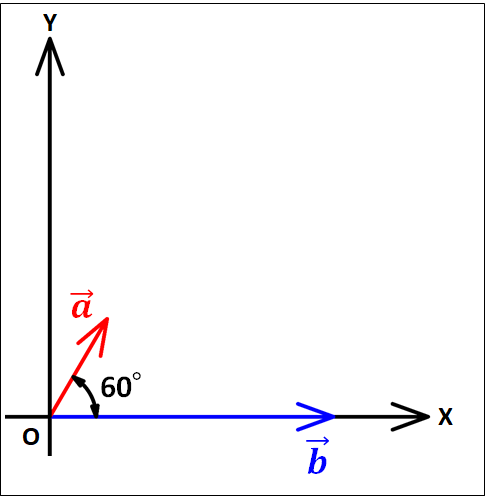
今回は、\(\textcolor{blue}{\vec{b}}\)を\(x\)軸に沿うように設定しましたが、始点が一致しており\(\textcolor{red}{\vec{a}}\)と\(\textcolor{blue}{\vec{b}}\)のなす角度が\(60^{\circ}\)であればどのように設定してもかまいません。
例えば、下図のように設定してもかまいません。
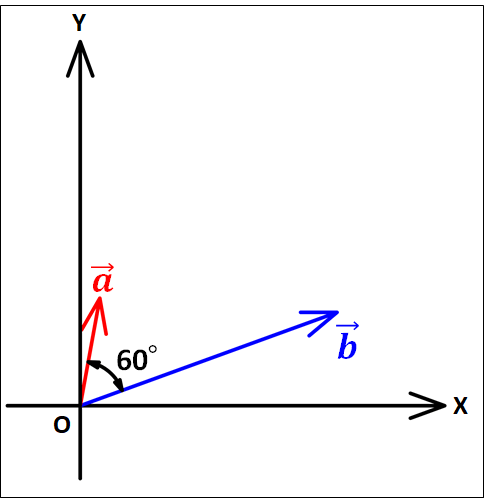
どのように設定してもかまいませんが、分かりやすく、計算しやすいように設定する方がよいでしょう。
本題に戻ります。
\(\textcolor{blue}{\vec{b}}\)を\(x\)軸に沿うような形で設定した座標平面において、\(\textcolor{red}{\vec{a}}\)と\(\textcolor{blue}{\vec{b}}\)を成分表示します。
\(\textcolor{red}{\vec{a}}\)は問題1-1と同様にして
\(\textcolor{red}{\vec{a}}\)の\(x\)成分:
\(\displaystyle{\begin{eqnarray}|\textcolor{red}{\vec{a}}|\cos60^{\circ}&=&2×\frac{1}{2}\\\\&=&1\end{eqnarray}}\)
\(\textcolor{red}{\vec{a}}\)の\(y\)成分:
\(\displaystyle{\begin{eqnarray}|\textcolor{red}{\vec{a}}|\sin60^{\circ}&=&2×\frac{\sqrt{3}}{2}\\\\&=&\sqrt{3}\end{eqnarray}}\)
\(\textcolor{blue}{\vec{b}}\)については
\(\textcolor{blue}{\vec{b}}\)の\(x\)成分:
図から\(\textcolor{blue}{\vec{b}}=5\)
\(\textcolor{blue}{\vec{b}}\)の\(y\)成分:
図から\(0\)
よって、それぞれのベクトルを成分表示すると、
\(\textcolor{red}{\vec{a}}=(\textcolor{red}{1} , \textcolor{red}{\sqrt{3}})\)
\(\textcolor{blue}{\vec{b}}=(\textcolor{blue}{5} , \textcolor{blue}{0})\)
となります。
成分表示による内積の定義は、
\(\textcolor{red}{\vec{a}}=(\textcolor{red}{a_{1}} , \textcolor{red}{a_{2}})\)
\(\textcolor{blue}{\vec{b}}=(\textcolor{blue}{b_{1}} , \textcolor{blue}{b_{2}})\)
とすると、
\(\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}=\textcolor{red}{a_{1}}\textcolor{blue}{b_{1}}+\textcolor{red}{a_{2}}\textcolor{blue}{b_{2}}\)
なので、内積は
\(\begin{eqnarray}\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}&=&\textcolor{red}{1}\textcolor{blue}{5}+\textcolor{red}{\sqrt{3}}\textcolor{blue}{0}\\\\&=&5\end{eqnarray}\)
となります。
また、成分表示で考えることと同じですが、基本ベクトルを用いた形で考えることもできます。
それぞれのベクトルを基本成分を用いて表すと、
\(\begin{eqnarray}\textcolor{red}{\vec{a}}&=&\textcolor{red}{1}×\vec{e_{1}}+\textcolor{red}{\sqrt{3}}×\vec{e_{2}}\\\\&=&\vec{e_{1}}+\textcolor{red}{\sqrt{3}}\vec{e_{2}}\end{eqnarray}\)
\(\begin{eqnarray}\textcolor{blue}{\vec{b}}&=&\textcolor{blue}{5}×\vec{e_{1}}+\textcolor{blue}{0}×\vec{e_{2}}\\\\&=&\textcolor{blue}{5}\vec{e_{1}}\end{eqnarray}\)
基本ベクトルについては、
\(\vec{e_{1}}\)←\(x\)軸の正方向の向きで大きさ\(1\)のベクトル
\(\vec{e_{2}}\)←\(y\)軸の正方向の向きで大きさ\(1\)のベクトル
よって、\(\vec{e_{1}}\)と\(\vec{e_{2}}\)のなす角は\(90^{\circ}\)であり、
\(\begin{eqnarray}\vec{e_{1}}・\vec{e_{2}}&=&|\vec{e_{1}}||\vec{e_{2}}|\cos90^{\circ}\\\\&=&1×1×0\\\\&=&0\end{eqnarray}\)
となります。
以上のことをふまえて、基本ベクトルを用いた形で外積を計算すると、
\(\begin{eqnarray}\textcolor{red}{\vec{a}}・\textcolor{blue}{\vec{b}}&=&(\vec{e_{1}}+\textcolor{red}{\sqrt{3}}\vec{e_{2}})・(\textcolor{blue}{5}\vec{e_{1}})\\\\&=&\textcolor{blue}{5}{|\vec{e_{1}}|}^2+\textcolor{blue}{5}\textcolor{red}{\sqrt{3}}\vec{e_{1}}・\vec{e_{2}}\\\\&=&\textcolor{blue}{5}×1^2+\textcolor{blue}{5}\textcolor{red}{\sqrt{3}}×0\\\\&=&5\end{eqnarray}\)
となります。
3-1.外積/問題
\(\mathbf{[問題3-1]}\)
下図において\(\textcolor{red}{|\vec{a}|=3}\)、\(\textcolor{blue}{|\vec{b}|=2}\)、\(\theta=30^{\circ}\)とする。
このとき、外積\(\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}\)の大きさ\(|\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}|\)を求め、その向きを図示せよ。
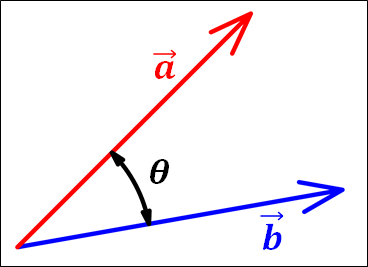
3-2.外積/解答
\(\mathbf{[問題3-1]の解答}\)
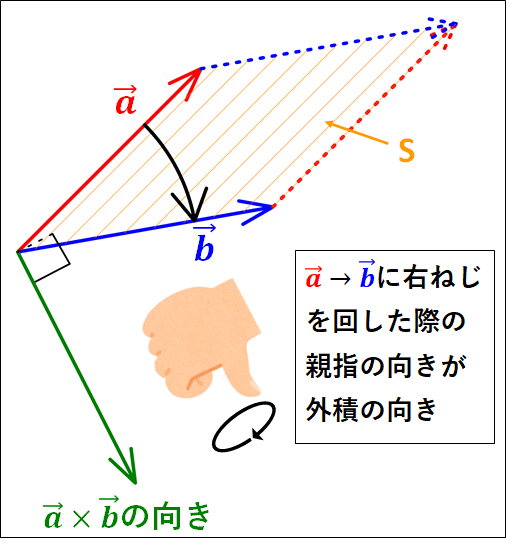
外積について、大きさは2つのベクトルのなす平行四辺形の面積であり、向きは\(\textcolor{red}{\vec{a}}\)と\(\textcolor{blue}{\vec{b}}\)のなす平面に直行し、\(\textcolor{red}{\vec{a}}\)→\(\textcolor{blue}{\vec{b}}\)に右ねじを回すと進む向きとなります。
上記の事柄から、大きさは下図の平行四辺形の面積\(\textcolor{#ffd700}{S}\)になります。
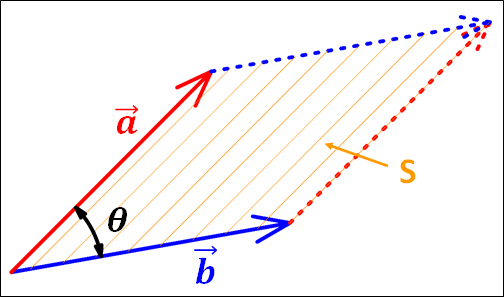
この面積\(\textcolor{#ffd700}{S}\)は、
\(\displaystyle{\begin{eqnarray}\textcolor{#ffd700}{S}&=&|\textcolor{red}{\vec{a}}||\textcolor{blue}{\vec{b}}|\sin\theta\\&=&\textcolor{red}{3}×\textcolor{blue}{2}×\sin30^{\circ}\\&=&\textcolor{red}{3}×\textcolor{blue}{2}×\frac{1}{2}\\&=&3\end{eqnarray}}\)
よって、\(\underline{外積の大きさ|\textcolor{red}{\vec{a}}×\textcolor{blue}{\vec{b}}|は3}\)
次に外積の向きですが、\(\textcolor{red}{\vec{a}}\)→\(\textcolor{blue}{\vec{b}}\)に右ねじを回したときに進む方向なので、図示すると以下のようになります。
ベクトルの練習問題は以上となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

関連記事
→ベクトルの演算と成分表示
→ベクトルの内積と外積

