投稿日:
【高校物理】万有引力【万有引力】【ケプラーの法則】【宇宙速度】
\(\require{color}\)
\(\require{cancel}\)
この記事では、ケプラーの法則や万有引力がどのように表されるか、また万有引力による位置エネルギーについて解説しています。
第1宇宙速度や第2宇宙速度についても触れていますが、詳しくは練習問題で扱っています。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.ケプラーの法則
\(\textcolor{red}{\bf{ケプラーの法則}}\)とは、ケプラーによって発見された惑星の運動に関する法則のこととなります。
第1法則から第3法則まであるので、これらについてみていきます。
\(\underline{\bf{○第1法則}}\)
惑星は、太陽を1つの焦点とする楕円軌道を描く。
これは、説明のとおり惑星は太陽を1つの焦点とする楕円軌道で太陽の周りを回りますよというものです。
\(\underline{\bf{○第2法則}}\)
惑星と太陽を結ぶ線分が、一定時間に描く面積は一定である。
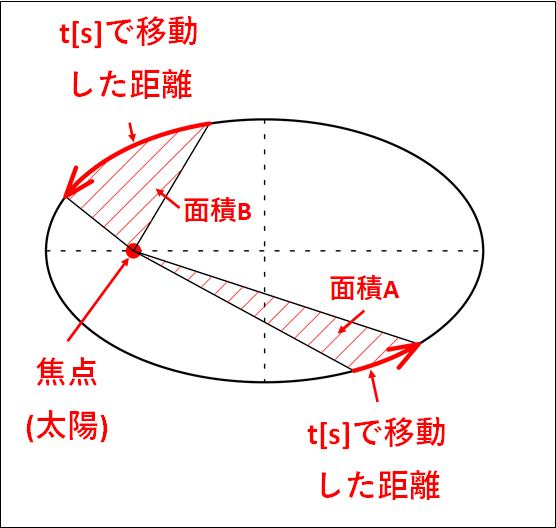
上図において、2つの赤い矢印は、\(t[s]\)の間に惑星が楕円軌道上を動いた距離となります。
このとき、惑星と焦点(太陽)を結ぶ線分が一定時間に描く面積は、それぞれ\(\textcolor{red}{A , B}\)となります。
第2法則は、この面積について
\(\textcolor{red}{\bf{面積A=面積B}}\)
になりますよ、というものです。
また、第2法則は
\(\textcolor{red}{\bf{面積速度一定の法則}}\)
ともいいます。
先ほど見た図では\(t[s]\)で描く面積が\(A\)や\(B\)でしたが、面積速度とは、\(t[s]\)ではなく単位時間(1秒)で描く面積のこととなります。
特に、下図のような状況を考えます。
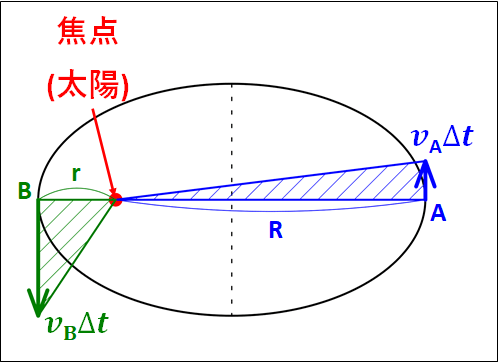
微小時間\(\Delta{t}\)の間に、点Aと点Bにおける速度がそれぞれ\(\textcolor{blue}{v_A}\)と\(\textcolor{green}{v_B}\)である物体が進む距離はそれぞれ\(\textcolor{blue}{v_A\Delta{t}}\)と\(\textcolor{green}{v_B\Delta{t}}\)となります。
微小時間なので、図のように点A、Bにおける楕円の接線の向きに進んだと近似してあります。
また、焦点(太陽)から点A、Bそれぞれまでの距離を\(\textcolor{blue}{R}\)、\(\textcolor{green}{r}\)としています。
このとき、青色の斜線部分面積を\(\textcolor{blue}{\Delta{S_A}}\)、緑色の斜線部分面積を\(\textcolor{green}{\Delta{S_B}}\)とすると、三角形の面積の式から
\(\displaystyle{\textcolor{blue}{\Delta{S_A}=\frac{1}{2}Rv_A\Delta{t}}}\)
\(\displaystyle{\textcolor{green}{\Delta{S_B}=\frac{1}{2}rv_B\Delta{t}}}\)
このとき、微小時間\(\Delta{t}\)の間に描いた面積は等しいので
\(\displaystyle{\begin{eqnarray}&&\textcolor{blue}{\Delta{S_A}}=\textcolor{green}{\Delta{S_B}}\\\\{\Leftrightarrow}&&\textcolor{blue}{\frac{1}{2}Rv_A\Delta{t}}=\textcolor{green}{\frac{1}{2}rv_B\Delta{t}}\end{eqnarray}}\)
この面積を微小時間で割ったものが面積速度なので、両辺微小時間\(\Delta{t}\)で割って
\(\displaystyle{\textcolor{blue}{\frac{1}{2}Rv_A}=\textcolor{green}{\frac{1}{2}rv_B}}\)
上式は面積速度(単位時間あたりに描く面積)が等しいことを表しています。
また、上図の点Aは太陽から最も遠ざかる点であり、この点を\(\textcolor{blue}{\bf{遠日点}}\)といいます。
点Bは太陽に最も近づく点であり、この点を\(\textcolor{red}{\bf{近日点}}\)といいます。
同じ時間に移動した点が描く面積が一定となることから、太陽の周りを楕円軌道で運動する惑星の速さは、\(\textcolor{blue}{\bf{遠日点}}\)で最小、\(\textcolor{red}{\bf{近日点}}\)で最大となります。
ちなみに、一般の位置における面積速度を考えてみます。
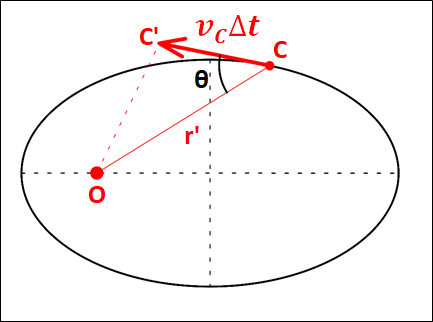
こちらも先ほどと同様にして、点Cにおける速度を\(v_C\)、微小時間\(\Delta{t}\)の間に進んだ距離は、点Cにおける楕円の接線方向に\(v_C\Delta{t}\)となります。
また、\(OC=r^{\prime}\)とし、速度の方向と\(OC\)のなす角を\(\theta\)とします。
このとき、三角形\(OCC^{\prime}\)に注目します。
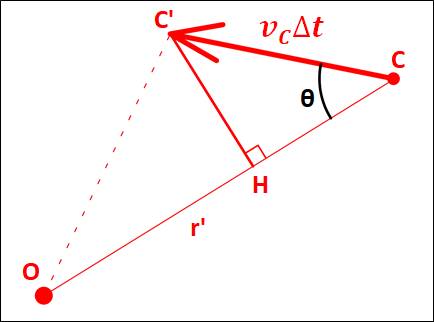
\(C^{\prime}\)から線分\(OC\)に垂直な線分\(C^{\prime}H\)を引きます。
そうすると、\(CC^{\prime}H\)は\(CC^{\prime}\)を斜辺とする直角三角形となるので、三角関数から
\(\displaystyle{\begin{eqnarray}C^{\prime}H&=&CC^{\prime}×\sin\theta\\\\&=&v_C\Delta{t}\sin\theta\end{eqnarray}}\)
※三角関数についてはこちら
→三角関数の定義と関係式
以上から、三角形\(OCC^{\prime}\)は、
底辺:
\(OC=r^{\prime}\)
高さ:
\(C^{\prime}H=v_C\Delta{t}\sin\theta\)
の三角形なので、この三角形の面積は、
\(\displaystyle{\frac{1}{2}r^{\prime}v_C\Delta{t}\sin\theta}\)
よって、面積速度は\(\Delta{t}\)で割って
\(\displaystyle{\frac{1}{2}r^{\prime}v_C\sin\theta}\)
となります。
\(\underline{\bf{○第3法則}}\)
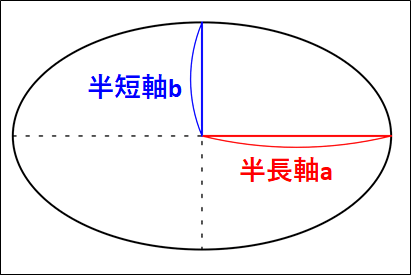
惑星の公転周期\(T\)の2乗は、楕円軌道の半長軸\(a\)の3乗に比例する。
半長軸とは、楕円における長い方の直径の半分の長さのことです。
ちなみに、短い方の直径を短軸といいます。
また、上記の事柄を式で表すと、比例定数を\(k\)として
\(\displaystyle{T^2=ka^3}\)
となります。
上式を変形すると
\(\displaystyle{\begin{eqnarray}&&T^2=ka^3\\\\{\Leftrightarrow}&&\frac{T^2}{a^3}=k (一定)\end{eqnarray}}\)
となります。
このことから、1つめの惑星の周期を\(T_1\)、楕円軌道の半長軸を\(a_1\)とし、同様にして2つめ、3つめ…の惑星についても\(T_2,T_3,\cdots\)、\(a_2,a_3,\cdots\)とします。
これらの惑星について、
\(\displaystyle{\frac{T^2}{a^3}}\)
は一定となるので
\(\displaystyle{\frac{T_1^2}{a_1^3}=\frac{T_2^2}{a_2^3}=\frac{T_3^2}{a_3^3}=\cdots}\)
が成り立ちます。
第3法則については、練習問題でも扱っています。
2.万有引力の法則
\(\textcolor{red}{\bf{万有引力}}\)は、質量をもつ物体間にはたらく力で、お互いに引きつける向きにはたらきます。
2物体間にはたらく万有引力の大きさ\(F[N]\)は、2物体の質量をそれぞれ\(m_1,m_2\)とすると、この質量の積に比例し物体間の距離\(r[m]\)の2乗に反比例します。
物体間の距離\(r[m]\)は中心間の距離を用います。
また。万有引力は\(\textcolor{red}{\bf{保存力}}\)となります。
※保存力と非保存力についてはこちら
→仕事とエネルギー
なので、仕事とエネルギーの等価性原理から、万有引力がした仕事を左辺のエネルギー項に移項すると、万有引力による位置エネルギーの変化量になります。
万有引力の大きさ\(F\)を式で表すと、比例定数\(G\)を用いて、
\(\displaystyle{F=G\frac{m_1m_2}{r^2}}\)
となります。
この比例定数\(G\)を\(\textcolor{green}{\bf{万有引力定数}}\)といいます。
単位は、
\(\displaystyle{F[N]=G\frac{m_1[kg]m_2[kg]}{r^2[m^2]}}\)
から
\(\displaystyle{G=F[N]×\frac{r^2[m^2]}{m_1m_2[kg^2]}}\)
となるので、\([N・m^2/kg^2]\)となります。
※未知の単位を求める次元解析についてはこちら
→単位の計算・換算練習問題2(次元解析と解答確認)
練習問題では、万有引力の法則を用いてケプラーの第3法則を求めています。
3.万有引力と重力
地球上の物体にはたらく重力は、物体と地球との間にはたらく万有引力と、地球の自転による遠心力との合力となります。
ですが、地球の自転による遠心力は、万有引力に比べてとても小さいので無視できます。
よって、”地球上の物体にはたらく重力は、地球と物体の間の万有引力であると考えてよい”です。
地球と物体の質量をそれぞれ\(M,m\)とし、地球の半径を\(R\)地上での重力加速度を\(g\)とすると、\(\textcolor{red}{\bf{地表において}}\)
\(\displaystyle{\begin{eqnarray}&&mg=G\frac{Mm}{R^2}\\\\{\Leftrightarrow}&&g=G\frac{M}{R^2}\end{eqnarray}}\)
となります。
4.第1宇宙速度
\(\textcolor{red}{\bf{第1宇宙速度}}\)とは、人工衛星が地表近くを円運動する速さのことです。
詳しくは練習問題で扱いますが、人工衛星が地表近くを等速円運動するとして求めます。
5.万有引力による位置エネルギー
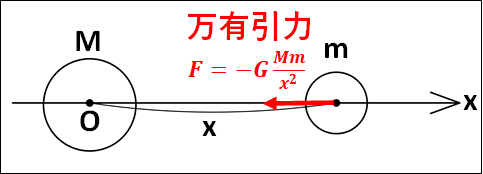
上図は、距離が\(x\)だけはなれた質量\(M\)と\(m\)の物体について考えたものです。
質量\(m\)の物体には万有引力が、質量\(M\)の物体に引き付けられる向きにはたらいています。
万有引力の大きさは、
\(\displaystyle{F=G\frac{Mm}{x^2}}\)
から、\(x\)が大きくなるほど、つまり物体同士が離れるほど小さくなり、十分に遠方だとほとんど\(0\)となります。
万有引力による位置エネルギーの基準は、万有引力が\(0\)となるような十分に遠方の点である無限遠点とすることが多いです。
図の状態において、質量\(m\)の物体の運動方程式は
\(\displaystyle{ma=-G\frac{Mm}{x^2}}\)
これを\(\textcolor{green}{\bf{エネルギー積分}}\)していきます。
※エネルギー積分についてはこちらの記事の、「4.運動エネルギーと仕事の関係」も参考にしてください。
→仕事とエネルギー
先ほどの運動方程式の両辺に\(v\)を掛けて
\(\displaystyle{m\textcolor{red}{v}a=-G\frac{Mm}{x^2}\textcolor{red}{v}}\)
速度と加速度の定義式
\(\displaystyle{v=\frac{dx}{dt} , a=\frac{dv}{dt}}\)
から、運動方程式は
\(\displaystyle{\begin{eqnarray}&&m\textcolor{red}{v}a=-G\frac{Mm}{x^2}\textcolor{red}{v}\\\\{\Leftrightarrow}&&mv\frac{dv}{dt}=-G\frac{Mm}{x^2}\frac{dx}{dt}\end{eqnarray}}\)
※変位・速度・加速度についてはこちら
→変位・速度・加速度
ここで、
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\left\{\frac{1}{2}mv^2\right\}&=&\frac{dv}{dt}\frac{d}{dv}\left\{\frac{1}{2}mv^2\right\}\\\\&=&mv\frac{dv}{dt}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\frac{d}{dt}\left\{G\frac{Mm}{x}\right\}&=&\frac{dx}{dt}\frac{d}{dx}\left\{G\frac{Mm}{x}\right\}\\\\&=&-G\frac{Mm}{x^2}\frac{dx}{dt}\end{eqnarray}}\)
となるので、
\(\displaystyle{\begin{eqnarray}&&mv\frac{dv}{dt}=-G\frac{Mm}{x^2}\frac{dx}{dt}\\\\{\Leftrightarrow}&&\frac{d}{dt}\left\{\frac{1}{2}mv^2\right\}=\frac{d}{dt}\left\{G\frac{Mm}{x}\right\}\\\\{\Leftrightarrow}&&\frac{d}{dt}\left\{\frac{1}{2}mv^2+\left(-G\frac{Mm}{x}\right)\right\}=0\end{eqnarray}}\)
※\(x^{-2}\)の微積についてはこちら
→微分法とその応用
→積分法の応用
上記から、万有引力による位置エネルギー\(U\)は
\(\displaystyle{\textcolor{green}{U=-G\frac{Mm}{x}}}\)
で表され、さらに力学的エネルギーは保存することが分かります。

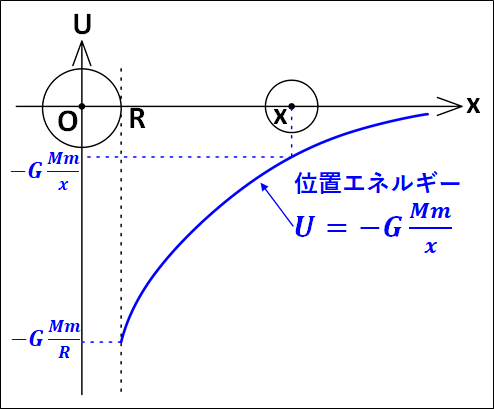
また、中心間距離\(x\)と万有引力による位置エネルギー\(U\)の関係を表したグラフは下図のようになります。
6.第2宇宙速度
\(\textcolor{red}{\bf{第2宇宙速度}}\)とは、物体が地球の重力(万有引力)を振り切って、どこまでも遠くに飛んでいくように投げる際に必要な最低限の速度のことです。
こちらも詳しくは、練習問題で扱っています。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


