投稿日:
【高校物理】剛体【剛体】
\(\require{color}\)
\(\require{cancel}\)
この記事では剛体全般について解説しています。
内容としては、剛体と質点の違いや、力のモーメントの計算方法、物体の重心の求め方などになります。
物体の重心も、力のモーメントとつりあいから求める方法と、座標から求める方法を解説しています。
また、数学的にはどのように重心を求めるかについても紹介しています。
練習問題の方で解説しているものもありますので、そちらもご覧ください。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.剛体と質点
力についての解説記事で扱ってきた物体は、全て\(\textcolor{red}{\bf{質点}}\)となります。
しかし、今回は\(\textcolor{red}{\bf{剛体}}\)というものを扱っていきます。
“質点”と”剛体”の違いは、以下のようになります。
質点:
形や大きさを無視し、質量が1点に集中したもの
剛体:
形や大きさを持ち、力を加えても変形しない物体(回転についても考える必要がある)
2.力のモーメント(トルク)
物体にはたらく力の大きさ\(F\)と、回転軸から力の作用線におろした垂線の長さ\(l\)(うでの長さ)との積は、剛体を回転軸まわりに回転させようとする能力の大きさを表しています。
これを\(\textcolor{red}{\bf{力のモーメント}}\)といいます。
力については、大きいほど回転しやすいということが分かると思います。
うでの長さについては、例えばスパナなど(扱ったことがないかもしれませんが)何かを回したいときに、なるべく遠くをもって回転させようと力を加えると、楽に回せるという経験があるかもしれません。
力のモーメントの正負は、”反時計回りを正、時計回りを負”とします。
これは、三角関数において単位円上の角度\(\theta\)の正負とおなじ考えとなります。
以上のことから、力のモーメント\(M\)は
\(M={\bf{(符合)×力×うでの長さ}}\)
で表されます。
単位は、力の単位である\(N\)と長さの単位である\(m\)を掛けて、
\(\displaystyle{\bf{\begin{eqnarray}{\bf{力×長さ}}&=&N×m\\\\&=&N・m\end{eqnarray}}}\)
から、\(N・m\)(ニュートンドットメートル)となります。
下記に、力のモーメントの例を載せておきます。
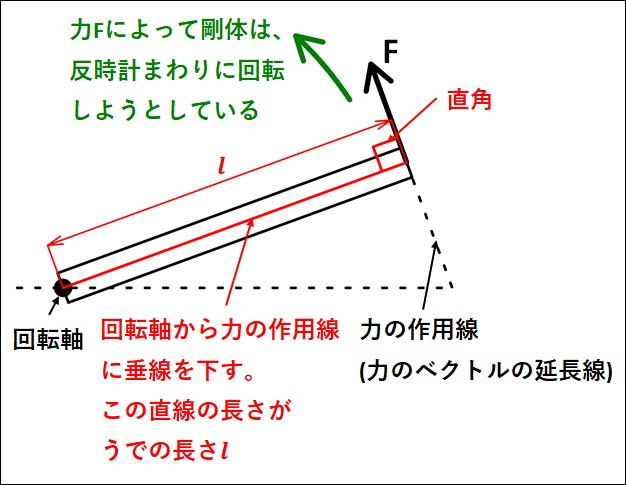
上図の場合、力\(F\)による力のモーメント\(M\)は
\(\displaystyle{M=-Fl}\)
となります。
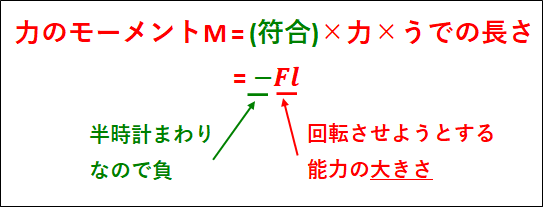
回転の方向は、回転軸をピンで止め、かかっている力の方向に物体をはじいたときに回る方向となります。
3.剛体のつりあい
剛体は質点と異なり形と大きさをもつので、回転についてのつりあい(モーメントのつりあい)も考える必要があります。
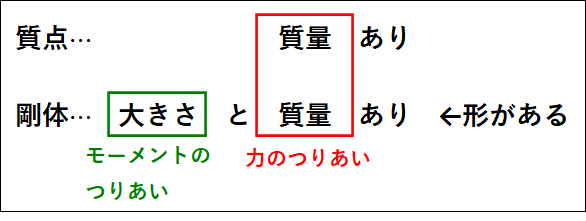
モーメントがつりあう(回転しない)条件は、剛体にかかっている力のモーメントの和が\(0\)というものになります。
物体に複数の力がかかっており、この力によるモーメントをそれぞれ
\(M_1,M_2,M_3,\cdots\)
とすると、モーメントのつりあいの式は
\(M_1+M_2+M_3+\cdots=0\)
となります。
モーメントのつりあいを考える際には、回転軸を設定する必要がありますが、問題文で特に指定されていなければ、どこに設定してもよいです。
4.剛体にはたらく力の合成
定規やコンパスを使わずに、剛体にかかっている合力とその作用点を求めるには、
①力の大きさだけの和を考える
②力のはたらく位置を求める
\(\textcolor{green}{\bf{(モーメントが等しい)}}\)
という操作を行います。
具体的にどのように求めるかについては、練習問題の方で解説します。
5.偶力
\(\textcolor{red}{\bf{同じ大きさ}}\)で\(\textcolor{red}{\bf{反対向き}}\)の\(\textcolor{red}{\bf{平行}}\)な2力は、物体を移動させるはたらきはありませんが、物体を回転させるはたらきはもちます。
このような1組の力を”\(\textcolor{red}{\bf{偶力}}\)”といいます。
また、この2力の任意の点まわりの力のモーメントの和\(M^{\prime}\)を\(\textcolor{red}{\bf{偶力モーメント}}\)といいます。
例として、下図のような状況を考えます。
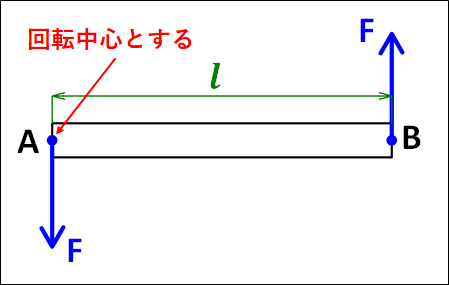
上図は力\(F\)が”同じ大きさ”、”反対向き”、”平行”に働いているので”偶力”となります。
力の和と、モーメントの和を実際に計算してみます。
\(\bf{\underline{○力の和}}\)
力は上下方向にかかっているので、どちらを正にとっても良いですが上向きを正としておきます。
そうすると、\(A\)点にかかっている力は\(-F\)、\(B\)点にかかっている力は\(+F\)となります。
なので、これらの力の和は
\((-F)+(+F)=0\)
となります。
上式の結果から、上下方向の力の和(合力)は\(0\)なので、つりあっていることがわかります。
このことから、物体を移動させるはたらきがないことが分かります。
\(\bf{\underline{○モーメントの和}}\)
次に、モーメントの和を考えていきます。
回転中心は、どこにとっても良いですが点\(A\)としておきます。
そうすると、点\(A\)を回転中心としたときの点\(A\)部分にかかっている力のモーメントは、うでの長さが\(0\)となるので
\(F×0\)
点\(A\)を回転中心としたときの点\(B\)部分にかかっている力のモーメントは、うでの長さが\(l\)、点\(A\)にピンをさして点\(B\)部分にかかっている力の方向に物体をはじくと反時計まわりに回転するので、符合は正となります。
よって、
\((+)F×l\)
となります。
これらモーメントの和を計算すると
\((F×0)+(+Fl)=+Fl\)
この\(+Fl\)が\(\textcolor{red}{\bf{偶力モーメント}}\)となります。
この場合、上記の偶力モーメントは剛体を反時計まわりに回転させようとするはたらきをもっています。(符合がプラスなので)
6.重心
剛体を無数の小さな部分の集まりと考えると、この小さな各部分には重力がはたらいています。
この\(\textcolor{red}{\bf{各部分にはたらく重力の和}}\)を、その物体の”\(\textcolor{red}{\bf{重心}}\)”といいます。
※
質点では、大きさがないので重力は1点にしかはたらかない
また、物体を重心で支えれば、回転せずにつりあうので、”重心は物体全体の全質量が集まっている点とみなすこともできます”。
\(\bf{\underline{○重心の求め方}}\)
\(\bf{i)モーメントと力のつりあいで考える}\)
\(x\)軸上に質量がそれぞれ\(m_1,m_2,m_3\)の物体があるとします。
この物体の原点(回転中心)からの距離をそれぞれ\(x_1,x_2,x_3\)とします。
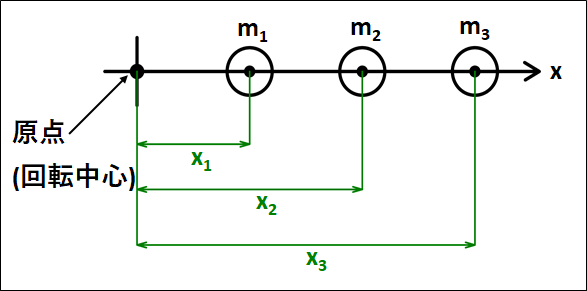
\(m_1,m_2,m_3\)にはそれぞれ重力がかかっており、重心では物体が回転せずにつりあうので、原点から重心までの距離を\(x_g\)、重心で支えている力を\(F\)とします。
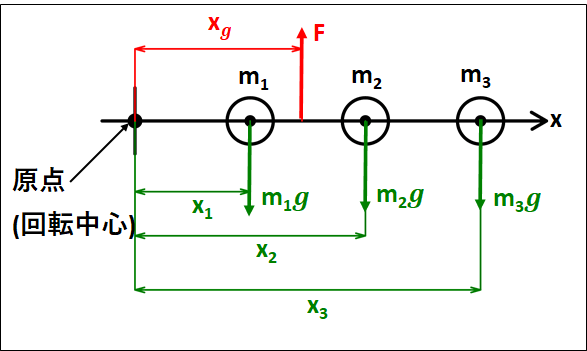
上図より、力のつりあいから
\(\displaystyle{\begin{eqnarray}F&=&m_1g+m_2g+m_3g\\\\&=&(m_1+m_2+m_3)g\cdots①\end{eqnarray}}\)
モーメントのつりあいから
\(\displaystyle{\small{\begin{eqnarray}&&(-m_1gx_1)+(-m_2gx_2)+(-m_3gx_3)+(+Fx_g)=0\\\\\Leftrightarrow&&Fx_g=(m_1x_1+m_2x_2+m_3x_3)g\cdots②\end{eqnarray}}}\)
\(①\)を\(②\)に代入して、
\(\displaystyle{\begin{eqnarray}&&(m_1+m_2+m_3)g・x_g=(m_1x_1+m_2x_2+m_3x_3)g\\\\\Leftrightarrow&&x_g=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}\end{eqnarray}}\)
上記が回転中心からの重心の距離の公式になります。(物体が3つの場合)
\(\textcolor{green}{\bf{重心の公式}}\)
\(\displaystyle{\textcolor{green}{x_g=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}}}\)
公式を、文字で表すと
\(\displaystyle{\bf{(重心の距離)=\frac{各物体の質量×各物体の距離 の和}{全質量}}}\)
となります。
上記は、物体が3つの場合ですが、4つや5つになった場合でも、分子に4つめや5つめの(質量×うでの長さ)を足していき、分母に4つや5つめの質量を足すと重心を求めることができます。
また、今回は\(x\)軸上(同一直線上)に並んだ物体に関して求めましたが、この場合(y)軸方向のうでの長さが\(0\)となるので、\(y\)軸に関して重心を求めると\(0\)となります。
よって、物体の重心は\(x\)軸からの距離が\(0\)の部分、すなわち\(x\)軸上にあるということになりますが、\(y\)軸方向にも物体がある場合、上記の公式を\(y\)軸方向の物体に関して立てることで、\(y\)軸方向の重心を求めることができます。
\(\bf{ii)座標で考える}\)
重心は、物体の全質量が集まっている点であるとみなせます。
また、重心ではモーメントがつりあうので、以下のことが成り立ちます。
\(\small{\bf{(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和}}\)
上式を念頭において、下図のような状況を考えます。
3つの物体は、質量がそれぞれ\(m_1,m_2,m_3\)とします。
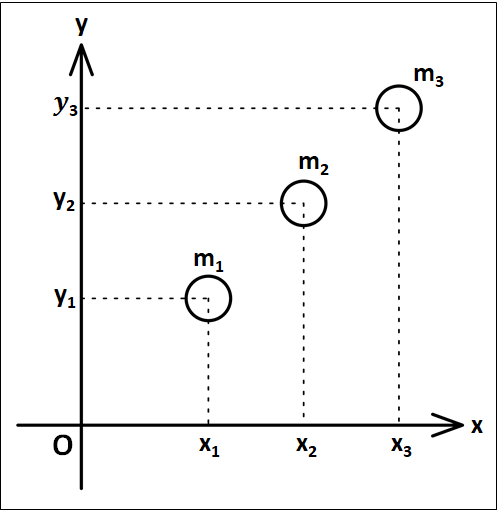
上図において、重心の\(x\)座標を\(x_g\)、\(y\)座標を\(y_g\)とします。
\(\small{\bf{(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和}}\) から、
\(x\)軸方向の重心座標\(x_g\)は
\(Mx_g=m_1x_1+m_2x_2+m_3x_3\)
ここで\(M\)は全質量で、\(M=m_1+m_2+m_3\)です。
これを先ほどの式に代入して、
\(\displaystyle{\begin{eqnarray}&&(m_1+m_2+m_3)x_g=m_1x_1+m_2x_2+m_3x_3\\\\\Leftrightarrow&&x_g=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}\end{eqnarray}}\)
となります。
同様にして、\(y\)軸方向の重心座標\(y_g\)は、
\(\displaystyle{\begin{eqnarray}&&My_g=m_1y_1+m_2y_2+m_3y_3\\\\\Leftrightarrow&&(m_1+m_2+m_3)y_g=m_1y_1+m_2y_2+m_3y_3\\\\\Leftrightarrow&&y_g=\frac{m_1y_1+m_2y_2+m_3y_3}{m_1+m_2+m_3}\end{eqnarray}}\)
となります。
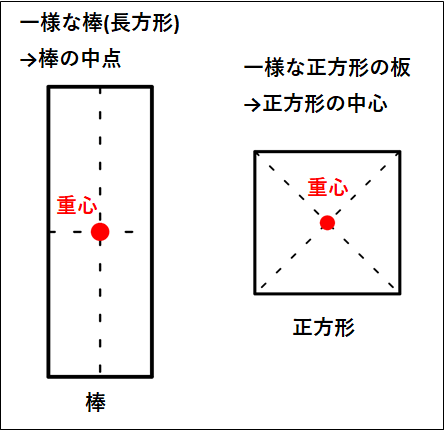
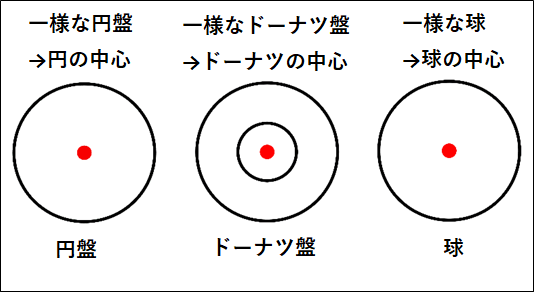
\(\bf{\underline{代表的な一様な物体の重心}}\)
代表的な一様な物体の重心位置を載せておきます。
だいたい物体の中心になるので覚えれないことはないと思います。
7.一様な棒と半球の重心(余談)
興味がない人は読み飛ばしていただいてかまいません。
積分を用いるので、積分に関してはこちらも参考にしてください
→積分法
→積分法の応用
※
大学的に…
一様な棒の重心はどう求めるのか?
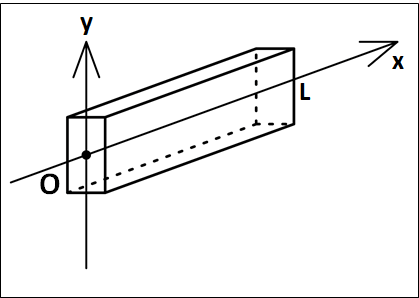
\(\bf{\underline{○一様な棒の重心}}\)
以下のように座標を設定します。
真横から見ると、次のようになります。
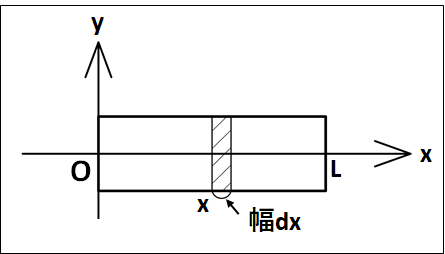
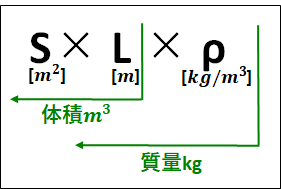
棒の断面積を\(S[m^2]\)、棒の長さを\(L[m]\)、棒の密度を\(ρ[kg/m^3]\)とします。
このとき、棒の全質量\(M\)は
\(M=S[m^2]×L[m]×ρ[kg/m^3]=SLρ[kg]\)
となります。
横から見た図のように、原点から\(x\)だけ離れた部分の微小幅\(dx\)部分の質量は、
\(S[m^2]×dx[m]×ρ[kg/m^3]=ρSdx[kg]\)
となります。
これより、微小部分の(質量×座標)は
\(ρSdx×x=ρSxdx\)
です。
これを\(x=0\)から\(x=L\)まで足すと、(各物体の質量×各物体の座標)の和、となり
\(\displaystyle{\int_0^L{ρSx}dx}\)
と表されます。
以上から、
(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和
を用いて、重心座標を\(x_g\)とすると、
\(\displaystyle{\begin{eqnarray}&&M×x_g=\int_0^L{ρSx}dx\\\\\Leftrightarrow&&SLρ×x_g=ρS\int_0^L{x}dx\\\\\Leftrightarrow&&L×x_g=\left[\frac{1}{2}x^2\right]_0^L\\\\\Leftrightarrow&&Lx_g=\frac{1}{2}L^2\\\\\Leftrightarrow&&x_g=\frac{1}{2}L\end{eqnarray}}\)
以上のことから、\(x\)軸方向の重心は、棒の中央が重心となることが分かります。
(全体の長さ\(L\)の半分の位置が重心)
\(\bf{\underline{○半球の重心}}\)
半径が\(r\)の半球の重心を求めてみます。
以下のように座標を設定し、\(y\)軸方向の重心である\(y_g\)について考えてみます。
半球は一様で、密度は\(ρ[kg/m^3]\)とします。
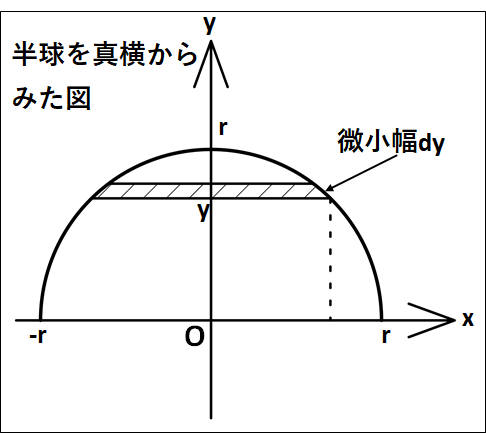
ここで、半径が\(r\)である円の方程式は
\(x^2+y^2=r^2\)
です。
図から、\(y\)座標の値が\(y\)である部分の\(x\)座標は、
\(\displaystyle{\begin{eqnarray}&&x^2+y^2=r^2\\\\\Leftrightarrow&&x^2=r^2-y^2\end{eqnarray}}\)
より、
\(x=±\sqrt{r^2-y^2}\)
これが、これから考える微小部円盤の、円の半径となります。
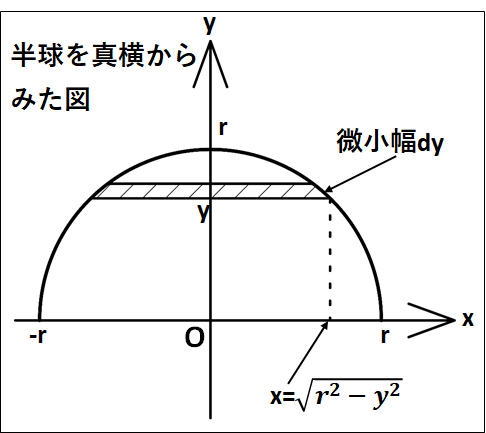
次に、微小幅\(dy\)部分の円盤の質量を考えていきます。
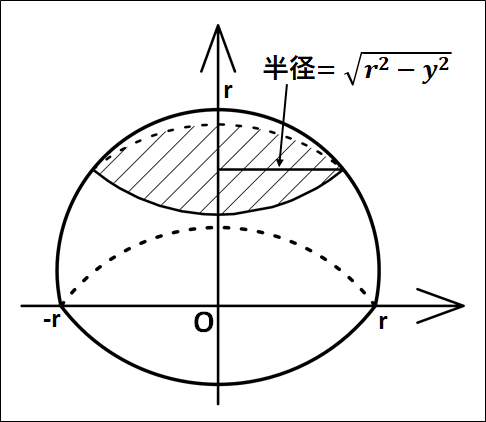
斜線部の円の半径は、先ほど求めた\(\displaystyle{\sqrt{r^2-y^2}}\)となります。
厚さ\(dy\)で半径が\(\displaystyle{\sqrt{r^2-y^2}}\)の微小円盤の質量は(円の面積×厚さ×密度)から、
\(\displaystyle{\begin{eqnarray}&&\pi{x^2}・dy・ρ\\\\=&&\pi{ρ}(r^2-y^2)dy\end{eqnarray}}\)
これより、(質量×\(y\)座標)は、
\(\displaystyle{\pi{ρ}(r^2-y^2)ydy}\)
となります。
全質量\(M\)は、球の質量の半分なので、(体積×密度÷2)から
\(\displaystyle{\begin{eqnarray}M&=&\frac{4\pi{r^3}}{3}・ρ×\frac{1}{2}\\\\&=&\frac{2}{3}\pi{ρ}r^3\end{eqnarray}}\)
以上から、一様な棒の重心を求めたときと同様にして、
(全質量)×(重心座標)=(各物体の質量×各物体の座標)の和
を用いて
\(\displaystyle{\begin{eqnarray}&&M・y_g=\int_0^r{\pi{ρ}(r^2-y^2)y}dy\\\\\Leftrightarrow&&\frac{2}{3}\pi{ρ}r^3y_g=\pi{ρ}\int_0^r{(r^2y-y^3)}dy\\\\\Leftrightarrow&&\frac{2}{3}r^3y_g=\left[\frac{1}{2}r^2y^2-\frac{1}{4}y^4\right]_0^r\\\\\Leftrightarrow&&\frac{2}{3}r^3y_g=\frac{1}{2}r^4-\frac{1}{4}r^4=\frac{1}{4}r^4\\\\\Leftrightarrow&&y_g=\frac{3}{8}r\end{eqnarray}}\)
となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


