投稿日:
【高校物理】運動量と力積【運動量】【力積】【運動量保存則】【反発係数】
\(\require{color}\)
\(\require{cancel}\)
運動量と力積の関係は、運動方程式を変形していくことで導くことができます。
この記事では、上記の運動量と力積の関係や、二物体以上の運動方程式に関して内力化できる際に成り立つ運動量保存則について解説しています。
また、これらに関係する反発係数(はねかえり係数)についても載せています。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.運動量と力積とは
力\(\vec{F}\)が働いている物体の運動方程式を考えます。
物体の質量を\(m\)とすると、運動方程式は、
\(\displaystyle{m\vec{a}=\vec{F} \cdots①}\)
ここで、加速度の定義式は、
\(\displaystyle{\vec{a}=\frac{\vec{v_{あと}}-\vec{v_{はじめ}}}{\Delta{t}}}\)
※加速度の定義についてはこちら
→変位・速度・加速度
なので、\(①\)の運動方程式は、
\(\displaystyle{\begin{eqnarray}&&m\vec{a}=\vec{F}\\\\{\Leftrightarrow}&&m・\frac{\vec{v_{あと}}-\vec{v_{はじめ}}}{\Delta{t}}=\vec{F}\end{eqnarray}}\)
と書き換えられます。
上式の両辺に\(\Delta{t}\)を掛けると
\(\displaystyle{\begin{eqnarray}&&m(\vec{v_{あと}}-\vec{v_{はじめ}})=\vec{F}・\Delta{t}\\\\{\Leftrightarrow}&&m\vec{v_{あと}}-m\vec{v_{はじめ}}=\vec{F}・\Delta{t} \cdots②\end{eqnarray}}\)
ここで、質量と速度の積\(\textcolor{red}{m・\vec{v}[kg・m/s]}\)を\(\textcolor{red}{\bf{運動量}}\)といい、力と作用時間の積\(\textcolor{red}{\vec{F}・\Delta{t}[N・s]}\)を\(\textcolor{red}{\bf{力積}}\)といいます。
\((N・s=(kg・m/s^2)・s=kg・m/s\)となり、運動量と力積の単位は同じ)
運動量と力積のどちらも、向きと大きさをもつベクトルとなります。
以上から、式\(②\)の意味は以下のようになります。
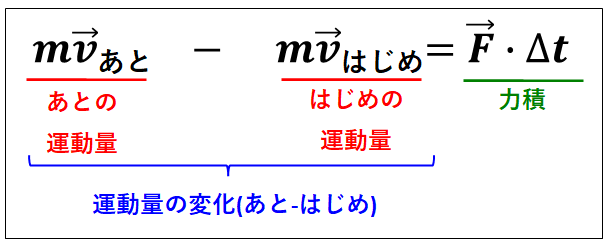
上式は、”運動量の変化は、その間に受けた物体の力積に等しい”ことを表しています。
また、\(②\)式は成分でわけて考えることもできます。
\(\displaystyle{m\vec{v_{あと}}-m\vec{v_{はじめ}}=\vec{F}\Delta{t}}\)
↓成分で考えると
\(\displaystyle{\left\{\begin{array}{l}mv_{xあと}-mv_{xはじめ}=F_x\Delta{t} (x成分)\\\\mv_{yあと}-mv_{yはじめ}=F_y\Delta{t} (y成分)\end{array}\right.}\)
2.運動量保存則
運動量保存則は、下図の状況の際に使うことができます。

運動量保存則を考えるために、例として下記のような状況を考えます。
右向きに速さ\(v_{Aはじめ}\)で運動している物体\(A\)と、右向きに速さ\(v_{Bはじめ}\)で運動している物体\(B\)が衝突することを考えます。
衝突後、\(A,B\)はそれぞれ\(v_{Aあと} ,v_{Bあと}\) の速さで右向きに運動するとします。
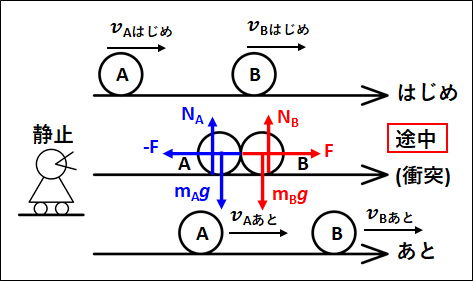
静止した人から見た\(\textcolor{red}{\bf{途中}}\)のつりあいと運動方程式を考えると、下図のようになります。
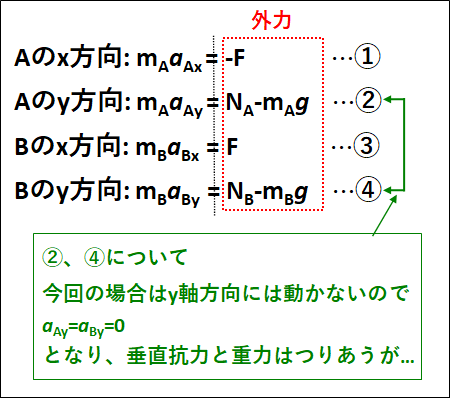
ここで、
○物体\(A,B\)の運動なので二体問題
○外力を内力化するために
の上記2つの事柄から、辺々を加えるという操作をします。
実際に、\(①+③\)から
\({m_A}{a_{Ax}}+{m_B}{a_{Bx}}=0\)
上記のように、”二体以上の運動方程式の辺々を足して外力がゼロになることを、\(\textcolor{red}{\bf{「外力が内力化された」}}\)といいます”
式変形を続けていくと、
\(\displaystyle{\begin{eqnarray}&&m_Aa_{Ax}+m_Ba_{Bx}=0\\\\{\Leftrightarrow}&&m_A\frac{v_{Aあと}-v_{Aはじめ}}{\Delta{t}}+m_B\frac{v_{Bあと}-v_{Bはじめ}}{\Delta{t}}=0\\\\{\Leftrightarrow}&&m_Av_{Aあと}+m_Bv_{Bあと}=m_Av_{Aはじめ}+m_Bv_{Bはじめ}\end{eqnarray}}\)
となります。
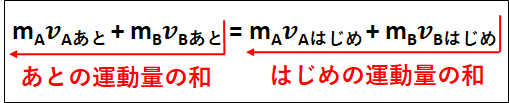
上式で表される法則を\(\textcolor{red}{\bf{運動量保存則}}\)といいます。
意味は、”複数の物体が内力を及ぼしあうだけで、外力を受けなければ(内力化できれば)これらの物体の運動量の総和は変化しない”というものになります。
今回の例では、\(x\)軸方向についてだけ運動量保存則が成り立ちますが、\(y\)軸方向についても内力化できるなら、\(y\)軸方向についても運動量保存則は成り立ちます。
\(\textcolor{red}{\bf{○ポイント}}\)
・いつ運動量保存則がつかえるのか?
→二体問題/内力化できる とき
・\(v\)は静止している人から見た値
(運動方程式は、静止した人からみて立てるから)
3.反発係数(はねかえり係数)
反発係数(はねかえり係数)\(e\)は、材質によって決まる物体同士のはねかえり度合いを表すものとなります。
反発係数\(e\)の定義は次のようになります。
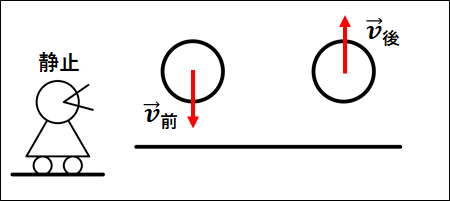
上図は、物体が地面にぶつかる前とぶつかった後の図になります。
ぶつかる前の速度を\(\vec{v}_{前}\)、ぶつかった後の速度を\(\vec{v}_{後}\)とすると、反発係数\(e\)は
\(\displaystyle{\textcolor{green}{\begin{eqnarray}&&e=\frac{|\vec{v}_{後}|}{|\vec{v}_{前}|}\\\\{\Leftrightarrow}&&|\vec{v}_{後}|=e|\vec{v}_{前}|\end{eqnarray}}}\)
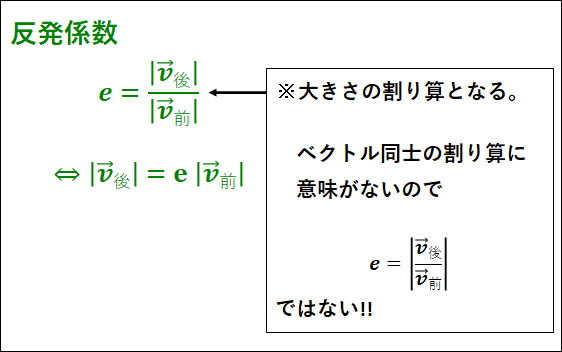
物体がなにかにぶつかると、その分エネルギーは損なわれてしまい、ぶつかる前の速さを超えることはありません。
なので、反発係数\(e\)の範囲は、
\(0{\le}e{\le}1\)
となります。
また、反発係数\(e\)の範囲が\(1\)以下であることを知っていれば、反発係数の定義において\(\vec{v}_{前}\)と\(\vec{v}_{後}\)のどちらが分母でどちらが分子か迷うことは無くなります。
基本的に\(\vec{v}_{前}\)の速さの方が大きいので、これが分子にきてしまうと\(e\)は\(1\)を超えてしまいます。
なので\(e\)が\(1\)を超えないように\(\vec{v_{前}}\)が分母で\(\vec{v_{後}}\)が分子となります。
また、速度(ベクトル)で表すと、
\(\displaystyle{\vec{v}_{後}=-\vec{v}_{前}}\)
となります。

上記が、反発係数\(e\)の定義となります。
また、反発係数はその値によって名称があります。
反発係数\(e\)の値は
\(0{\le}e{\le}1\)
となります。
(後の速さは前の速さより大きくはならない)
特に、
\(e=1\)のとき→\(\textcolor{green}{\bf{弾性衝突}}\)
\(0{\le}e{\lt}1\)のとき→\(\textcolor{green}{\bf{非弾性衝突}}\)
非弾性衝突の中でも、\(e=0\)のときを\(\textcolor{green}{\bf{完全非弾性衝突}}\)といいます。
4.二体問題における反発係数(はねかえり係数)
考える物体が一つの場合の反発係数については、記述しましたが、今回は二物体の場合の反発係数についてです。
二物体の場合には、反発係数の定義における速度を、\(\textcolor{red}{\bf{相対速度}}\)で扱います。
物体\(A\)と物体\(B\)について、ぞれぞれの前の速度を\(\vec{v}_{A前} ,\vec{v}_{B前}\) 、それぞれの後の速度を\(\vec{v}_{A後} ,\vec{v}_{B後}\) とすると、下図のようになります。
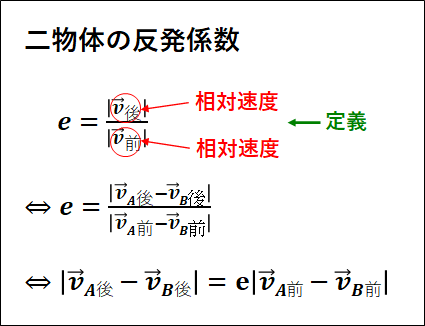
また、速度(ベクトル)で表すと、
\(\displaystyle{\vec{v}_{A後}-\vec{v}_{B後}=\textcolor{red}{-}e(\vec{v}_{A前}-\vec{v}_{B前} )}\)
となります。
5.斜め衝突
下図のように、物体が滑らかな平面に斜めに衝突する場合を考えます。
(物体と床の間の反発係数を\(e\)とする)
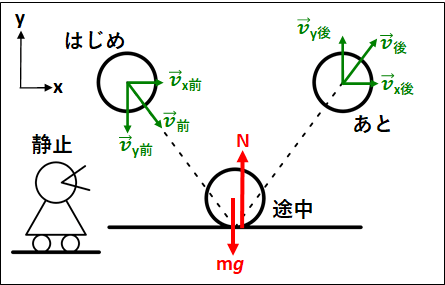
衝突前の速度を\(\vec{v}_{前}\)、衝突後の速度を\(\vec{v}_{後}\)とし、それぞれの速度は図のように\(x\)方向と\(y\)方向に分解してあります。
ここで、途中の運動方程式は、
\(\displaystyle{\begin{eqnarray}&&\left\{\begin{array}{l}ma_x=0\\ma_y=N-mg\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}m\frac{v_{x後} -v_{x前}}{\Delta{t}}=0 \cdots①\\m\frac{v_{y後} -v_{y前}}{\Delta{t}}=N-mg \cdots②\end{array}\right.\end{eqnarray}}\)
上式から、\(x\)方向の速度については\(①\)から
\(v_{x後}=v_{y前}\)
であると分かります。
しかしながら、\(y\)軸方向の速度については、\(②\)式から得られる情報はありません。
運動方程式からは\(y\)軸方向の速度がわかりませんが、反発係数を用いると、
\(\displaystyle{\begin{eqnarray}&&e=\frac{|v_{y後}|}{|v_{y前}|}\\\\{\Leftrightarrow}&&|v_{y後}|=e|v_{y前}|\\\\{\Leftrightarrow}&&v_{y後}=-ev_{y前}\end{eqnarray}}\)
となり、\(y\)軸方向の速度について情報を得ることができます。
6.衝突と力学的エネルギーの損失
反発係数の値によって、エネルギーは保存されたり失われたりします。
○弾性衝突(\(e=1\))のとき
力学的エネルギーは失われずに、保存される。
一つの物体の場合、力学的エネルギーが保存されるので、前と後の速さは同じになる。
○非弾性衝突(\(0{\le}e{\lt}1\))のとき
力学的エネルギーは減少し、失われた力学的エネルギーは熱や音、物体の変形に使われる。
一つの物体の場合、力学的エネルギーは減少してしまうので、前の速さよりも後の速さの方が小さくなる。
こちらの具体的な計算については、練習問題で扱います。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


