投稿日:
【高校物理】積分法【高校数学】【積分】
\(\require{color}\)
\(\require{cancel}\)
積分は物理において、エネルギーの計算などに用います。
今回は、積分についての基礎的な部分の解説となります。
微分・積分に関する記事は、こちらも参考にしてください
→微分係数と導関数
→様々な関数
→極限
→微分法とその応用
→積分法の応用
→よく使う積分の考え方と微積公式まとめ
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.不定積分
1-1.不定積分
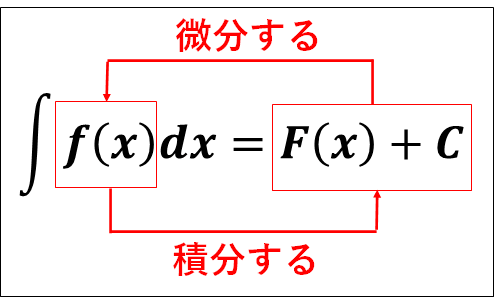
前回微分についての解説を行いましたが、微分すると\(f(x)\)になる関数を、\(f(x)\)の\(\textcolor{red}{\bf{“原始関数”}}\)といいます。
すなわち、\(F'(x)=f(x)\)のとき、\(F(x)\)は\(f(x)\)の原始関数となります。
例)
\((3x^2)’=6x\)なので、\(3x^2\)は\(6x\)の原始関数となる。
また、
\((3x^2+2)’=6x\)
\((3x^2+6)’=6x\)
となるので、\(3x^2+2\) や \(3x^2+6\) も \(6x\)の原始関数となります。
上記の例をみると、これは定数は微分すると\(0\)となることに依るものだと考えられます。
一般に、\(C\)を定数とすると\((C)’=0\)となるので、関数\(f(x)\)の1つの原始関数\(F(x)\)が分かっていれば、\(f(x)\)の任意の原始関数は
\(F(x)+C (Cは定数)\)
の形で表されます。
上式の\(C\)を\(\textcolor{red}{\bf{積分定数}}\)といいます。
また、この表示を\(f(x)\)の\(\textcolor{red}{\bf{“不定積分”}}\)といい、
\(\displaystyle{\int{f(x)}dx}\)
で表します。
\(\int\)はインテグラルといいます。
以上から、関数\(f(x)\)の不定積分について
\(F'(x)=f(x)\)のとき
\(\displaystyle{\int{f(x)}dx=F(x)+C (Cは積分定数)}\)
となります。
今後、\(C\)は積分定数であるとします。
\(\textcolor{red}{\bf{関数}}\)\(\textcolor{red}{f(x)}\)\(\textcolor{red}{\bf{の不定積分を求めることを、}}\)\(\textcolor{red}{f(x)}\)\(\textcolor{red}{\bf{を積分する}}\)といいます。
また、積分することと微分することは、互いに逆の計算であるといえます。
1-2.\(x^n\)の不定積分
微分の解説で扱った、\(x^n\)について、
\((x^n)’=nx^{n-1}\)
なので、\(x^n\)の不定積分は
\(\displaystyle{\int{x^n}dx=\frac{1}{n+1}x^{n+1}+C}\)
となります。
確認のために、\(\displaystyle{\frac{1}{n+1}x^{n+1}+C}\)を微分してみると、
\(\displaystyle{\begin{eqnarray}\left(\frac{1}{n+1}x^{n+1}+C\right)’&=&\frac{1}{n+1}・(n+1)x^{n+1-1}+0\\\\&=&x^n\end{eqnarray}}\)
となり、\(x^n\)の原始関数は\(\displaystyle{\frac{1}{n+1}x^{n+1}+C}\)であることが確認できます。
1-3.定数倍・和・差の不定積分
“5-1.微分係数と導関数“で解説したように、定数倍・和・差の微分は以下のようになります。
\(F'(x)=f(x)\)、\(G'(x)=g(x)\)のとき
\(\underline{\bf{定数倍の微分}}\)
\(\{kF(x)\}’=kf(x)\)
\(\underline{\bf{和の微分}}\)
\(\{F(x)+G(x)\}’=f(x)+g(x)\)
\(\underline{\bf{差の微分}}\)
\(\{F(x)-G(x)\}’=f(x)-g(x)\)
上記から、
\(kF(x)\) は \(kf(x)\) の原始関数の一つ
\(F(x)+G(x)\) は \(f(x)+g(x)\) の原始関数の一つ
\(F(x)-G(x)\) は \(f(x)-g(x)\) の原始関数の一つ
となるので、積分定数を考えると定数倍・和・差の不定積分に関して、以下の式が成り立ちます。
\(\underline{\bf{定数倍の不定積分}}\)
\(\displaystyle{\int{kf(x)}dx=kF(x)+C kは定数 \cdots①}\)
また、\(\int{kf(x)}dx=k\int{f(x)}dx\)のように、定数部分をインテグラルの前に出すこともできます。
\(\underline{\bf{和の不定積分}}\)
\(\displaystyle{\int{\{f(x)+g(x)\}}dx=F(x)+G(x)+C \cdots②}\)
\(\underline{\bf{差の不定積分}}\)
\(\displaystyle{\int{\{f(x)-g(x)\}}dx=F(x)-G(x)+C \cdots③}\)
下記にこれらの計算例を載せておきます。
\(\underline{\bf{①の計算例}}\)
\(\displaystyle{\begin{eqnarray}\int{2x^2}dx&=&2\int{x^2}dx\\\\&=&2(\frac{1}{3}x^3)+C\\\\&=&\frac{2}{3}x^3+C\end{eqnarray}}\)
\(\underline{\bf{②の計算例}}\)
\(\displaystyle{\begin{eqnarray}\int{(x^2+x)}dx&=&\int{x^2}dx+\int{x}dx\\\\&=&\frac{1}{3}x^3+\frac{1}{2}x^2+C\end{eqnarray}}\)
\(\underline{\bf{③の計算例}}\)
\(\displaystyle{\begin{eqnarray}\int{(x^2-x)}dx&=&\int{x^2}dx-\int{x}dx\\\\&=&\frac{1}{3}x^3-\frac{1}{2}x^2+C\end{eqnarray}}\)
1-4.様々な関数の不定積分
変数が\(x\)でない関数についても、同様に不定積分を考えてみます。
変数が\(t\)のものについて考えてみますが、こちらも変数が\(x\)から\(t\)に変わっただけで、計算自体は同様に行います。
下記に計算例を載せておきます。
例) \(t\)の関数について
\(\displaystyle{\int{1}dt=t+C}\)
\(\displaystyle{\int{t}dt=\frac{1}{2}t^2+C}\)
\(\displaystyle{\int{t^2}dt=\frac{1}{3}t^3+C}\)
また、積分定数\(C\)は、与えられた条件によっては定まります。
例えば、\(f(x)=x^2\)として、原始関数の1つを\(F(x)\)とすると、
\(\displaystyle{\begin{eqnarray}F(x)&=&\int{f(x)}dx\\\\&=&\int{x^2}dx\\\\&=&\frac{1}{3}x^3+C\end{eqnarray}}\)
よって、
\(\displaystyle{F(x)=\frac{1}{3}x^3+C}\)
ここで、\(F(0)=3\)という条件が与えられたとき、
\(\displaystyle{\begin{eqnarray}&&F(0)=\frac{1}{3}・0^2+C\\\\\Leftrightarrow&&C=3\end{eqnarray}}\)
より、\(C=3\)と定まります。
従って、原始関数は
\(\displaystyle{F(x)=\frac{1}{3}x^3+3}\)
となります。
2.定積分
2-1.定積分
関数\(f(x)\)の原始関数の1つを\(F(x)\)とし、\(a\)、\(b\)を\(f(x)\)の定義域内の任意の値とするとき、\(F(b)-F(a)\)は、\(F(x)\)の選び方とは無関係に\(a\)、\(b\)の値だけで定まります。
※\(f(x)=x\)とすると、\(\displaystyle{F(x)=\int{x}dx=\frac{1}{2}x^2+C}\)となる。
このとき
\(\displaystyle{\begin{eqnarray}F(b)-F(a)&=&\left(\frac{1}{2}b^2+C\right)-\left(\frac{1}{2}a^2+C\right)\\\\&=&\frac{1}{2}b^2-\frac{1}{2}a^2\end{eqnarray}}\)
となり、定数\(C\)とは無関係に\(a\)と\(b\)の値だけで決まる。
\(\textcolor{red}{\bf{この}}\)\(\textcolor{red}{F(b)-F(a)}\)\(\textcolor{red}{\bf{を}}\)\(\displaystyle{\textcolor{red}{\int_a^b{f(x)}dx}}\)\(\textcolor{red}{\bf{と書き、これを}}\)\(\textcolor{red}{f(x)}\)\(\textcolor{red}{\bf{の}}\)\(\textcolor{red}{a}\)\(\textcolor{red}{\bf{から}}\)\(\textcolor{red}{b}\)\(\textcolor{red}{\bf{までの”定積分”}}\)といいます。
このとき、\(a\)を下端、\(b\)を上端といいます。
また、\(F(b)-F(a)\)を\(\left[F(x)\right]_a^b\)とも書きます。
以上から、以下のように書くことができます。
☆\(F'(x)=f(x)\)のとき
\(\displaystyle{\begin{eqnarray}\int_a^b{f(x)}dx&=&\left[F(x)\right]_a^b\\\\&=&F(b)-F(a)\end{eqnarray}}\)
以下に例を載せておきます。
例)
\(\displaystyle{\begin{eqnarray}\int_1^2{x}dx&=&\left[\frac{1}{2}x^2\right]_1^2\\\\&=&\frac{1}{2}・2^2-\frac{1}{2}・1^2\\\\&=&\frac{3}{2}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\int_2^1{x}dx&=&\left[\frac{1}{2}x^2\right]_2^1\\\\&=&\frac{1}{2}・1^2-\frac{1}{2}・2^2\\\\&=&-\frac{3}{2}\end{eqnarray}}\)
\(\displaystyle{\begin{eqnarray}\int_2^2{x}dx&=&\left[\frac{1}{2}x^2\right]_2^2\\\\&=&\frac{1}{2}・2^2-\frac{1}{2}・2^2\\\\&=&0\end{eqnarray}}\)
2-2.定積分の性質
\(\underline{\bf{定数倍・和・差の定積分}}\)
定積分についても不定積分と同様に、定数倍・和・差について以下の式が成り立ちます。
\(\underline{\bf{定数倍の定積分}}\)
\(\displaystyle{\int_a^b{kf(x)}dx=k\int_a^b{f(x)}dx kは定数}\)
\(\underline{\bf{和の定積分}}\)
\(\displaystyle{\int_a^b{\{f(x)+g(x)\}}dx=\int_a^b{f(x)}dx+\int_a^b{g(x)}dx}\)
\(\underline{\bf{差の定積分}}\)
\(\displaystyle{\int_a^b{\{f(x)-g(x)\}}dx=\int_a^b{f(x)}dx-\int_a^b{g(x)}dx}\)
以下に計算例を載せておきます。
例)
\(\underline{\bf{定数倍の定積分計算例}}\)
\(\displaystyle{\begin{eqnarray}\int_1^2{3x}dx&=&3\int_1^2{x}dx\\\\&=&3\left[\frac{1}{2}x^2\right]_1^2\\\\&=&\frac{3}{2}\left[2^2-1^2\right]\\\\&=&\frac{9}{2}\end{eqnarray}}\)
\(\underline{\bf{和の定積分計算例}}\)
\(\displaystyle{\begin{eqnarray}\int_1^2{(x^2+x)}dx&=&\int_1^2{x^2}dx+\int_1^2{x}dx\\\\&=&\left[\frac{1}{3}x^3\right]_1^2+\left[\frac{1}{2}x^2\right]_1^2\\\\&=&\frac{1}{3}(2^3-1^3)+\frac{1}{2}(2^2-1^2)\\\\&=&\frac{1}{3}(8-1)+\frac{1}{2}(4-1)\\\\&=&\frac{7}{3}+\frac{3}{2}\\\\&=&\frac{14+9}{6}\\\\&=&\frac{23}{6}\end{eqnarray}}\)
\(\underline{\bf{差の定積分計算例}}\)
\(\displaystyle{\begin{eqnarray}\int_1^2(x^2-x)dx&=&\int_1^2{x^2}dx-\int_1^2{x}dx\\\\&=&\left[\frac{1}{3}x^3\right]_1^2-\left[\frac{1}{2}x^2\right]_1^2\\\\&=&\frac{1}{3}(8-1)-\frac{1}{2}(4-1)\\\\&=&\frac{7}{3}-\frac{3}{2}\\\\&=&\frac{14-9}{6}\\\\&=&\frac{5}{6}\end{eqnarray}}\)
\(\underline{\bf{定積分の性質}}\)
定積分の性質には、以下のようなものがあります。
\(\displaystyle{\int_a^a{f(x)}dx=0 \cdots①}\)
\(\displaystyle{\int_b^a{f(x)}dx=-\int_a^b{f(x)}dx \cdots②}\)
\(\displaystyle{\int_a^b{f(x)}dx=\int_a^c{f(x)}dx+\int_c^b{f(x)}dx \cdots③}\)
以下に証明を載せておきます。
\(\underline{\bf{①について}}\)
\(F'(x)=f(x)\)とすると
\(\displaystyle{\begin{eqnarray}\int_a^a{f(x)}dx&=&\left[F(x)\right]_a^a\\\\&=&F(a)-F(a)\\\\&=&0\end{eqnarray}}\)
\(\underline{\bf{②について}}\)
\(F'(x)=f(x)\)とすると
\(\displaystyle{\begin{eqnarray}\int_b^a{f(x)}dx&=&\left[F(x)\right]_b^a\\\\&=&F(a)-F(b)\\\\&=&-\{F(b)-F(a)\}\\\\&=&-\int_a^b{f(x)}dx\end{eqnarray}}\)
\(\underline{\bf{③について}}\)
\(F'(x)=f(x)\)とすると
\(\displaystyle{\begin{eqnarray}&&\int_a^c{f(x)}dx+\int_c^b{f(x)}dx\\\\&&=\left[F(x)\right]_a^c+\left[F(x)\right]_c^b\\\\&&=\{F(c)-F(a)\}+\{F(b)-F(c)\}\\\\&&=F(b)-F(a)\\\\&&=\int_a^b{f(x)}dx\end{eqnarray}}\)
となります。
2-3.\(f(t)\)の定積分
こちらも不定積分のときと同様に、変数が\(x\)から\(t\)へと変わっただけで、計算自体は同様となります。
\(t\)を変数とする関数の定積分は次のようになります。
\(F'(t)=f(t)\)のとき、
\(\displaystyle{\begin{eqnarray}\int_a^b{f(t)}dt&=&\left[F(t)\right]_a^b\\\\&=&F(b)-F(a)\end{eqnarray}}\)
上記式から、計算結果は変数に関わらずに\(a\)と\(b\)で決まることが分かります。
すなわち、
\(\displaystyle{\begin{eqnarray}\int_a^b{f(t)}dt&=&\int_a^b{f(x)}dx\\\\&=&F(b)-F(a)\end{eqnarray}}\)
となり、定積分の値は変数が異なっても同じとなります。
また、関数\(f(t)\)に対して、\(F'(t)=f(t)\)のとき、\(f(t)\)の定積分
\(\displaystyle{\int_a^x{f(t)}dt=F(x)-F(a)}\)
は\(x\)の関数となります。
この関数の右辺を\(x\)で微分すると、
\(\displaystyle{\begin{eqnarray}\{F(x)-F(a)\}’&=&F'(x)-\{F(a)\}’\\\\&=&f(x)\end{eqnarray}}\)
となるので、次のことが成り立ちます。
(※上式の\(F(a)\)は定数なので、微分すると\(0\)となる)
上式から\(a\)を定数とするとき、\(x\)の関数
\(\displaystyle{\int_a^x{f(t)}dt}\)
の導関数は、
\(\displaystyle{f(x)}\)
となります。
\((※\int_a^x{f(t)}dt{\bf{を}}x{\bf{で微分すると}}f(x){\bf{となる}})\)
すなわち、
\(\displaystyle{\frac{d}{dx}\int_a^x{f(t)}dt=f(x)}\)
が成り立ちます。
3.図形の面積と定積分
3-1.面積と定積分の関係
図形の面積と定積分との関係を考えるために、具体的な関数で調べていきます。
\(\underline{\bf{具体例①}}\)
一次関数\(y=x+1\)のグラフと、\(x\)軸および\(y\)軸と\(x=t\)で囲まれた部分の面積を調べます。
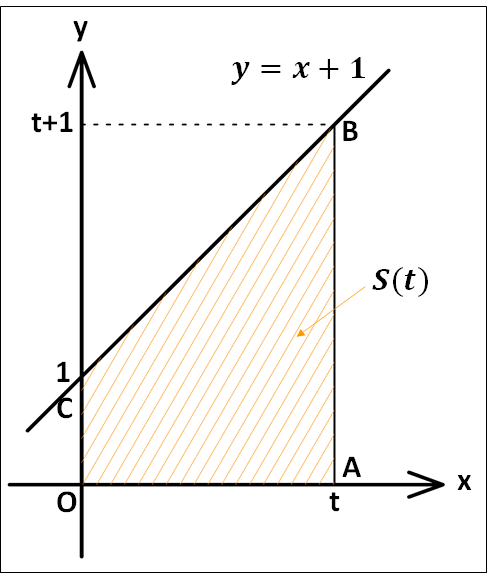
上図において、斜線部\(OABC\)の面積は\(t\)の関数であり、この面積を\(S(t)\)とすると、台形の面積を求める式から
\(\displaystyle{\begin{eqnarray}S(t)&=&\frac{1}{2}{1+(t+1)×t}\\\\&=&\frac{1}{2}(t+2)×t\\\\&=&\frac{1}{2}t^2+t\end{eqnarray}}\)
また、この\(S(t)\)を\(t\)で微分すると
\(\displaystyle{\begin{eqnarray}S'(t)&=&\left(\frac{1}{2}t^2+t\right)’\\\\&=&t+1\end{eqnarray}}\)
ここで、\(S'(t)\)の変数を\(x\)に変更すると
\(S'(x)=x+1\)
以上の結果から、
\(f(x)=x+1\)
\(S'(x)=x+1\)
なので
\(S'(x)=f(x)\)
となります。
次に、\(y=x+1\)のグラフと\(x\)軸および\(x=a\) , \(x=b\)で囲まれた部分の面積を調べてみます。
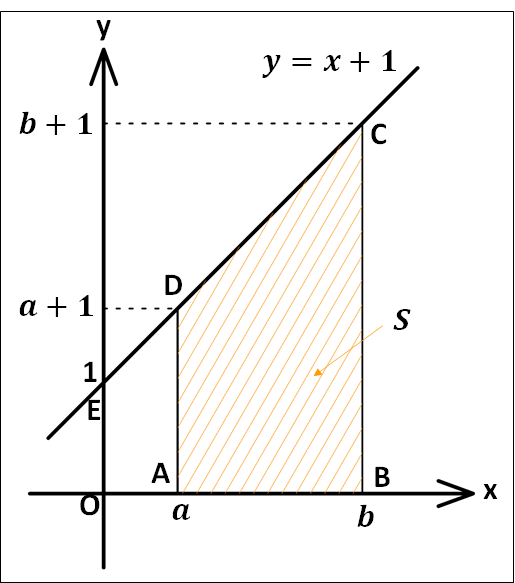
上図において、\(ABCD\)の面積を\(S\)とすると、この面積は\(S(t)\)を用いて
\(S=\textcolor{blue}{S(b)}-\textcolor{red}{S(a)}\)
と表せます。
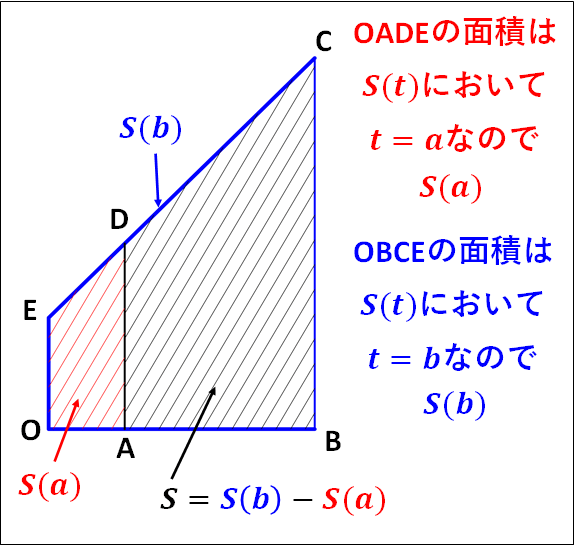
また先ほどの結果から、\(S'(x)=f(x)\)であるのでこの面積は、
\(\displaystyle{\begin{eqnarray}S&=&\textcolor{blue}{S(b)}-\textcolor{red}{S(a)}\\\\&=&\left[S(x)\right]_a^b\\\\&=&\int_a^b{S'(x)}dx\\\\&=&\int_a^b{f(x)}dx\end{eqnarray}}\)
と表せます。
\(\underline{\bf{具体例②}}\)
次に、定積分と面積の関係を2次関数\(y=x^2\)で考えてみます。
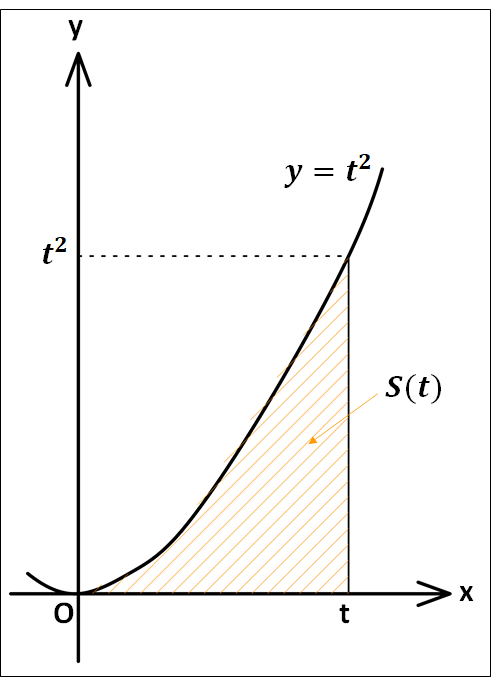
上図斜線部の面積は\(t\)の関数であり、これを\(S(t)\)とします。
このとき、\(S'(t)=t^2\)であれば、具体例\(①\)の\(y=x+1\)のときと同様にして、面積を積分の形で表せます。
そのために、次の図を考えます。
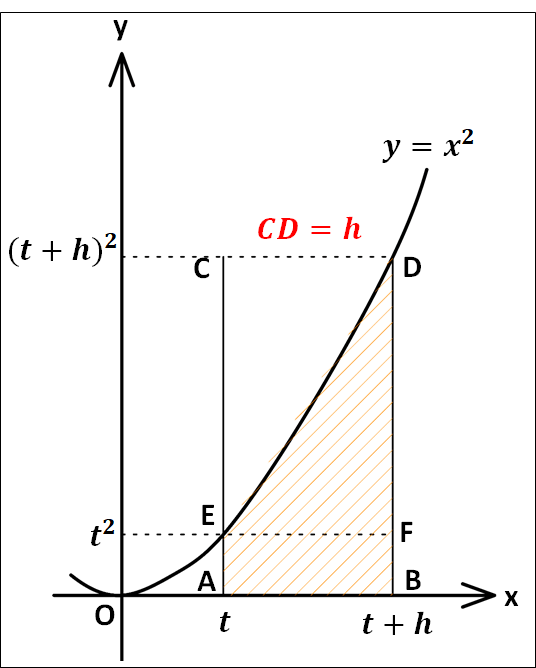
上図において、
\(\displaystyle{\begin{eqnarray}CD&=&EF\\&=&AB\\\\&=&(t+h)-t\\\\&=&h\end{eqnarray}}\)
となっています。
今、\(y=x^2\)と\(x\)軸、\(x=t\)で囲まれた部分の面積を\(S(t)\)としているので、上図斜線部の面積は\(h\gt0\)とすると、具体例\(①\)と同様に考えて
\(\displaystyle{S(t+h)-S(t)}\)
となります。
これと、横の長さが\(h\)である2つの長方形\(ABFE\)と\(ABDC\)の面積の大小関係を考えます。
長方形\(ABFE\)の面積は\(ht^2\)
長方形\(ABDC\)の面積は\(h(t+h)^2\)
であり、図から大小関係は
\(\displaystyle{ht^2{\lt}S(t+h)-S(t){\lt}h(t+h)^2}\)
となります。
この不等式をそれぞれ\(h\)で割ると、\(h\gt0\)なので、
\(\displaystyle{t^2\lt{\frac{S(t+h)-S(t)}{h}}{\lt}{(t+h)^2}}\)
となります。
\(h\lt0\)のときには斜線部の面積は
\(\displaystyle{S(t)-S(t+h)}\)
また長方形の大小関係は
\(\displaystyle{h(t+H)^2{\lt}S(t)-S(t+h){\lt}ht^2}\)
これをそれぞれ\(h\)で割りますが、\(h\lt0\)であることに気を付けると
\(\displaystyle{t^2\lt\frac{S(t+h)-S(t)}{h}\lt(t+h)^2}\)
となり、結果は\(h\gt0\)の場合と同様になります。
また、
\(\displaystyle{\lim_{h\to0}(t+h)^2=t^2}\)
となります。
以上のことから、\(h\to0\)とすると
\(\displaystyle{t^2\lt\frac{S(t+h)-S(t)}{h}{\lt}t^2}\)
となるので
\(\displaystyle{\lim_{h\to0}\frac{S(t+h)-S(t)}{h}=t^2}\)
となります。
上式右辺は微分の定義となるので
\(\displaystyle{S'(t)=t^2}\)
です。
ここで、\(y=x^2\)のグラフと\(x\)軸および2直線\(x=a\) , \(x=b\)で囲まれた部分の面積を\(S\)とすると\(S\)は\(S(t)\)を用いて
\(\displaystyle{S=S(b)-S(a)}\)
と表されます。
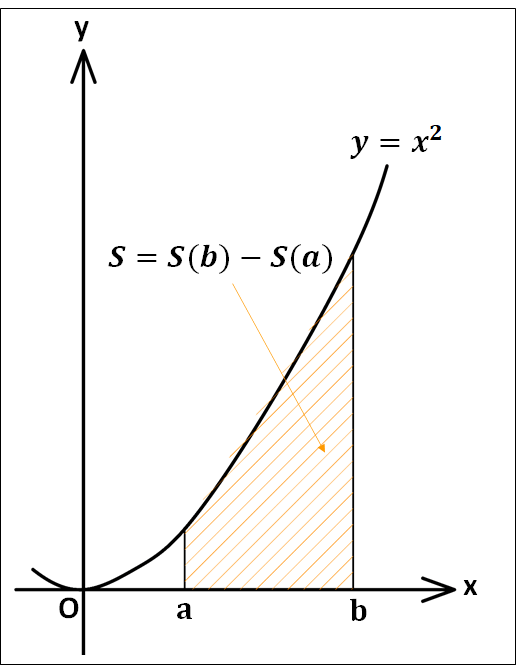
以上より、定積分の定義と性質から
\(\displaystyle{\begin{eqnarray}S&=&S(b)-S(a)\\\\&=&\left[S(t)\right]_a^b\\\\&=&\int_a^b{S'(t)}dt\\\\&=&\int_a^b{t^2}dt\\\\&=&\int_a^b{x^2}dx\end{eqnarray}}\)
が成り立ちます。
一般に関数\(y=f(x)\)について、次のことが成り立ちます。
\(a\le{x}\le{b}\)の範囲で\(f(x)\ge0\)のとき、\(y=f(x)\)のグラフと\(x\)軸および2直線\(x=a\)、\(x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{\textcolor{red}{S=\int_a^b{f(x)}dx}}\)
となります。
例)
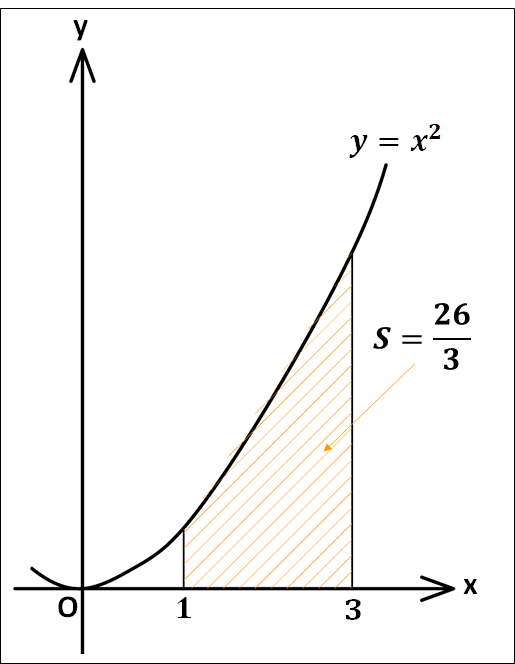
\(y=x^2\)と\(x\)軸および\(x=1\)、\(x=3\)で囲まれた部分の面積\(S\)は
\(\displaystyle{\begin{eqnarray}S&=&\int_1^3{x^2}dx\\\\&=&\left[\frac{1}{3}x^3\right]_1^3\\\\&=&\frac{1}{3}(3^3-1^3)\\\\&=&\frac{1}{3}(27-1)\\\\&=&\frac{26}{3}\end{eqnarray}}\)
また、次のことも成り立ちます。
\(a\le{x}\le{b}\)の範囲で\(f(x)\le0\)のとき、\(y=f(x)\)のグラフと\(x\)軸および2直線\(x=a\)、\(x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{\textcolor{red}{S=\int_a^b{\{-f(x)}\}dx}}\)
(※\(x\)軸より下側は負の面積となる)
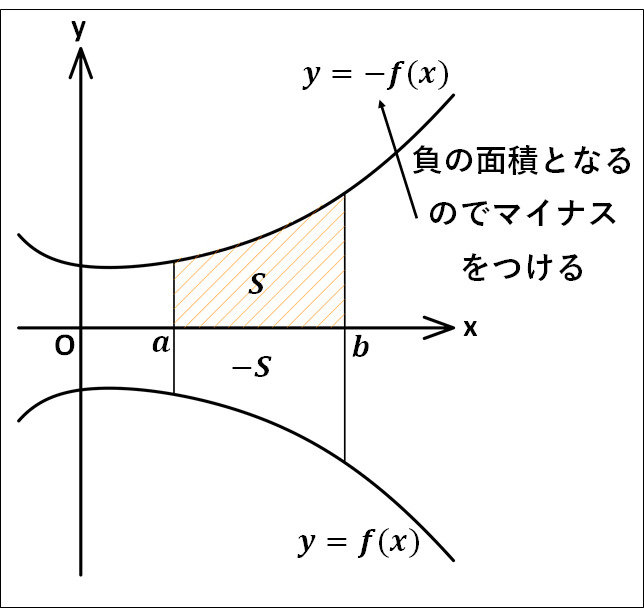
例)
\(y=-x^2\)と\(x\)軸および\(x=1\)、\(x=3\)で囲まれた部分の面積\(S\)は、
\(\displaystyle{\begin{eqnarray}S&=&\int_1^3{-f(x)}dx\\\\&=&\int_1^3{{-(-x^2)}}dx\\\\&=&\int_1^3{x^2}dx\\\\&=&\left[\frac{1}{3}x^3\right]_1^3\\\\&=&\frac{1}{3}(27-1)\\\\&=&\frac{26}{3}\end{eqnarray}}\)
となります。
3-2.2つの曲線の間の面積
2つの関数\(f(x)\)、\(g(x)\)が\(a{\le}x{\le}b\)の範囲で\(f(x){\ge}g(x)\)のとき、\(y=f(x)\)のグラフと\(y=g(x)\)のグラフの間の部分の面積を考えます。
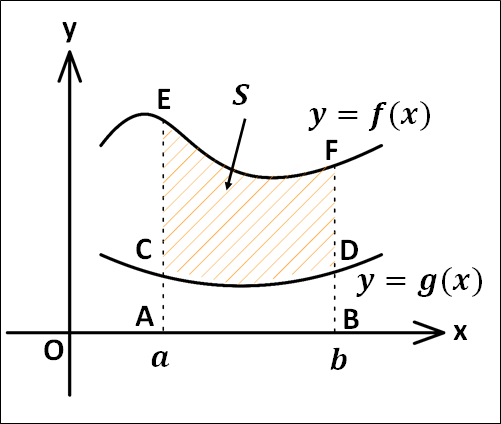
上図斜線部の面積\(S\)は\(AEFB\)から\(ACDB\)を引いたものとなります。
\(AEFB\)部分の面積は、
\(\displaystyle{\int_a^b{f(x)}dx}\)
\(ACDB\)部分の面積は、
\(\displaystyle{\int_a^b{g(x)}dx}\)
なので、斜線部面積\(S\)は、 \(AEFB\) の面積から \(ACDB\) の面積を引いた
\(\displaystyle{\begin{eqnarray}S&=&\int_a^b{f(x)}dx-\int_a^b{g(x)}dx\\\\&=&\int_a^b{\{f(x)-g(x)\}}dx\end{eqnarray}}\)
で表されます。
次に、斜線部分全体が\(x\)軸の上側にないときを考えます。
2つのグラフを\(y\)軸方向に同じだけ移動させても、斜線部面積は変わらないので、斜線部全体が\(x\)軸の上側にくるように\(y\)軸の正の方向に\(k\)だけ移動させると下図のようになります。
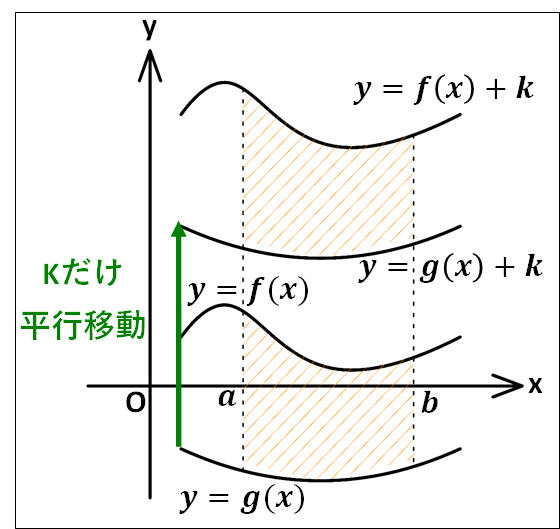
このときの斜線部の面積\(S\)は、
\(\displaystyle{\begin{eqnarray}S&=&\int_a^b{\{f(x)+k\}}dx-\int_a^b{\{g(x)+k\}}dx\\\\&=&\int_a^b{\{f(x)-g(x)+k-k\}}dx\\\\&=&\int_a^b{\{f(x)-g(x)\}}dx\end{eqnarray}}\)
となります。
以上のことから、
\(a{\le}x{\le}b\)の範囲で、\(f(x){\ge}g(x)\)のとき\(y=f(x)\)と\(y=g(x)\)および2直線\(x=a\)、\(x=b\)で囲まれた部分の面積\(S\)は、グラフが\(x\)軸の上側にある場合でも下側にある場合でも、
\(\displaystyle{\textcolor{red}{S=\int_a^b{\{f(x)-g(x)\}}dx}}\)
と表せます。
例)
\(y=x^2-4\)と直線\(y=x+2\)で囲まれた部分の面積を求めてみます。
\(y=x^2-4\)と\(y=x+2\)の交点は、
\(\displaystyle{\begin{eqnarray}&&x^2-4=x+2\\\\\Leftrightarrow&&x^2-x-6=0\\\\\Leftrightarrow&&(x-3)(x+2)=0\end{eqnarray}}\)
より、\(x=-2 , 3\)
よって、グラフの概形は次のようになります。
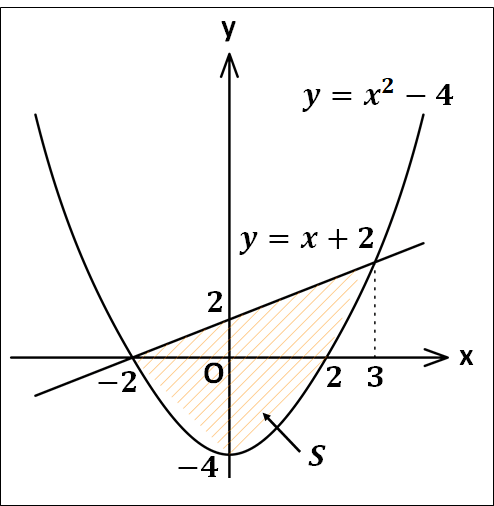
よって、求める面積を\(S\)とすると、
\(\displaystyle{\begin{eqnarray}S&=&\int_{-2}^3{\{x+2-(x^2-4)\}}dx\\\\&=&\int_{-2}^3\{-x^2+x+6\}dx\\\\&=&=\left[-\frac{1}{3}x^3+\frac{1}{2}x^2+6x\right]_{-2}^3\\\\&=&\left(-9+\frac{9}{2}+18\right)-\left(\frac{8}{3}+2-12\right)\\\\&=&\left(9+\frac{9}{2}\right)-\left(\frac{8}{3}-10\right)\\\\&=&19+\frac{27-16}{6}\\\\&=&\frac{114+11}{6}\\\\&=&\frac{125}{6}\end{eqnarray}}\)
となります。
今回は以上となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


