投稿日:
【高校物理】落下運動②【落下運動】
\(\require{color}\)
\(\require{cancel}\)
落下運動①では、直線上を運動する物体を扱いましたが、この記事では平面上を運動する物体を扱います。
運動する物体の扱いになるので、運動方程式を用いますが、今回は平面上を運動物体ですので\(x\)軸方向と\(y\)軸方向に関する運動方程式を立式します。
また、立式した運動方程式から\(v-t\)グラフを描きますが、こちらも\(x\)軸方向と\(y\)軸方向それぞれのグラフを描きます。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.落下運動について
落下運動①でみた自由落下や鉛直投げ上げなどは、1つの軸上(\(y\)軸上)での運動でした。
ここからは、\(x-y\)平面上での落下運動をみていくことにします。
(→落下運動①)
今回扱うのは、”水平投射”と”斜方投射”になります。
また、運動方程式を扱うので、こちらも参考にしてください。
→運動の3法則と束縛条件
2.水平投射
“水平投射”とは、物体を真横(水平方向)に投げた際の運動になります。
例を考えていきます。
質量\(m\)の物体を、ビルの上から右向きに初速度\(v_0\)で投げ出すことを考えます。
投げた物体は、右斜め下方向に運動するので、\(x\)軸を右向き正、\(y\)軸を下向き正として設定します。
原点は、物体が運動をはじめる直前(投げ出される直前)である、人の手を離れる瞬間を原点とします。
状況としては、下図のようになります。
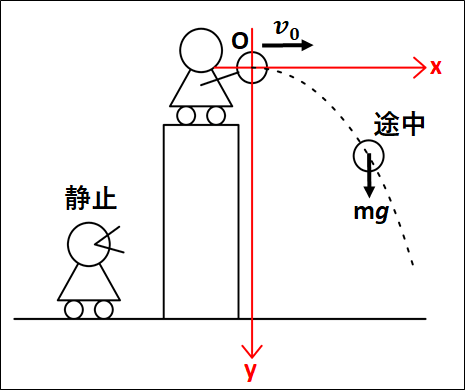
物体が運動している途中でかかっている力は、重力が鉛直下向きにはたらいています。
このことから、それぞれの軸方向にはたらいている力は、
\(x\)軸方向
→はたらいている力なし
\(y\)軸方向
→重力
となります。
重力は、\(y\)軸の正の方向にはたらいているので、\(+mg\)となります。
以上のことから、力の符合に注意して\(x\)軸方向と\(y\)軸方向に関して運動方程式を立てます。
\(x\)軸方向の加速度を\(a_x\)、\(y\)軸方向の加速度を\(a_y\)とすると、運動方程式は
\(\displaystyle{\begin{eqnarray}&&\left\{\begin{array}{l}ma_x=0 (x軸方向)\\ma_y=mg (y軸方向)\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{c}a_x=0 \textcolor{green}{(v_x-t{\bf{グラフの傾き}})}\\a_y=g \textcolor{green}{(v_y-t{\bf{グラフの傾き}})}\end{array}\right.\end{eqnarray}}\)
上式より、運動方程式が加速度について解けたので、\(x\)軸方向と\(y\)軸方向について\(v-t\)グラフを描いていきます。
その際、分かりやすいように縦に並べて描きます。
\(x\)軸方向のグラフを\(v_x-t\)グラフ、\(y\)軸方向のグラフを\(v_y-t\)グラフとします。
\(x\)軸方向の初速度を\(v_{xはじめ}\) とすると、はじめ\(x\)軸の正方向に\(v_0\)で投げたので、
\(v_{xはじめ} =v_0\)
また、運動方程式を解いた結果から
\(a_x=0\)
なので、グラフの傾きは\(0\)(\(x\)軸と平行)になります。
\(y\)軸方向の初速度を\(v_{yはじめ}\) とすると、はじめ\(y\)軸方向には速度を加えていません。
よって、
\(v_{yはじめ} =0\)
また、運動方程式を解いた結果から
\(a_y=g\)
なので、グラフの傾きは\(+g\)(右上がり)となります。
以上のことから、それぞれの\(v-t\)グラフを縦に並べて描くと下図のようになります。
\(v-t\)グラフは\(t_{あと}\)秒後までを描いています。
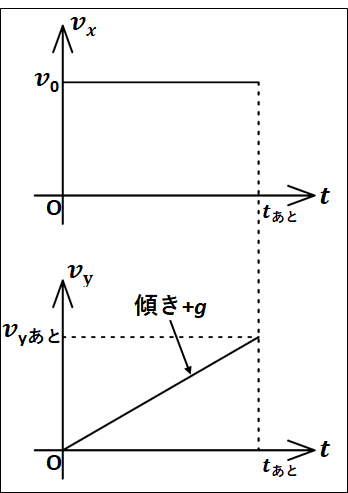
時間軸は、\(x\)方向の物体の運動と\(y\)軸方向の物体の運動とで共有しています。
ここからは覚える必要はありませんが…
○時刻\(t_{あと}\)における\(x\)軸方向の速度\(v_{xあと}\)
\(v_x-t\)グラフから、\(x\)軸方向の速度は常に一定の値\(v_0\)なので、
\(v_{xあと}=v_0\)
○時刻\(t_{あと}\)における\(y\)軸方向の速度\(v_{yあと}\)
\(v_y-t\)グラフにおける、加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&g=\frac{v_{yあと}-0}{t_{あと}-0}\\\\\Leftrightarrow&&v_{yあと}=gt_{あと}\end{eqnarray}}\)
○時刻\(t_{あと}\)における\(x\)軸方向の物体の位置\(x\)
\(v_x-t\)グラフの面積から
\(\displaystyle{x=v_0t_{あと}}\)
○時刻\(t_{あと}\)における\(y\)軸方向の物体の位置\(y\)
\(v_y-t\)グラフの面積から
\(\displaystyle{\begin{eqnarray}y&=&\frac{1}{2}v_{yあと} t_{あと}\\\\&=&\frac{1}{2}gt_{あと}^2 (∵v_{yあと}=gt_{あと})\end{eqnarray}}\)
以上のように、様々なことを求めることができます。
また問題文中で、\(x\)軸か\(y\)軸のどちらかのみの情報しか与えられていない場合でも、\(v_x-t\)グラフと\(v_y-t\)グラフの時間軸は共有しているので、時間の値を介してもう片方の情報を求めることができます。
3.斜方投射
“斜方投射”とは、物体を斜め上に投げた際の運動になります。
こちらも例を考えていきます。
下図のように、水平方向と角度\(\theta\)をなす方向に、初速度\(v_0\)で投げ出した質量\(m\)の物体を考えます。
物体は投げ出されたあと、斜め右上方向に運動するので\(x\)軸の正を右方向、\(y\)軸の正を上方向にとります。
原点は、物体が投げ出される直前のところにとっています。
物体が運動している途中では、鉛直下向きに重力\(mg\)がかかっています。
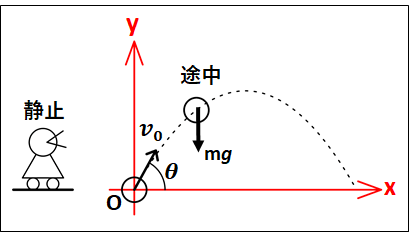
次に、\(x\)軸方向と\(y\)軸方向についての初速度を求めていきます。
物体は\(x\)軸と角度\(\theta\)をなす斜め方向に\(v_0\)で投げ出されているので、この初速度の\(x\)成分と\(y\)成分を考えます。
その際に直角三角形を考え、三角関数を用いて初速度\(v_0\)を\(x\)軸方向と\(y\)軸方向に分解します。
力(ベクトル)の分解にやベクトルの成分表示については、こちらを参考にしてください
→三角関数の定義と関係式
→力とベクトル
→練習問題1(三角関数の定義とグラフ)
→練習問題(ベクトル)
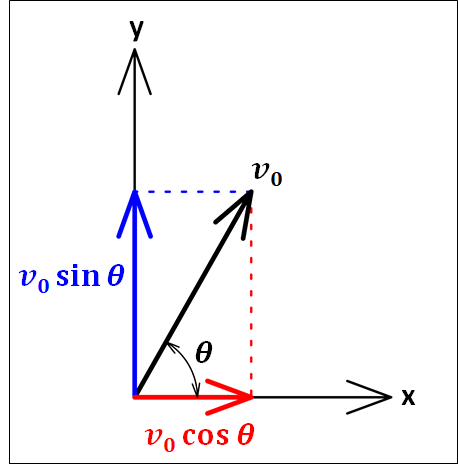
\(x\)軸方向と\(y\)軸方向の初速度を、それぞれ\(v_{xはじめ}\) 、\(v_{yはじめ}\) とします。
初速度を分解すると、\(x\)軸方向の成分に関しては\(\theta\)にへばりついている辺なので
\({\bf{斜辺}}×\cos\theta\)
となります。
実際に計算すると
\(v_{xはじめ} =v_0\cos\theta\)
また、\(y\)軸方向の成分に関しては、\(\theta\)の向かい側の辺になるので
\({\bf{斜辺}}×\sin\theta\)
となります。
実際に計算すると、
\(v_{yはじめ} =v_0\sin\theta\)
以上から、\(x\)軸方向と\(y\)軸方向の初速度が分かりました。
次は、物体は運動しているので運動方程式を立てます。
注意する点としては、物体にかかっている力は重力\(mg\)のみで、これは鉛直下向きにかかっています。
今、\(y\)軸は上向きを正としているので、重力は\(-mg\)となります。
これに注意して、水平投射のときと同様に\(x\)軸方向と\(y\)軸方向について運動方程式を立てると、
\(\displaystyle{\begin{eqnarray}&&\left\{\begin{array}{l}ma_x=0\\ma_y=-mg\end{array}\right.\\\\{\Leftrightarrow}&&\left\{\begin{array}{l}a_x=0\\a_y=-g\end{array}\right.\end{eqnarray}}\)
運動方程式を加速度について解いたことで、それぞれの方向に関する\(v-t\)グラフの傾きが分かりました。
以上のことから、それぞれの\(v-t\)グラフを描くと、以下のようになります。
\(v-t\)グラフは、\(t_{あと}\)秒後までを描いています。
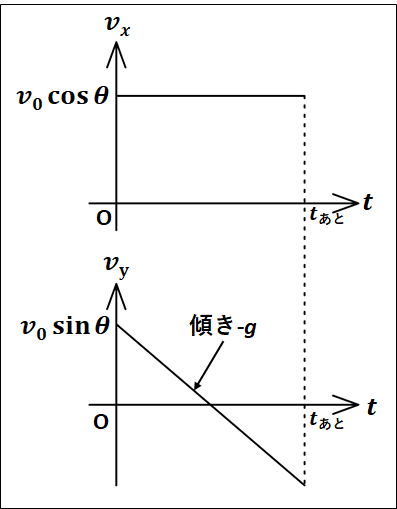
実際に問題を解く際には、この\(v-t\)グラフを用いて面積を求めたり、加速度の定義式を用いていくことになります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


