投稿日:
【高校物理】落下運動①【落下運動】
\(\require{color}\)
\(\require{cancel}\)
落下運動とは、落ちる物体の運動のことです。
これらの問題は、\(v-t\)グラフを描けば解けるのですが、そのために知っておかなけらばならないことがあります。
この記事では、\(v-t\)グラフを描く際の注意点と、落下運動の種類について解説していきます。
落下運動の具体的な問題の解き方については、別記事で練習問題を用意するので、そちらを参考にしてください。
補足解説と練習問題の記事はこちらです
→落下運動①(補足解説と練習問題1)
→落下運動①(補足解説と練習問題2)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.落下運動とは
落下運動とは、その名のとおり落ちる物体の運動のことです。
落下運動の問題を解く上では、\(v-t\)グラフが描ければ、加速度の定義式と\(v-t\)グラフの面積から解くことができますが、\(v-t\)グラフを描くために知っておかなければならないことがあります。
(\(v-t\)グラフについてはこちら→v-tグラフと等加速度直線運動)
下記が、落下運動する物体の\(v-t\)グラフを描く際の注意点になります。
\(\bf{①}\)
原点を決める。
原点は物体が運動をはじめたスタート地点にとる。
\(\bf{②}\)
軸を設定する。
正の方向は、初速度が正となる方向または、物体がこれから進むであろう方向にとる。
\(\bf{③}\)
重力加速度\(g=9.8m/s^2\)は\(v-t\)グラフの傾きを表し、下向きの方向である。
\(v-t\)グラフにおける重力加速度の正負は、設定した軸の正の方向と同じなら正、逆なら負とする。
軸の設定はどの向きを正にとっても良いのですが(問題によっては指定されている)、はじめは\(②\)のような向きにとると分かりやすいと思います。
これから、いくつかの落下運動をみていきますが、特に覚える必要はありません。(\(v-t\)グラフが描ければ解けるから)
ただし、運動の内容と\(v-t\)グラフが、どのように対応しているかは理解するようにしましょう。
また、図の中に静止している人を描いていますが、今後のために”物体の運動は静止している人からみたもの”であることを意識しておきましょう。
2.自由落下
自由落下とは、物体を静かに放した際の運動になります。
(“静かに放す\(\Leftrightarrow\)初速度0m/s” のこと)
ビルの上で物体を静かに放す例を考えてみます。
(重力加速度の大きさは\(9.8m/s^2\))
状況を図示すると、下図のようになります。
先に述べた\(v-t\)グラフを描く際の注意点、\(①~③\)に注目してください。
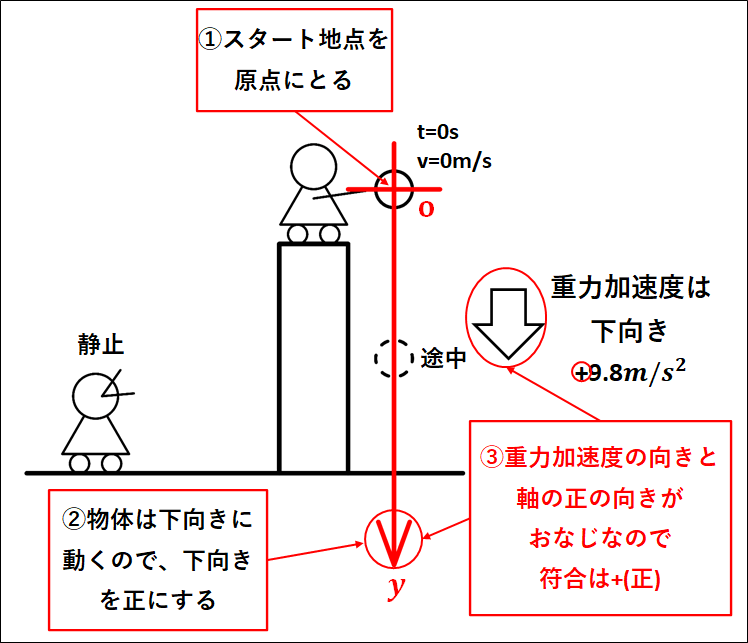
①物体はビルの上から落とされるので、ビルの上の落とされる位置が物体の原点となります。
②物体は落ちて下向きに運動するので、下向きを正にします。
③重力加速度は常に下向きで、今、軸の正の向きも下向きとしています。
重力加速度の向きと、軸の正の向きが同じなので、重力加速度の符合は正(+)になります。
次に、\(v-t\)グラフを描いていきます。
条件としては、\(t=0s\)のとき\(v=0m/s\)(静かに放すので初速度は\(0m/s\))。
重力加速度は、\(v-t\)グラフで扱った際の加速度と同じように\(v-t\)グラフの傾きを表します。
よって、\(v-t\)グラフは右上がりの直線となります。
(重力加速度は\(+9.8m/s^2\)という一定の値なので、グラフは直線となる(等加速度直線運動))
\(v-t\)グラフを図示すると以下のようになります。
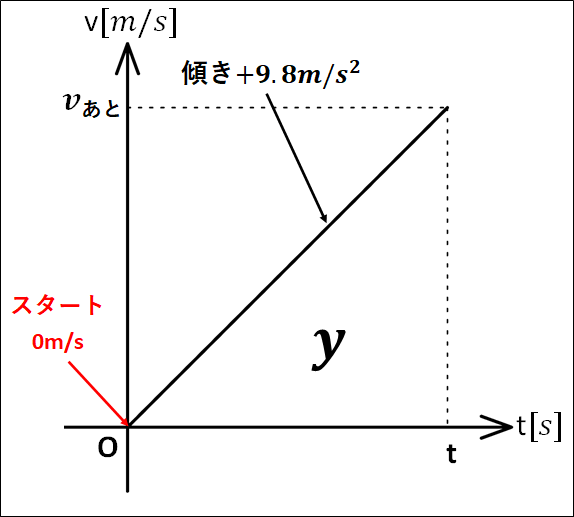
\(v-t\)グラフは手を放してから\(t\)秒後までを描いてあります。
図中の面積\(y\)はグラフが\(t\)軸よりも上にあるので正の面積であり、今、下向きを正にとっているので、物体が下向きに進んだ距離を表します。
(今までは\(x\)と表記していたが、縦方向(鉛直方向)の運動のため\(y\)と表示)
実際に問題を解く際には、与えられた情報と、この\(v-t\)グラフから面積や\(v_{\bf{あと}}\)などを求めていくことになります。
3.鉛直投げ下ろし
自由落下では物体を静かに放しましたが、鉛直投げ下ろしは、真下に向かって物体を投げたときの運動となります。
なので、自由落下との違いは初速度が\(0m/s\)ではないこととなります。
例として、ビルの上から物体を初速度\(v_{0}m/s\)で真下に投げ下ろすことを考えます。
(重力加速度の大きさは\(9.8m/s^2\))
状況を図示すると、下図のようになります。
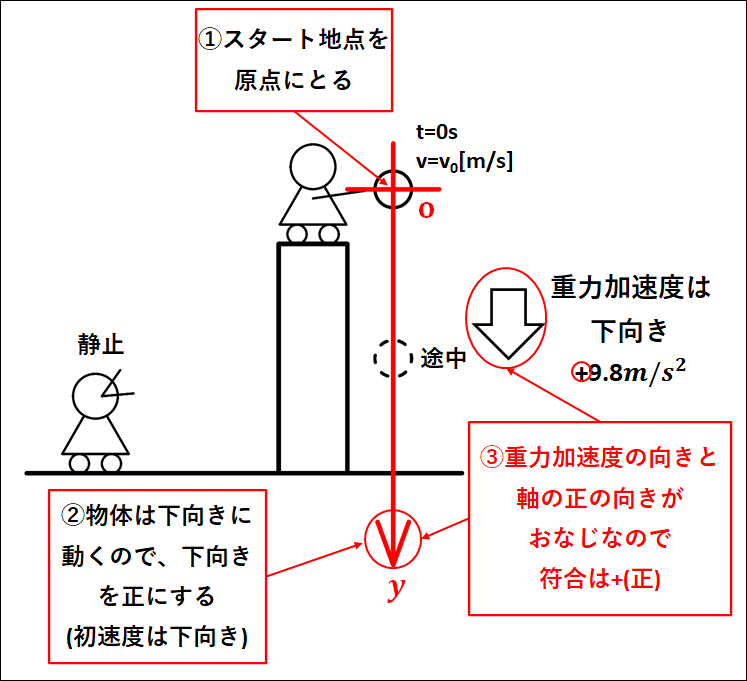
自由落下との図の違いは、\(t=0s\)での初速度が\(0m/s\)ではなく\(v_{0}[m/s]\)となっていることだけです。
次に、\(v-t\)グラフを描いていきます。
条件としては、\(t=0s\)のとき\(v=v_0[m/s]\)。
重力加速度は\(+9.8m/s^2\)と正の値なので、グラフの傾きは右上がりとなります。
\(v-t\)グラフを図示すると以下のようになります。
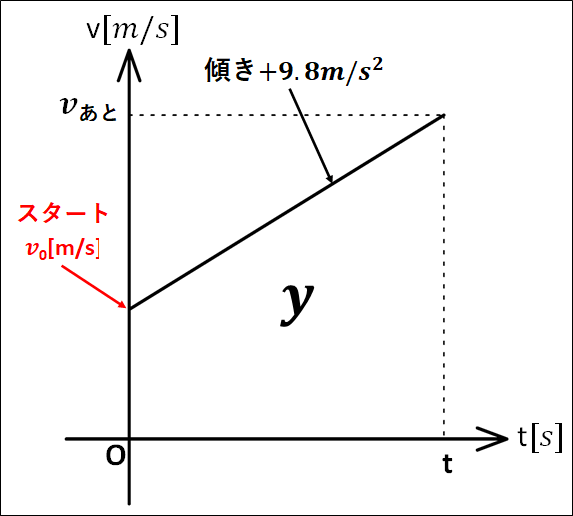
\(v-t\)グラフは物体を投げ下ろしてから\(t\)秒後までを描いてあります。
図中の面積\(y\)はグラフが\(t\)軸よりも上にあるので正の面積であり、今、下向きを正にとっているので、 物体が下向きに進んだ距離を表します。
4.鉛直投げ上げ
鉛直投げ上げは、物体を真上に投げたときの運動になります。
\(\textcolor{red}{\bf{○ポイント}}\)
→上に投げた物体は、最高点で一瞬止まり、その後落ちてくる!!
イメージ図を載せておきます。
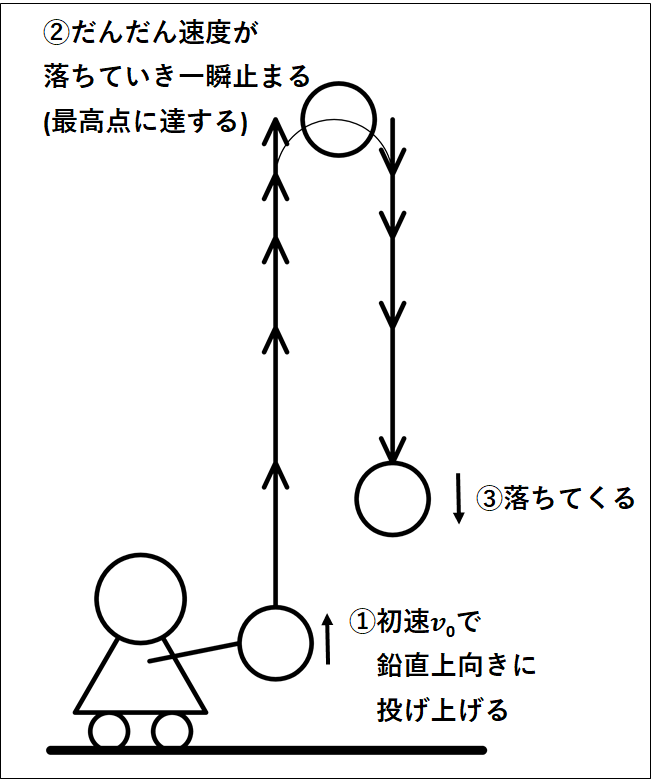
図では見やすくするために、物体が上がっているときと下がっているときをずらして描いていますが、実際には同一直線上を上がってから下がってくると考えてください。
投げ上げた直後は物体は速いですが、重力にひかれてだんだん遅くなっていきます。
その後、最高点で一瞬止まり(速度が\(0m/s\)になり)、その後落ちてきます。
落ちてくるときは、はじめは物体は遅いですが、だんだん速くなっていきます。
例として、物体を初速度\(v_0\)で投げ上げる場合を考えていきます。
(重力加速度の大きさは\(9.8m/s^2\))
状況を図示すると、下図のようになります。
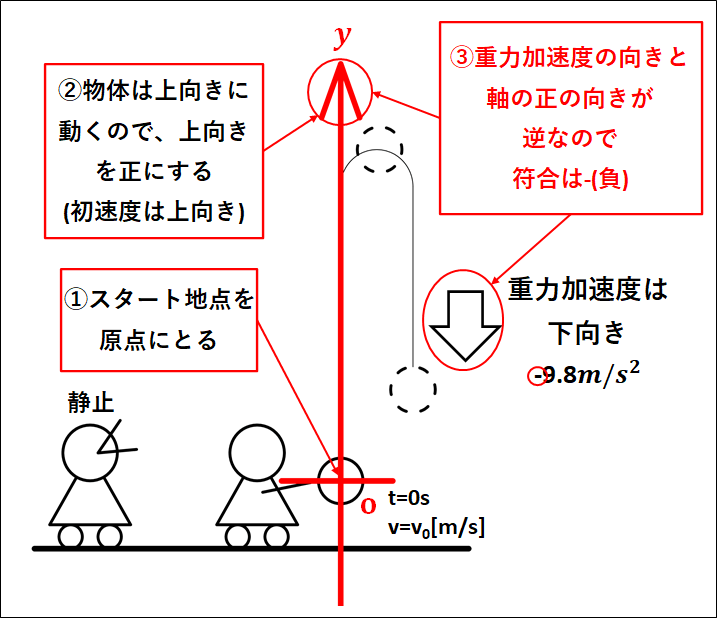
こちらも、物体は同一直線上を上がってから下がってくると考えてください。
①物体は投げ上げられて鉛直上向きに運動をはじめるので、投げ上げられる直前が原点となります。
②物体は投げ上げられて、鉛直上向きに運動するので上向きを正とします。
③重力加速度は常に下向きで、今、軸の正の向きは上向きとしています。
重力加速度の向きと、軸の正の向きが逆なので、重力加速度の符合は負(-)になります。
次に、\(v-t\)グラフを描いていきます。
条件としては、\(t=0s\)のとき\(v=v_0[m/s]\)
重力加速度は、\(v-t\)グラフの傾きを表しますが、今回は値が負なのでグラフは右下がりの直線になります。
\(v-t\)グラフを図示すると以下のようになります。
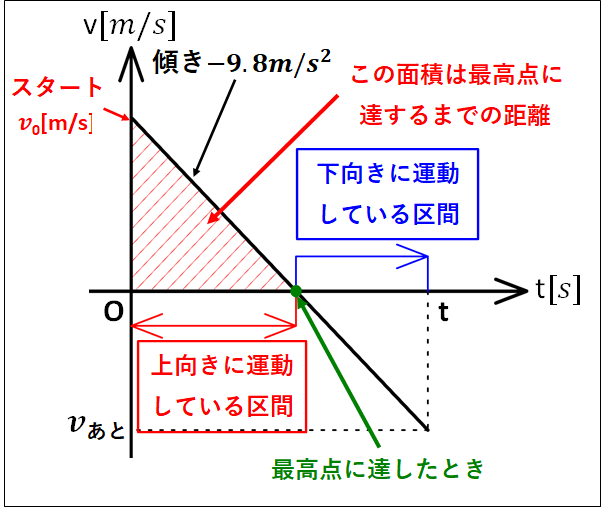
\(v-t\)グラフは物体を投げ下ろしてから\(t\)秒後までを描いてあります。
\(v-t\)グラフから、グラフの傾きが右下がりなので時間の経過とともに速度が初速度\(v_0\)からだんだん遅くなっていることが分かると思います。
そして、\(t\)軸とグラフが交わる点では速度\(0m/s\)となるので、ここが最高点に達する点となります。
グラフが\(t\)軸よりも上の部分は正の面積となります。
今、上向きを正としているので、正の面積は上向きに進んだ距離を表しています。
また、グラフが\(t\)軸よりも下側の部分は速度が負となっており、上向きを正としているので速度は下向きであることを表しています。
この部分の面積に関しては、負の面積となり、現在上向きを正としているので下向きに進んだ距離を表しています。
落下運動には他にも水平投射や斜方投射などがありますが、今後解説する運動方程式を学んでからの方が理解しやすいと思うので、運動方程式を学んだあとに解説します。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


