投稿日:
【高校物理】力のはたらきとつりあい【力】【つりあい】【作用・反作用】
\(\require{color}\)
\(\require{cancel}\)
この記事は力のつりあいの条件や、各種力についての解説記事になります。
力については、非接触力や接触力、物体にかかっている力の見つけ方についても述べていきます。
また、水圧ρdgや浮力ρVgの導き方についても解説しています。
作用反作用については、「つりあいの力」と「作用・反作用の力」の違いについても解説しています。
補足解説と練習問題の記事はこちらです
→力の見つけ方
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.力のつりあい
物体が静止しているとき、物体にかかっている力は\(\textcolor{red}{\bf{つりあっています}}\)。
力が左右方向と上下方向にかかっている場合の、つりあいの条件は
①
物体にかかっている上向きの力の合力と下向きの力の合力の大きさが同じで、同一直線上にある。
②
物体にかかっている右向きの力の合力と左向きの力の合力の大きさが同じで、同一直線上にある。
となります。
(力の向きが逆で、大きさが同じ)
上記では、上下左右方向での条件でしたが、自分で\(x-y\)座標を定めた場合には、\(x\)軸方向と\(-x\)軸方向、\(y\)軸方向と\(-y\)軸方向の力の合力の大きさが同じという条件になります。
また、上記のことは物体にかかっている力のベクトルの合力が\(0\)であることを意味しています。
すなわち、物体にかかっている力が、\(F_1,F_2,F_3\cdots\)のとき、物体が静止している(つりあっている)なら
\(\displaystyle{\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots=\vec{0}}\)
となります。
\(F_1,F_2,F_3\cdots\)をそれぞれ\(x\)軸方向と\(y\)軸方向に分解して、成分で考えてみます。
(力の分解についてはこちら→力とベクトル)
それぞれの力の成分表示が
\(\displaystyle{\vec{F_1}=\left(\begin{eqnarray}&&F_{1x}\\&&F_{1y}\end{eqnarray}\right)}\)
\(\displaystyle{\vec{F_2}=\left(\begin{eqnarray}&&F_{2x}\\&&F_{2y}\end{eqnarray}\right)}\)
\(\displaystyle{\vec{F_3}=\left(\begin{eqnarray}&&F_{3x}\\&&F_{3y}\end{eqnarray}\right)}\)
\(\displaystyle{\vdots}\)
とすると、
\(\displaystyle{\begin{eqnarray}&&\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots=\vec{0}\\\\\Leftrightarrow&&{\left(\begin{array}{c}F_{1x}\\F_{1y}\end{array}\right)}+{\left(\begin{array}{c}F_{2x}\\F_{2y}\end{array}\right)}+{\left(\begin{array}{c}F_{3x}\\F_{3y}\end{array}\right)}+\cdots={\left(\begin{array}{c}0\\0\end{array}\right)}\end{eqnarray}}\)
となり、成分のみで考えると物体がつりあう際には
\(\displaystyle{F_{1x}+F_{2x}+F_{3x}+\cdots=0}\)
↑
\(x\)軸方向の合力が\(0\)(\(x\)軸方向のつりあい)
\(\displaystyle{F_{1y}+F_{2y}+F_{3y}+\cdots=0}\)
↑
\(y\)軸方向の合力が\(0\)(\(y\)軸方向のつりあい)
となります。
2.非接触力と接触力
力には\(\textcolor{green}{\bf{非接触力}}\)と\(\textcolor{red}{\bf{接触力}}\)があります。
\(\textcolor{green}{\bf{○非接触力}}\)
物体同士が触れ合っていなくてもはたらく力。
\(\textcolor{red}{\bf{○接触力}}\)
物体同士が触れ合ってはたらく力。
例として、代表的な力の種類と力の向きを載せておきます。
○重力(\(\textcolor{green}{\bf{非接触力}}\))
向き:鉛直下向き
○張力(\(\textcolor{red}{\bf{接触力}}\))
向き:糸が抜ける向き
○弾性力(\(\textcolor{red}{\bf{接触力}}\))
向き:伸び、縮みと逆の方向(ばねが自然長に戻ろうとする方向)
○垂直抗力(\(\textcolor{red}{\bf{接触力}}\))
向き:接触面、接触点と直角で、自分を貫く方向。
次から、上記に載せた代表的な力に加えて、様々な力について解説していきます。
3.重さと質量
物体にはたらく重力の大きさを”物体の重さ”といいます。
重力の大きさは、
質量:\(m[kg]\)
重力加速度:\(g[m/s^2]\)
を用いて、
\(\textcolor{red}{\bf{mg[N]}}\)
と表されます。
(質量×重力加速度)
質量の\(m\)は\(mass\)(質量)の頭文字、重力加速度の\(g\)は\(gravitational acceleration\)(重力加速度)の頭文字となります。
重力の単位に用いられている”\(N\)”(ニュートン)は力の単位であり、質量と重力加速度を掛けると単位は
\(kg・m/s^2\)
となるので、\(kg・m/s^2\)の別の表し方となります。
(\(N=kg・m/s^2\))
この\(N\)は、\(kg・m/s^2\)からも分かる通り、\(1kg\)の物体に\(1m/s^2\)の加速度を生じさせる力の単位となります。
体重計などで表示される数値は、質量ではなく重さ(重力の大きさ)となります。
重力の向きは物体の中心から鉛直下向き(地球の中心方向)となり、\(\textcolor{green}{\bf{非接触力}}\)で\(\textcolor{red}{\bf{物体に常にはたらきます}}\)。
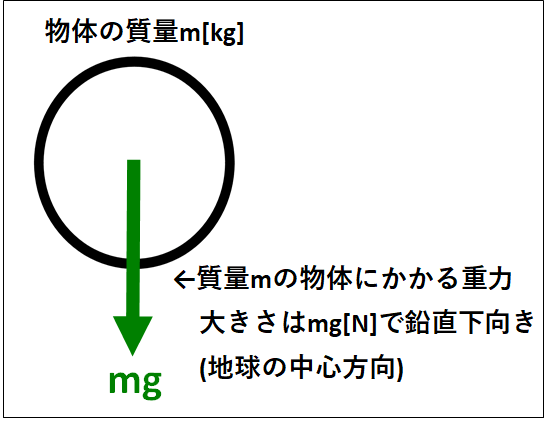
※
質量とは、物体の状態の変わりにくさを表す量です。
↓
・静止している物体は、質量が大きいほど動かしにくい。
・運動している物体は、質量が大きいほど止めにくく、運動の方向も変えにくい。
4.張力
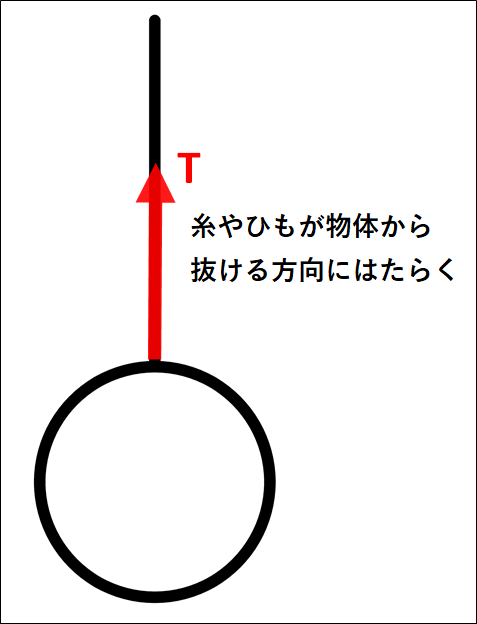
張力はたいてい文字”\(T\)”(\(tention\):張力 の頭文字)で表され、物体から糸やひもが抜ける方向にはたらきます。
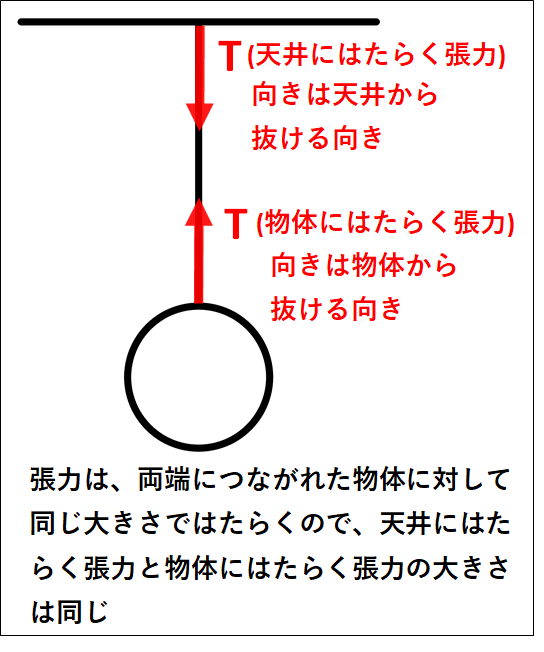
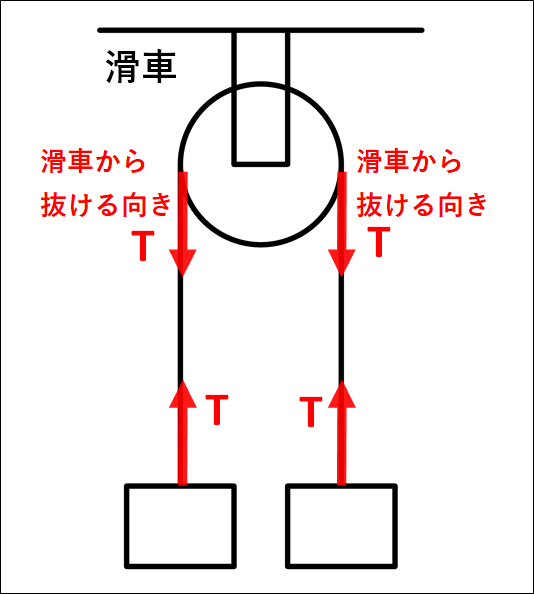
また、張力は”糸やひもの両端につながれた物体に対して、同じ大きさ”ではたらきます。
張力も力なので、単位は\(N\)(ニュートン)で、\(\textcolor{red}{\bf{接触力}}\)となります。
たいていの場合は問題文中に、”軽い糸”や”軽いひも”と記述されており、軽いというのは”質量を無視できる”ということです。
なので上記の記述があった際には、普通重力は常にはたらきますが、糸やひも自体の重力は考えなくてもよいです。
5.ばねの弾性力
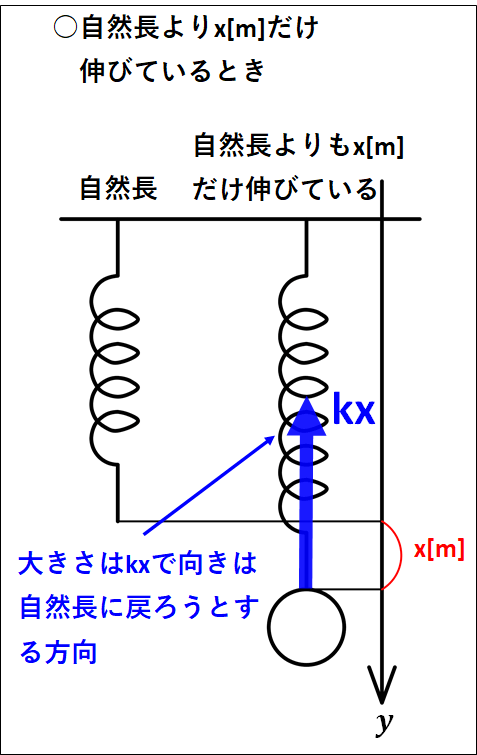
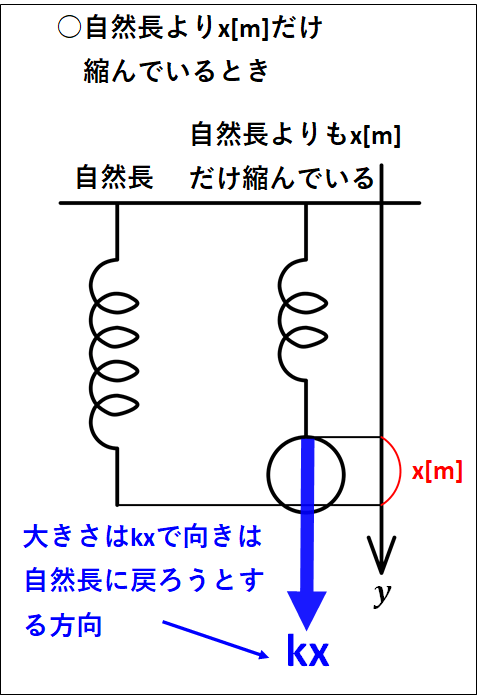
ばねに力が加わっていないときのばねの長さを”自然長”といい、ばねを自然長よりも伸ばしたり縮めたりしたときにばねは自然長に戻ろうとします。
このばねが自然長に戻ろうとする力をばねの”弾性力”といいます。
ばねの弾性力の向きは、自然長に戻ろうとする方向となります。
すなわち、ばねが伸びていれば縮む方向に、ばねが縮んでいれば伸びる方向が弾性力の向きとなります。
また、ばねの弾性力の大きさは、ばねの自然長からの伸びや縮みに比例します。
ばねの伸びまたは縮みを\(x[m]\)、比例定数を\(k[N/m]\)とするとばねの弾性力の大きさは
\(\displaystyle{kx[N]}\)
と表せます。
(比例定数×伸びor縮み)
単位は、比例定数と伸びまたは縮みを掛けているので\(N/m×m=N\)となります。
上記比例定数\(k\)を”ばね定数”といいます。
ばねの弾性力は\(\textcolor{red}{\bf{接触力}}\)です。
6.水圧
\(\bf{\underline{○圧力について}}\)
圧力とは、流体中(気体や液体)の物体が、流体から面に対して垂直に受ける力のことです。
単位面積(\(1m^2\))あたりに受ける力(\(N\))であり、単位は\(N/m^2\)(ニュートン毎平方メートル)となります。
また、\(N/m^2\)を別の単位\(Pa\)(パスカル)で表すことが多いです。(\(Pa=N/m^2\))
圧力を\(P\)(\(pressure\):圧力 の頭文字)とすると、この圧力\(P\)は次式で表されます。
\(\displaystyle{P[Pa]=\frac{F[N]}{S[m^2]}}\)
\(F[N]\)は面にかかっている力、\(S[m^2]\)は力がかかっている面積です。
上式は、圧力は力を面積で割ったものであることを表しています。
また、この式から力\(F[N]\)は圧力\(P\)と面積\(S\)で表すと
\(\displaystyle{F[N]=P[N/m^2]×S[m^2]}\)
であることが分かります。
(圧力の式の両辺に\(S[m^2]\)を掛けた。力=圧力×面積)
特に、地上における大気の圧力を大気圧といい、その大きさ\(P_0\)は約\(1.0×10^5Pa\)です。
この大気圧は、”大気の重さ”によって発生します。
\(\bf{\underline{○水圧}}\)
水圧とは、水中の物体が水から受ける圧力のことです。
水圧も、大気圧が大気の重さが原因で発生するのと同様に、”水の重さ”が原因で発生します。
ここから、水中の物体にはたらく圧力を考えていきます。
水の密度(単位体積(\(1m^3\))あたりの質量(\(kg\)))を\(ρ[kg/m^3]\)(\(ρ\)はローと読む)とし、水面から深さ\(d[m]\)の物体にはたらく圧力を考えます。
水中の物体の圧力を考えるにあたって、大気と水の角柱を考えて、この角柱の断面積を\(S[m^2]\)とします。
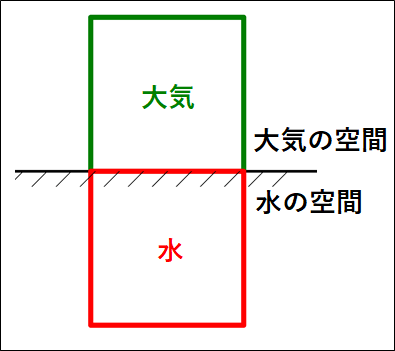
↓
大気と水を一体として考えます。
\(\textcolor{green}{m_{\bf{大}}}\)を大気の質量、\(\textcolor{red}{m_{\bf{水}}}\)を水の質量とします。
↓
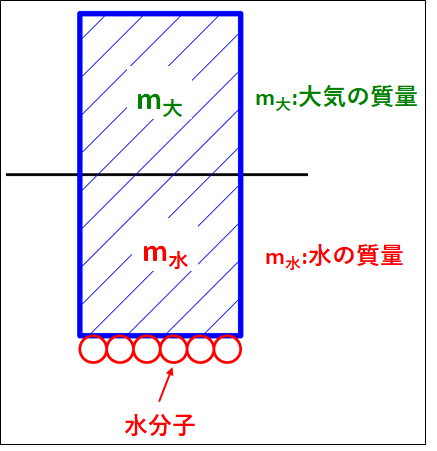
ここで、角柱の底面の水分子のつりあいについて考えます。
水分子の上には大気と水の重さ(重力)が下向きにかかっています。
水分子がつりあうためには、逆向きの力が加わっている必要があるので、これを上向きの力\(F\)(圧力による力)とします。
図示すると下図のようになります。
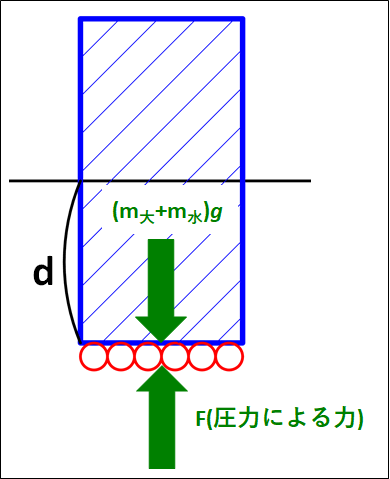
つりあうためには、上向きと力と下向きの力の大きさが等しければいいので、

上式において、力\(F\)は先ほど説明したように下から水分子にはたらく圧力を\(P\)とすると
\(\displaystyle{P=\frac{F}{S}}\)から\(F=P・S\)
大気圧は、大気の重さによって発生するので大気による重力は
\(m_{\bf{大}}g=P_0S\)
と、大気圧による力と同じものです。
また今、水の密度を\(ρ\)としているので、水の質量\(m_{\bf{水}}\)は\(Sdρ\)となります。
※
\(S[m^2]×d[m]\)で水部分の角柱の体積。
水の密度は\(ρ[kg/m^3]\)(単位体積あたりの質量)なので、これに体積を掛けると水の質量となる。
\(\displaystyle{\begin{eqnarray}&&S[m^2]×d[m]×ρ[kg/m^3]\\&=&Sd[m^3]×ρ[kg/m^3]\\\\&=&Sdρ[kg]\end{eqnarray}}\)

以上のことから、つりあいの式を変形していって

式の結果から、水圧は
\(\displaystyle{\textcolor{red}{ρdg}[N/m^2]}\)
で表され、水深(\(d[m]\))が深いほど大きくなることが分かります。
また、水面から深さ\(d[m]\)の物体にはたらく圧力\(P\)は
\(P=P_0+ρdg\)
で表されることが分かります。
7.浮力
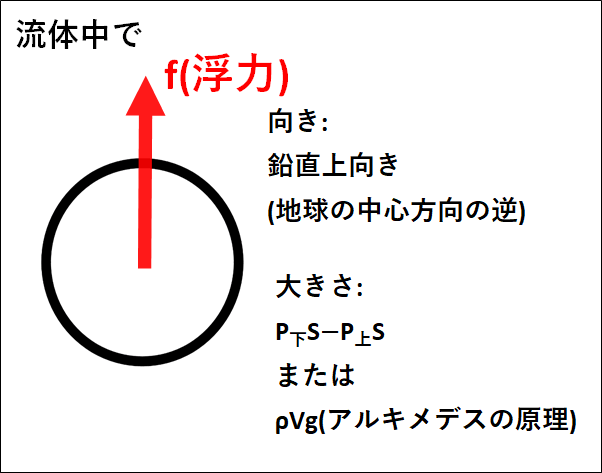
浮力とは、流体中の物体が流体から受ける力で、向きは”鉛直上向き”となります。
流体中の物体の、上面にかかる圧力と下面にかかる圧力の差によって発生します。
浮力がどのように表されるかについて考えていきます。
水の密度を\(ρ[kg/m^3]\)、物体を各面\(S[m^2]\)の立方体とし、下図のような状態を考えます。
(水圧は面に対して垂直にかかる)
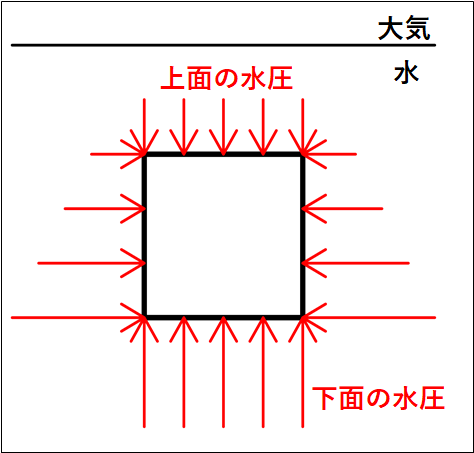
水圧は\(ρdg\)から深さが同じところでは同じ大きさとなります。
よって、左右方向の力はつりあうので、上下方向のみを考えます。
物体の上面にかかる水圧を\(P_{\bf{上}}\)、下面にかかる水圧を\(P_{\bf{下}}\)とすると、水圧による力はそれぞれ\(P_{\bf{上}}S\)、\(P_{\bf{下}}S\)となります。
水面から物体の上面までの距離を\(h[m]\)、物体の高さを\(d[m]\)とすると、下図のようになります。
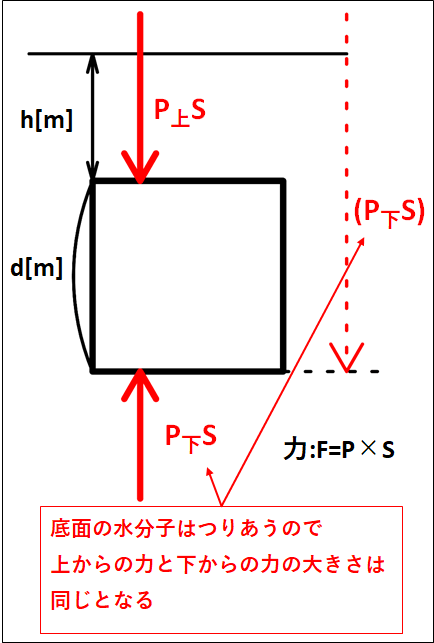
図から水圧は深い方が大きくなるので\(P_{\bf{上}}S{\lt}P_{\bf{下}}S\)。
よって、浮力の大きさを\(f\)とすると\(f=P_{\bf{下}}S-P_{\bf{上}}S\)となります。
(浮力は、上面と下面の水圧による力の差。上面にかかる力より下面にかかる力の方が大きいので、浮力は鉛直上向き)
また、水圧の部分で述べたように、水圧は\(\displaystyle{\textcolor{red}{ρdg}[N/m^2]}\)で表されます。
\(d\)は深さを表しますが、物体の上面までの深さは\(h[m]\)、下面までの深さは\((h+d)[m]\)です。
実際に浮力\(f\)を計算してみると
\(\displaystyle{\begin{eqnarray}f&=&P_{\bf{下}}S-P_{\bf{上}}S\\\\&=&{P_0+ρ(h+d)g}S-{P_0+ρhg}S\\\\&=&P_0S+ρ(h+d)Sg-(P_0S+ρhSg)\\\\&=&P_0S+ρhSg+ρdSg-(P_0S+ρhSg)\\\\&=&ρdSg\end{eqnarray}}\)
よって、浮力\(f\)は
\(f=ρdSg[N]\)
で表されます。
この\(ρdSg\)の意味は以下のようなものになります。
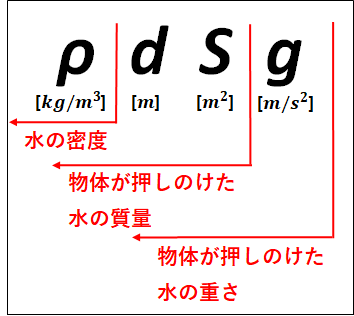
また、上式の\(dS\)は物体の体積を表しているので、これを体積\(V\)で書きなおすと、
\(ρdSg=ρVg\)
となります。
単位をみてみると、
\(kg/m^3×m^3×m/s^2=kg・m/s^2=N\)
と、力の単位となっています。

上記の式を”アルキメデスの原理”といい、流体中の物体にはたらく浮力は、その物体が押しの出た流体の重さに等しいことを表しています。
問題を解く上で、
浮力:\(P_{\bf{下}}S-P_{\bf{上}}S\)
アルキメデスの原理:\(ρVg\)
のどちらの式を使うのかについてですが、問題文中に大気圧\(P_0\)があらわれたのなら、\(P_{\bf{下}}S-P_{\bf{上}}S\)を用います。
(アルキメデスの原理に\(P_0\)は現れないから)
下記に、浮力の向きと大きさを図示しておきます。
8.抗力
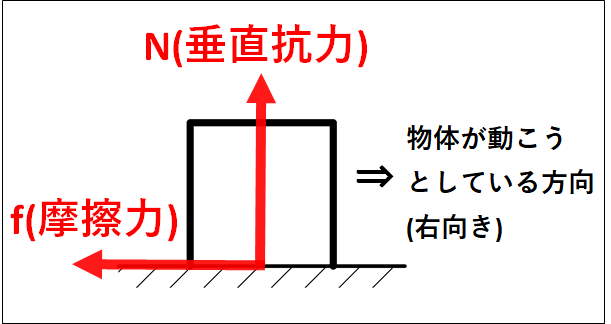
抗力とは、物体が接触面や接触点から受ける力のことです。
特に、面に垂直な成分を\(\textcolor{red}{\bf{垂直抗力}}\)、面に平行な成分を\(\textcolor{red}{\bf{摩擦力}}\)といいます。
抗力は、\(\textcolor{red}{\bf{接触力}}\)です。
垂直抗力\(N\):
接触面や接触点に垂直で、自分を貫く方向にはたらく。
摩擦力\(f\):
接触面や接触点に平行で、物体が動こうとする向きと逆向きにはたらく。
摩擦力については、次で詳しく解説します。
9.摩擦力
摩擦力には、\(\textcolor{red}{\bf{静止摩擦力}}\)と\(\textcolor{red}{\bf{動摩擦力}}\)があります。
摩擦力がはたらいていても、物体が静止しているときには静止摩擦力が、物体が動いているときには動摩擦力がはたらきます。
この2つの摩擦力について説明していきます。
\(\bf{\underline{○静止摩擦力}}\)
“粗い面上”の物体にかかり、物体が動こうとする向きと逆向きにかかります。
粗い面上の物体に力を加えても、小さい力では物体は動きません。
これは、物体が動こうとする向きと逆向きに静止摩擦力がかかるからです。
物体に加える力を大きくしていくと、静止摩擦力も大きくなっていき、物体が動き出す直前で最大となります。
物体が”静止”しているときの摩擦力を”\(\textcolor{red}{\bf{静止摩擦力}}\)”といい、動き出す直前の摩擦力を”\(\textcolor{red}{\bf{最大静止摩擦力(最大摩擦力)}}\)”といいます。
実験から、最大静止摩擦力\(f_0[N]\)は、物体にはたらく垂直抗力の大きさ\(N[N]\)に比例し、
\(f_0=μN\)
と表されることがわかっています。
\(μ\)はミューと読み、この比例定数を”\(\textcolor{red}{\bf{静止摩擦係数}}\)”といいます。
\(\bf{\underline{○動摩擦力}}\)
“\(\textcolor{red}{\bf{動摩擦力}}\)”は粗い面上で、物体が”動いているとき”にはたらく摩擦力になります。
実験から、動摩擦力\(f^{\prime}[N]\)は垂直抗力の大きさ\(N[N]\)に比例し、
\(f^{\prime}=μ^{\prime}N\)
と表されることがわかっています。
上記の比例定数\(μ^{\prime}\)を”\(\textcolor{red}{\bf{動摩擦係数}}\)”といいます。
静止摩擦力は、力を加えていくと大きくなっていきますが、最大静止摩擦力を越えて物体が動き出すと、このときの動摩擦力は”一定の値”となります。
\(\bf{\underline{○摩擦力と力のグラフ}}\)
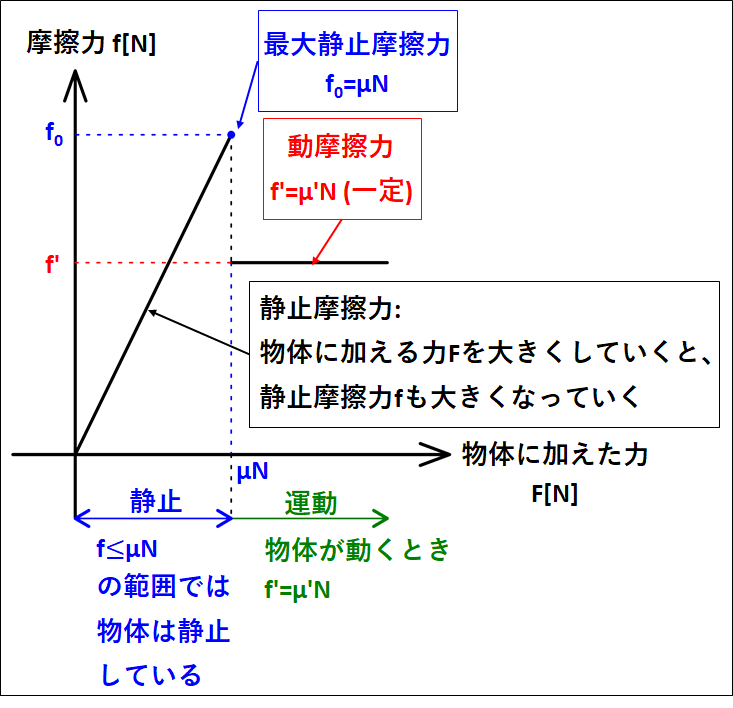
摩擦力(静止摩擦力と動摩擦力)と物体に加えた力\(F\)の関係を表したグラフを載せておきます。
物体に加えた力が大きくなっていくと、静止摩擦力も大きくなってく様子や、最大静止摩擦力を超えると物体が動き出し、動摩擦力がはたらく様子を観察してください。
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{\begin{eqnarray}&&{\bf{物体は静止する}}\\\Leftrightarrow&&f{\le}μN (静止摩擦力)\\\\&&μ:{\bf{静止摩擦係数}}\end{eqnarray}}\)
\(\textcolor{red}{\begin{eqnarray}&&{\bf{物体は動いている}}\\\Leftrightarrow&&f^{\prime}=μ^{\prime}N (動摩擦力)\\\\&&μ^{\prime}:{\bf{動摩擦係数}}\end{eqnarray}}\)
また、一般に
\(μ^{\prime}{\lt}μ\)
(動摩擦係数<静止摩擦係数)
10.物体にかかっている力の見つけ方
物体にかかっている\(\textcolor{red}{\bf{接触力}}\)をみつけるには、注目している物体の表面をなでまわすと良いです。
なでまわしたときに、当たる部分があるのでそこに何らかの力がかかっています。
(あたる部分がなければ、接触力ははたらいていない)
\(\textcolor{green}{\bf{非接触力}}\)
→重力は、必ず物体にはたらく
\(\textcolor{red}{\bf{接触力}}\)
→物体の表面をなでまわしたときに当たる、面や点にはたらく
例として、次のような状況について考えていきます。
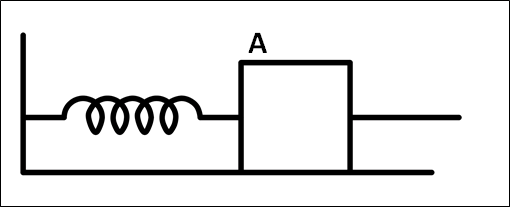
例)
質量\(m\)の物体\(A\)の左側にばねが取り付けられ、右側に軽いひもがつけられている。
この物体\(A\)が右向きに引っ張られて、ばねが自然長から\(x\)だけ伸びており、この状態で静止している。
床はなめらかで、ばね定数を\(k\)、重力加速度を\(g\)とする。
まず、非接触力について考えます。
物体\(A\)には非接触力である重力がはたらいています。
物体\(A\)の質量は\(m\)なので、重力の大きさは\(mg\)(質量×重力加速度)で、鉛直下向きにはたらきます。
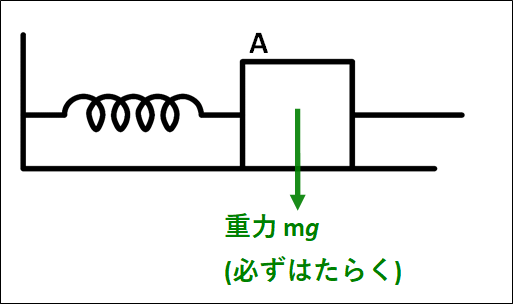
次に、接触力について考えていきます。
先ほど述べたように、物体の表面をなでまわしてみます。
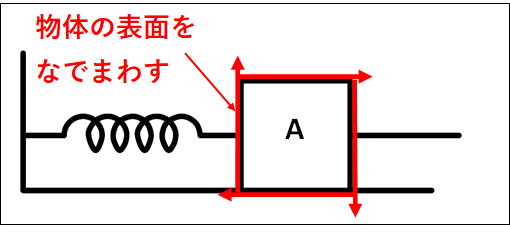
そうすると、なでまわしている最中にあたる部分があることがわかると思います。
この部分に接触力がはたらいています。
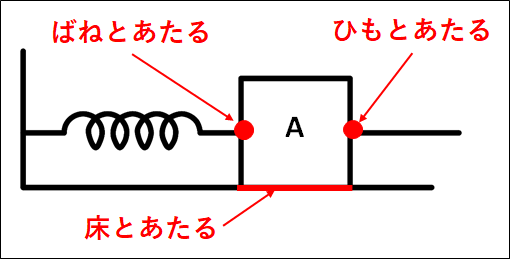
これで、接触力がはたらいている部分はわかりました。
次に、接触力の種類について考えていきます。
\(\bf{\underline{○ばねとあたっている部分}}\)
この部分は、ばねとあたっているので”ばねの弾性力”がはたらいています。
いま、物体は右向きに引っ張られており、ばねは\(x\)だけ伸びているので、この弾性力の大きさは\(kx\)となります。
向きは、ばねが右向きに伸びているので、自然長に戻ろうとする左向きとなります。
\(\bf{\underline{○ひもとあたっている部分}}\)
この部分はひもとあたっているので張力となります。
この張力を\(T\)としておきます。
向きは、ひもが抜ける方向なので、右向きとなります。
\(\bf{\underline{○床とあたっている部分}}\)
この部分には抗力がはたらいていますが、床はなめらかなので摩擦力ははたらいておらず、垂直抗力のみがはたらいています。
(摩擦力は粗い面ではたらく。なめらかな面でははたらかない)
この垂直抗力を\(N\)としておきます。
向きは、面と垂直で自分(物体\(A\))を貫く方向になるので、鉛直上向きとなります。
以上を図示すると、下図のようになります。
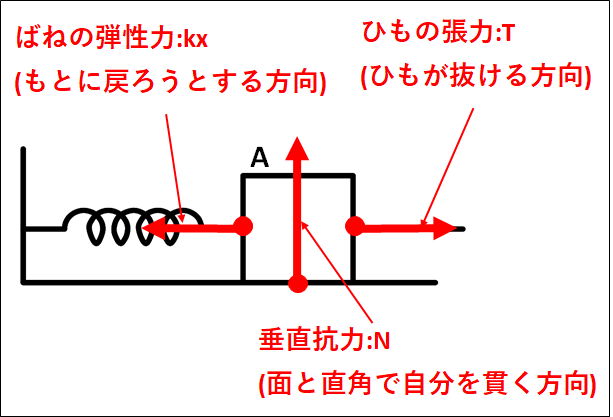
物体\(A\)にかかっているすべての力を図示すると、以下のようになります。
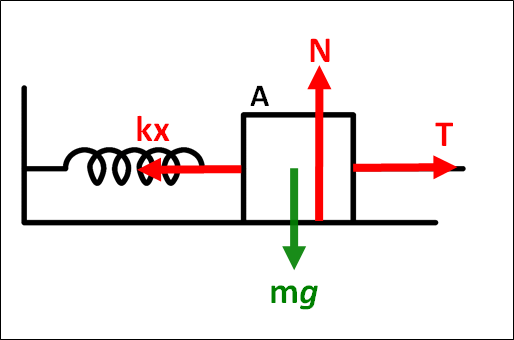
ついでに、物体は静止しているのでつりあいの条件も確認しておきます。
物体が静止する(つりあう)条件は、上向きの力と下向きの力の大きさが等しい、右向きの力と左向きの力の大きさが等しい、なので
\(\displaystyle{\left\{\begin{eqnarray}&&{\bf{(上向きの力)}}={\bf{(下向きの力)}}\\&&{\bf{(右向きの力)}}={\bf{(左向きの力)}}\end{eqnarray}\right.}\)
となります。
今、図示した力から
上向きの力→垂直抗力:\(N\)
下向きの力→重力:\(mg\)
右向きの力→張力:\(T\)
左向きの力→弾性力:\(kx\)
なので、物体が静止する条件(つりあいの条件)は以下のようになります。

また、つりあいの条件を立てることで、静止しているときの物体にはたらく未知の力の大きさがわかります。
上記の例でいうと、ひもの張力\(T\)と垂直抗力\(N\)の力の大きさは分かりませんでしたが、つりあいの条件を立式したことでそれぞれ\(mg\)と\(kx\)であることがわかりました。
11.作用・反作用の法則
\(A\)さんが\(B\)さんを手で押すときを考えてみます。
\(A\)さんに注目すると、\(A\)さんの手は\(B\)さんにあたっているので\(A\)さんは\(B\)さんから垂直抗力を受けます。
逆に\(B\)さんに注目すると、\(B\)さんは\(A\)さんに手をあてられているので、\(B\)さんは\(A\)さんから垂直抗力を受けます。
それぞれの垂直抗力は、自分を貫く方向となるので、\(A\)さんにはたらいている垂直抗力と\(B\)さんにはたらいている垂直抗力の向きは逆向きとなります。
しかし、与えているまたは、与えられている力の大きさは同じなので、この2つの垂直抗力の大きさは同じになります。
このような同じ大きさで逆向き、また同一直線上にある、お互いに及ぼしあっている力の一方を作用、もう一方を反作用といいます。
一般的に、2つの物体が互いに力を及ぼし合うとき、作用と反作用は同一直線上にあり、逆向きで大きさが等しくなります。
これを、”\(\textcolor{red}{\bf{作用・反作用の法則}}\)”といいます。
(逆向き、同じ大きさ、同一直線上の力のペア)
また、”作用・反作用の法則”を”運動の第三法則”ともいいます。
上記に関して、実際に力を図示してみます。
例として、なめらかな床の上(氷など)で、静止している\(A\)が静止している\(B\)を押すことを考えます。
状況を図示すると以下のようになります。
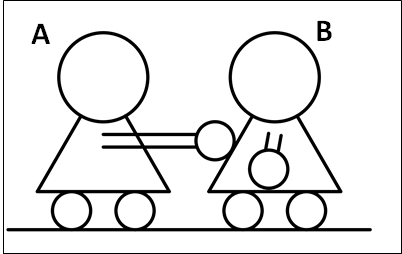
次に、\(A\)、\(B\)それぞれについて注目して、かかっている力を考えていきます。
\(\bf{\underline{○Aについて}}\)
\(A\)に注目します。
まず、非接触力である重力が鉛直下向きにかかっているので、これを\(m_Ag\)とします。
次に、床から垂直抗力を受けます。
向きは、床と垂直で自分を貫く方向なので鉛直上向きにはたらきます。
この垂直抗力を\(N_A\)とします。
最後に、\(A\)は\(B\)を押しているので、この接触点で垂直抗力がはたらいています。
この垂直抗力を\(N\)とすると、\(N\)は自分を貫く方向である左向きにはたらきます。
これらすべての力を図示すると、下図のようになります。
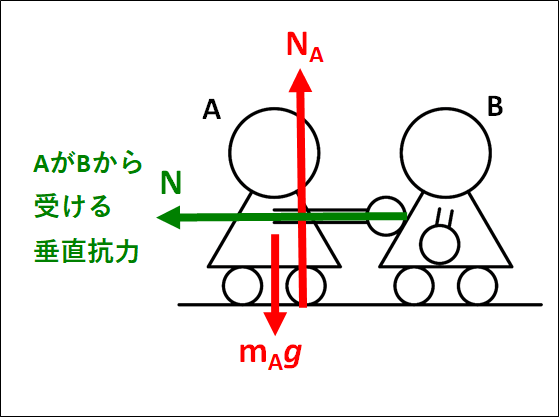
床からの垂直抗力\(N_A\)は、\(A\)をなでまわすと足が2点で接していますが、各足にはたらく垂直抗力の合力を\(N_A\)としています。
\(\bf{\underline{○Bについて}}\)
次に\(B\)に注目します。
まず、非接触力である重力が鉛直下向きにかかっているので、これを\(m_Bg\)とします。
次に、床から垂直抗力を受けます。
向きは、床と垂直で自分を貫く方向なので鉛直上向きにはたらきます。
この垂直抗力を\(N_B\)とします。
最後に、\(B\)は\(A\)に押されているので、この接触点で垂直抗力がはたらいています。
この垂直抗力を\(N\)とすると、\(N\)は自分を貫く方向である右向きにはたらきます。
これらすべての力を図示すると、下図のようになります。
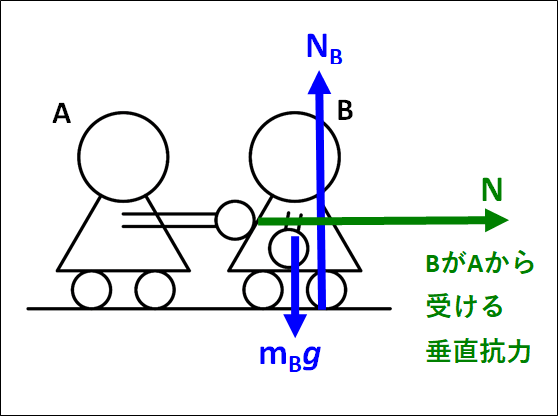
床からの垂直抗力\(N_B\)は、\(B\)をなでまわすと足が2点で接していますが、各足にはたらく垂直抗力の合力を\(N_B\)としています。
上の\(A\)に注目した場合にかかっている力と、\(B\)に注目した場合にかかっている力を見比べてみると、垂直抗力\(N\)は\(B\)が\(A\)から受けている力であると同時に、\(A\)が\(B\)から受けている力でもあります。
なので、この\(A\)が受けている垂直抗力と\(B\)が受けている垂直抗力は”作用・反作用”の関係となっています。
(逆向き、同じ大きさ、同一直線上のペア)
※
\(A\)について、上下方向では垂直抗力\(N_A\)と重力\(m_Ag\)がつりあいますが(上下方向には動かない)、左右方向については、左向きの垂直抗力\(N\)に対して、右向きの力がありません。
また\(B\)について、上下方向では垂直抗力\(N_B\)と重力\(m_Bg\)がつりあいますが(上下方向には動かない)、左右方向については、右向きの垂直抗力\(N\)に対して、左向きの力がありません。
なので、\(A\)と\(B\)は上下方向には動かないですが、左右方向には動きます。
はじめは\(A\)と\(B\)はともに静止しているので、\(A\)が\(B\)を押すと、\(A\)は垂直抗力\(N\)がはたらく左方向へ、\(B\)は垂直抗力\(N\)がはたらく右方向へそれぞれ動きます。
\(A\)が\(B\)を押した場合でも、なめらかな床の上では両者とも逆方向へと動くのは作用・反作用の力がはたらいているからということになります。
また、作用・反作用の法則は”接触力だけでなく、非接触力についても成り立ちます”。
作用・反作用例)
接触力の例:
\(A\)が床から受ける垂直抗力について
\(A\)は床から垂直抗力\(N_A\)を受けているが、床に注目すると、床も\(A\)から垂直抗力\(N_A\)を受けている。
\(A\)が受ける垂直抗力は鉛直上向き
床が受ける垂直抗力は、床を貫く方向である鉛直下向き
この\(A\)が床から受ける垂直抗力と、床が\(A\)から受ける垂直抗力は作用・反作用の関係にあります。
(逆向き、同じ大きさ、同一直線上のペア)
非接触力の例:
\(A\)が受ける重力について
\(A\)は地球の中心方向に引っ張られる重力\(m_Ag\)を受けているが、地球に注目すると、地球も\(A\)に引っ張られる重力\(m_Ag\)を受けている。(2つの物体がお互いに引き付けあう力を万有引力という)
\(A\)が地球から受ける重力は
\(A\)の中心→地球の中心
に向かう向き。
地球が\(A\)から受ける重力は
地球の中心→\(A\)の中心
に向かう向き。
この\(A\)が地球から受ける重力と、地球が\(A\)から受ける重力は作用・反作用の関係にあります。
(逆向き、同じ大きさ、同一直線上のペア)
また、「つりあいの力」と「作用・反作用の力」について、間違うこともあるので、この2つの違いについて述べておきます。
つりあいの力
→同一の物体が受ける力
作用・反作用の力
→”異なる2つの物体”が及ぼしあう力
となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


