投稿日:
【高校物理】運動の3法則と束縛条件【運動方程式】【束縛条件】【空気抵抗】
\(\require{color}\)
\(\require{cancel}\)
この記事では運動の3法則と束縛条件について解説しています。
特に、運動方程式に重点をおいています。
運動方程式の立て方や、利用の仕方を載せています。
また、空気抵抗についても解説しています。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.運動の3法則
運動の3法則は以下の3つになります。
①慣性の法則(運動の第1法則)
②運動の法則(運動の第2法則)
③作用反作用の法則(運動の第3法則)
これらについて解説していきます。
\(\bf{\underline{①慣性の法則(運動の第1法則)}}\)
物体は外から力を受けていないとき、あるいは受けていてもそれらがつりあっているとき、静止している物体は静止し続け、運動している物体は等速直線運動(速度が一定の運動)を続けます。
言い換えると、物体はその状態を維持しようとします。
※
質量が大きいほど、物体の状態は変わりにくい
質量についてはこちらも参考にしてください
→力のはたらきとつりあい
上記の性質を、\(\textcolor{red}{\bf{慣性の法則}}\)といいます。
\(\bf{\underline{②運動の法則(運動の第2法則)}}\)
力を受けている物体は、その力の向きに加速度を生じます。
その加速度の大きさは、力の大きさに比例し、物体の質量に反比例します。
これを、\(\textcolor{red}{\bf{運動の法則}}\)といいます。
上記から、質量を\(m\)、物体の受けている力を\(F\)、生じる加速度を\(a\)、比例定数を\(k\)とすると以下のようになります。
\(\displaystyle{a=k\frac{F}{m}}\)

上式において、比例定数\(k\)が\(1\)となるように決められた力の単位が\(N\)(ニュートン)となります。
\(1N\)は、質量\(1kg\)の物体に\(1m/s^2\)の大きさの加速度を生じさせる力の大きさとなります。
上記が力の定義です。
運動の法則(運動の第2法則)を、質量\(m[kg]\)、加速度\(\vec{a}[m/s^2]\)、力\(\vec{F}[N]\)で表すと、
\(\displaystyle{\textcolor{red}{m\vec{a}=\vec{F}}}\)
上式を、\(\textcolor{red}{\bf{運動方程式}}\)といいます。
“運動方程式”は、\(\textcolor{red}{\bf{動いている物体についての式}}\)になります。
また、”運動方程式”の右辺の\(\vec{F}\)は、物体にかかっている力の”合力”となります。
※
静止している物体
→つりあいの式を用いる
運動している物体
→運動方程式を用いる
加速度\(a\)は\(v-t\)グラフの傾きを表しているため、等速直線運動(速度が一定の運動)をしている物体については、\(a=0\)となります。(傾きが\(0\))。
また、物体にはたらいている力がつりあっているとき、合力が\(0\)なので運動方程式の右辺が\(0\)となります。
その結果、加速度\(a=0\)(\(v-t\)グラフの傾きが\(0\))となり、物体は等速直線運動をすることがわかります。
運動方程式は因果律を表しており、下図のような意味になります。

\(\bf{\underline{③作用反作用の法則(運動の第3法則)}}\)
2つの物体が、互いに力を及ぼしあうとき、作用と反作用は同一直線上にあり、逆向きで大きさが等しいです。
これを、\(\textcolor{red}{作用反作用の法則}\)といいます。
作用反作用の法則については、こちらで詳しく解説しています。
→力のはたらきとつりあい
2.運動方程式の利用
“運動方程式”は動いている物体に関する式になります。
動いている物体については、この運動方程式を立式し、\(v-t\)グラフを描いていきます。
この”運動方程式”の立て方について、解説していきます。
運動方程式の立て方は、以下のようになります。
①運動方程式を立てる物体について、かかっている力を図示する
②軸を設定する(\(x\)軸、\(y\)軸)
正の向きは、初速度が正となる方向または、物体が動く方向にとります。
(落下運動①で扱ったものと同じ)
③物体が受けている力を、設定した軸方向に分ける。
(力のベクトルを成分表示で考える)
※力の成分表示については、こちらも参考にしてください。
→力とベクトル
④それぞれの方向について、運動方程式を立てる
上記のことを、実際に例を用いてみていきます。
例)糸につながれて上昇している物体
(物体の質量を\(m\)、重力加速度を\(g\)とする)
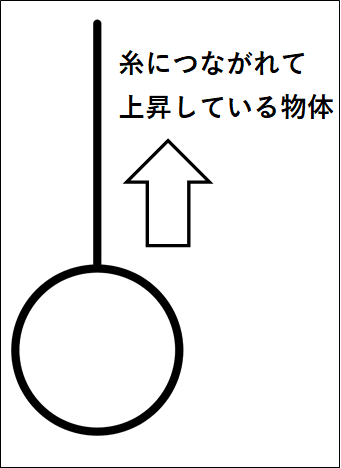
\(\bf{\underline{①かかっている力を図示する}}\)
まず、非接触力である”重力”が鉛直下向きにかかっています。
次に、物体の表面をなでまわすと糸とあたるので、この部分に張力\(T\)がかかっています。
向きは、糸が抜ける方向である鉛直上向きです。
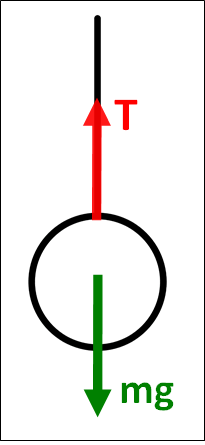
\(\bf{\underline{②軸を設定する}}\)
物体は上昇しているので、鉛直上向きを正として\(y\)軸を設定します。
今回は、力が上下方向にしかかかっていないので\(y\)軸の設定だけします。
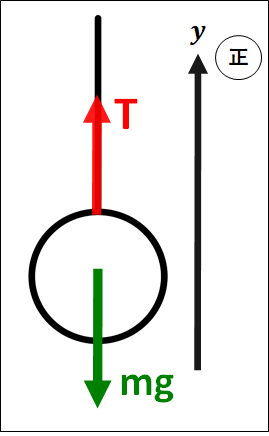
\(\bf{\underline{③力を軸方向に分ける}}\)
今回は、重力と張力のどちらも\(y\)軸に沿っているので、力を分ける必要はありません。
もしも、\(x\)軸や\(y\)軸に沿っていない力があれば、力を\(x\)軸や\(y\)軸方向にわけます。
これは、運動方程式を\(x\)軸方向や\(y\)軸方向について立式するためです。
(ベクトルそのものは扱いにくいので、\(x\)成分や\(y\)成分で考える)
\(\bf{\underline{④運動方程式を立てる}}\)
図示した力と設定した軸から、張力\(T\)は正の向き、重力\(mg\)は負の向きになります。
このことから、\(y\)軸方向の加速度を\(a_y\)とすると、運動方程式は
\(\displaystyle{\begin{eqnarray}ma_y&=&(+T)+(-mg)\\\\&=&T-mg\end{eqnarray}}\)
となります。

※
今回は、左右方向(\(x\)軸方向)には力がはたらいていないので運動方程式を立てる必要は無いのですが、立てると以下のようになります。
\(x\)軸方向の加速度を\(a_x\)とします。
\(\displaystyle{ma_x=0}\)
今回左右方向には力がかかっていないので、その合力は\(0\)となります。
上式から、加速度\(a_x\)は\(0\)となり(両辺\(m\)で割った)、\(x\)軸方向の\(v-t\)グラフの傾きは\(0\)となります(\(x\)軸と平行になる)。
今回左右方向には動いていないので、はじめの速度は\(0\)なので、\(x\)軸方向の\(v-t\)グラフは、\(x\)軸と重なることになります。
上記のように運動方程式を立てた後は、加速度(\(v-t\)グラフの傾き)を求めるなどして、\(v-t\)グラフを描き、その結果から問題を解いていくことになります。
この運動方程式がわかると、落下運動①でしていたことが分かります。
→落下運動①
空中で物体にかかっている力は重力\(mg\)のみになります。
(空気抵抗は無視する)
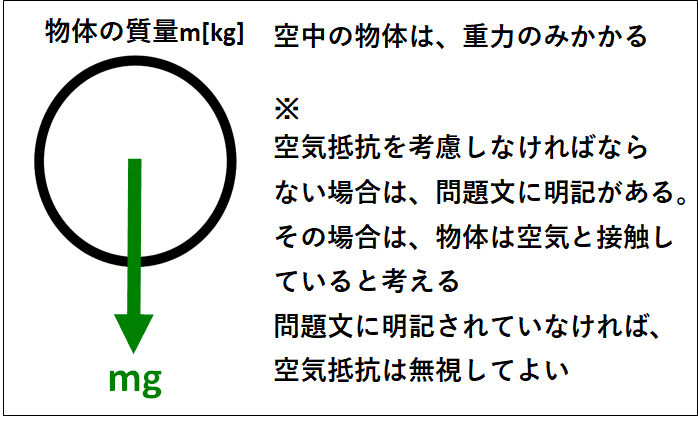
この場合、鉛直上向きを正とした場合の\(y\)軸方向の運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma_y=-mg\\\\\Leftrightarrow&&a_y=-g\end{eqnarray}}\)
となり、\(v-t\)グラフの傾きは\(-g\)となります。
これにより、グラフの傾きは右下がりになっていました。
鉛直下向きを正とした場合の\(y\)軸方向の運動方程式は
\(\displaystyle{\begin{eqnarray}&&ma_y=mg\\\\\Leftrightarrow&&a_y=g\end{eqnarray}}\)
となり、\(v-t\)グラフの傾きは\(g\)となります。
これにより、グラフの傾きは右上がりになっていました。
落下運動①で扱っていた、\(v-t\)グラフの傾きである重力加速度とその正負は、上記の運動方程式を立て、加速度について解いた結果を用いていました。
3.束縛条件
\(\textcolor{red}{\bf{束縛条件}}\)とは、”2つ以上の物体が連動して動くときの幾何学的条件”となります。
具体例をみてもらったほうが、わかりやすいと思います。
例1)
静止していた物体\(A\)と物体\(B\)が接した状態で、\(A\)に右向きに力を加えて動かしたとき。
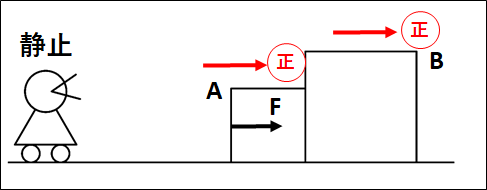
上図の状態では、\(A\)は力\(F\)を加えられて右向きに動きます。
\(B\)は、\(A\)に押されて右向きに動きます。
このとき、\(A\)と\(B\)の間にどのような関係があるかをみていきます。
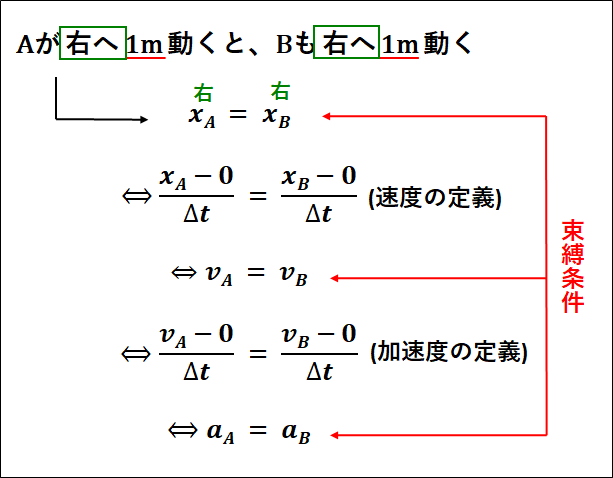
まず、\(A\)と\(B\)は接しているので、\(A\)が\(\textcolor{green}{\bf{右に}}\)\(\textcolor{red}{\bf{1m}}\)動くと、\(B\)も\(\textcolor{green}{\bf{右に}}\)\(\textcolor{red}{\bf{1m}}\)動きます。
このことから、\(A\)が動いた距離を\(x_A\)、\(B\)が動いた距離を\(x_B\)とすると、以下の式が成り立ちます。
\(x_A=x_B\)
また、速度の定義式を用いて、
(速度・加速度についてはこちら→変位・速度・加速度)
\(\displaystyle{\begin{eqnarray}x_A&=&x_B\\\\{\Leftrightarrow}\frac{x_A-0}{\Delta{t}}&=&\frac{x_B-0}{\Delta{t}}\\\\{\Leftrightarrow}v_A&=&v_B\end{eqnarray}}\)
これより、\(A\)が右向きに動く速さと、\(B\)が右向きに動く速さが同じことがわかりました。
さらに、加速度の定義式を用いて、
\(\displaystyle{\begin{eqnarray}v_A&=&v_B\\\\{\Leftrightarrow}\frac{v_A-0}{\Delta{t}}&=&\frac{v_B-0}{\Delta{t}}\\\\{\Leftrightarrow}a_A&=&a_B\end{eqnarray}}\)
これより、\(A\)が右向きに生じる加速度の大きさと、\(B\)が右向きに生じる加速度の大きさが同じであることがわかりました。
以上のことから、束縛条件は
\(\displaystyle{\begin{eqnarray}x_A&=&x_B\\\\{\Leftrightarrow}v_A&=&v_B\\\\{\Leftrightarrow}a_A&=&a_B\end{eqnarray}}\)
となります。
※
微分を用いて書くと、
\(\displaystyle{\begin{eqnarray}x_A&=&x_B\\\\{\Leftrightarrow}\frac{dx_A}{dt}&=&\frac{dx_B}{dt}\\\\{\Leftrightarrow}v_A&=&v_B\\\\{\Leftrightarrow}\frac{dv_A}{dt}&=&\frac{dv_B}{dt}\\\\{\Leftrightarrow}a_A&=&a_B\end{eqnarray}}\)
となります。
例2)
滑車にかけられた糸の先端につながれている物体\(A\)、\(B\)について。
\(A\)が下向きに動いているとき。
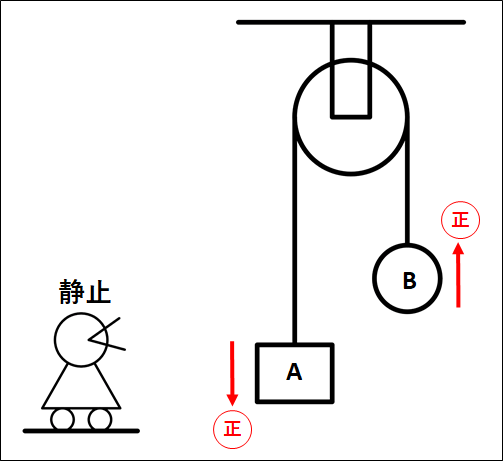
こちらについては、\(A\)と\(B\)は糸を介して繋がっており、糸は滑車にかけられているので、\(A\)が\(\textcolor{green}{\bf{下に}}\)\(\textcolor{red}{\bf{1m}}\)動くと、\(B\)は\(\textcolor{green}{\bf{上に}}\)\(\textcolor{red}{\bf{1m}}\)動きます。
それぞれの物体について、\(A\)を下向き正、\(B\)を上向きに正とします。
\(A\)が下向きに動いた距離を\(x_{A下}\)、\(B\)が上向きに動いた距離を\(x_{B上}\)とすると、動いた距離は同じになるので
\(\displaystyle{x_{A下}=x_{B上}}\)
となります。
動いた距離が同じなので、例1)のときと同様に、速度の定義と加速度の定義を用いていくと、
(\(x_{A下}=x_{B上}\)の両辺を\(t\)で微分していくと)
\(\displaystyle{\begin{eqnarray}x_{A下}&=&x_{B上}\\\\{\Leftrightarrow}v_{A下}&=&v_{B上}\\\\{\Leftrightarrow}a_{A下}&=&a_{B上}\end{eqnarray}}\)
となります。

これが、束縛条件となります。
例2)においては、それぞれの大きさは同じですが、向きが異なることに注意してください。
4.空気抵抗と終端速度
\(\bf{空気抵抗}\)は、空気中を運動する物体に対して、運動の向きとは”逆向き”にはたらく力になります。
速さが大きくない範囲では、空気抵抗の大きさは、速さに比例することが知られています。
よって、比例定数\(k\)を用いると空気抵抗の大きさは
\(\textcolor{green}{kv}\)
と表されます。
ここで、自由落下する質量\(m\)の物体を考えます。
落下する物体は、速度が大きくなっていきますが、速度が大きくなると空気抵抗も大きくなっていきます。
そのため、最終的に空気抵抗と重力がつりあい、速度は一定となります。
このときの速度\(v_f\)を\(\textcolor{red}{\bf{終端速度}}\)といいます。
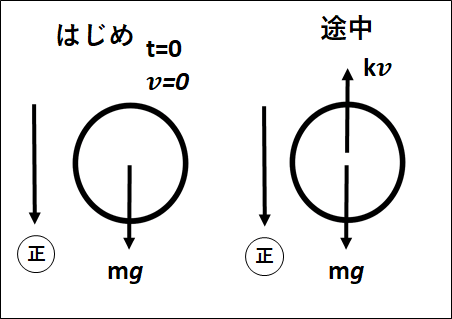
上図から、途中の運動方程式は
\(ma=mg-kv\cdots①\)
となります。
\(\bf{○はじめのとき}\)
はじめの状態では、\(v=0\)なので\(①\)に代入して
\(\displaystyle{\begin{eqnarray}ma&=&mg-k・0\\\\{\Leftrightarrow}ma&=&mg\\\\{\Leftrightarrow}a&=&g\end{eqnarray}}\)
よって、はじめの加速度は\(g\)となります。
\(\bf{○重力と空気抵抗がつりあったとき}\)
最終的には、重力と空気抵抗がつりあって速度は一定となるので\(a=0\)となります。(\(v-t\)グラフの傾きが\(0\))
このつりあったときの速度(終端速度)を\(v_f\)とすると、\(①\)から
\(\displaystyle{\begin{eqnarray}m・0&=&mg-kv_f\\\\{\Leftrightarrow}kv_f&=&mg\\\\{\Leftrightarrow}v_f&=&\frac{mg}{k}\end{eqnarray}}\)
これより、終端速度は
\(\displaystyle{v_f=\frac{mg}{k}}\)
となります。
\(v-t\)グラフは以下のようになります。
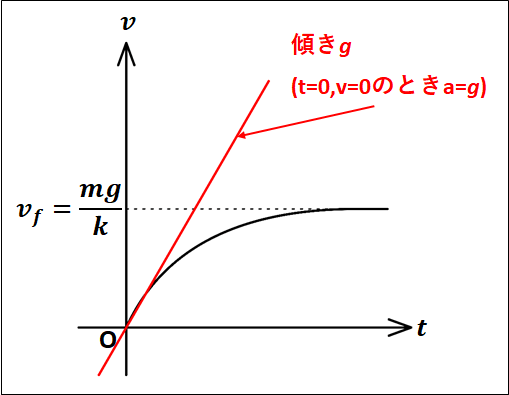
グラフ中に描いた傾き\(g\)は、\(t=0\)におけるグラフの接線になります。
また、グラフの各点における加速度は、その点における接線の傾きとなります。
グラフから、時間が経つにつれ速度が一定になっていく様子が分かると思います。
また、速さが小さいときの空気抵抗の大きさは\(kv\)と\(v\)に比例していましたが、速さが大きくなると\(kv^2\)と\(v^2\)に比例したものになります。
こちらも、終端速度を求めるだけならば、最終的に\(a=0\)となることを利用して、運動方程式から求めることができます。
\(\displaystyle{\begin{eqnarray}m・0&=&mg-k{v_f}^2\\\\{\Leftrightarrow}k{v_f}^2&=&mg\\\\{\Leftrightarrow}{v_f}^2&=&\frac{mg}{k}\end{eqnarray}}\)
から、
\(\displaystyle{v_f=\sqrt{\frac{mg}{k}}}\)
となります。
※
このグラフの関数を求めるには…
加速度の定義式から、
\(\displaystyle{a=\frac{dv}{dt}}\)
これより、途中の運動方程式は
\(\displaystyle{\begin{eqnarray}ma&=&mg-kv\\\\{\Leftrightarrow}m\frac{dv}{dt}&=&mg-kv\\\\{\Leftrightarrow}\frac{dv}{dt}&=&g-\frac{k}{m}v\end{eqnarray}}\)
となります。
上式は、「1階線形微分方程式」と呼ばれるもので、これを解くことで\(v\)と\(t\)の関係式を導くことができます。
興味があれば、調べてみてください。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


