投稿日:
【高校物理】v-tグラフと等加速度直線運動【v-tグラフ】【等加速度直線運動】
\(\require{color}\)
\(\require{cancel}\)
\(v-t\)グラフとは、速度\(v\)と時間\(t\)の関係を表したグラフになります。
このグラフには様々な情報が含まれており、問題を解くうえで活用するので、しっかりと理解しておく必要があります。
主に、\(v-t\)グラフの解説や書き方、読み取りの方法を解説しています。
補足解説と練習問題の記事はこちらです
→v-tグラフと等加速度直線運動(補足解説と練習問題)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.v-tグラフ
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{{\bf{・加速度}}a[m/s^2]}\)
\(\textcolor{red}{→v-t{\bf{グラフの傾き}}}\)
\(\textcolor{red}{{\bf{・変位}}x[m]}\)
\(\textcolor{red}{→v-t{\bf{グラフの面積}}}\)
\(v-t\)グラフとは、速度\(v[m/s]\)と時間\(t[s]\)の関係を表したグラフです。
様々な情報が含まれており、問題を解く際に用いるのでしっかりと活用できるようにしなければなりません。
\(v-t\)グラフは基本的にはじめとあとの情報で構成されており、これを図示したものとなります。
例えば、
はじめ:\(t=t_{\bf{はじめ}}(=0)\)のとき\(v=v_{\bf{はじめ}}\)
あと:\(t=t_{\bf{あと}}\)のとき\(v=v_{\bf{あと}}\)
のとき、\(v-t\)グラフは下図のようになります。
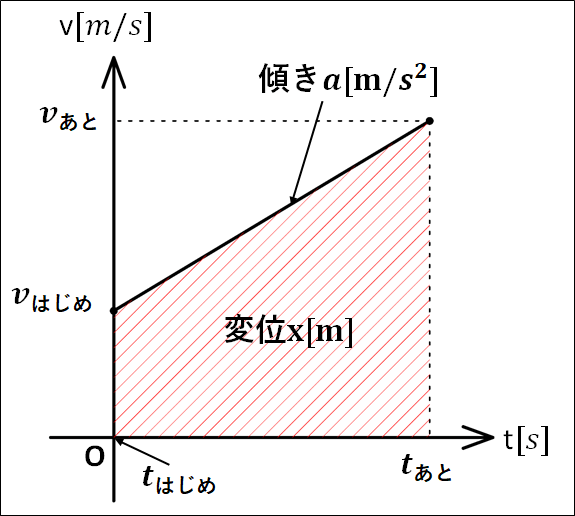
\(\bf{\underline{加速度について}}\)
加速度\(a[m/s^2]\):
→\(v-t\)グラフの傾きを表す
定義式は
\(\displaystyle{a[m/s^2]=\frac{v_{\bf{あと}}-v_{\bf{はじめ}}[m/s]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}\)
\(a=0\)のとき、\(x\)軸と平行
\(a\gt0\)のとき、右上がり
\(a\lt0\)のとき、右下がり
\(\bf{\underline{変位について}}\)
変位\(x[m]\):
→\(v-t\)グラフの面積
\(v\gt0\)(\(t\)軸より上の面積)のとき正
\(v\lt0\)(\(t\)軸より下の面積)のとき負
変位は、正の面積と負の面積の和になります。
移動距離は、面積の大きさの合計となるので、
\({\bf{(正の面積)}}+|{\bf{(負の面積)}}|\)
で表されます。
\(\underline{v_{\bf{はじめ}}{\bf{について}}}\)
\(v_{\bf{はじめ}}\)を\(\textcolor{red}{\bf{初速度}}\)といい、\(t=0\)のときの速度を意味します。
変位・速度・加速度については、こちらの記事も参考にしてください。
→変位・速度・加速度
\(v-t\)グラフから\(x-t\)グラフを書く際は、変位\(x\)が\(v-t\)グラフの面積であることを利用します。
\(v-t\)グラフから\(a-t\)グラフを書く際は、加速度\(a\)が\(v-t\)グラフの傾きであることを利用します。
これらについては、別記事の練習問題のほうで具体的にみていきたいと思います。
特に、\(v-t\)グラフの傾きが直線(加速度の値が一定)のものを\(\textcolor{red}{\bf{等加速度直線運動}}\)といいます。
※\(v-t\)グラフの面積(変位\(x\)について)
少しの時間を\(dt[s]\)とすると、時間\(dt[s]\)の間の変位は
\(v[m/s]×dt[s]=vdt[m]\)
となります。
(\(m/s×s=m(メートル)\))
グラフでみてみると、
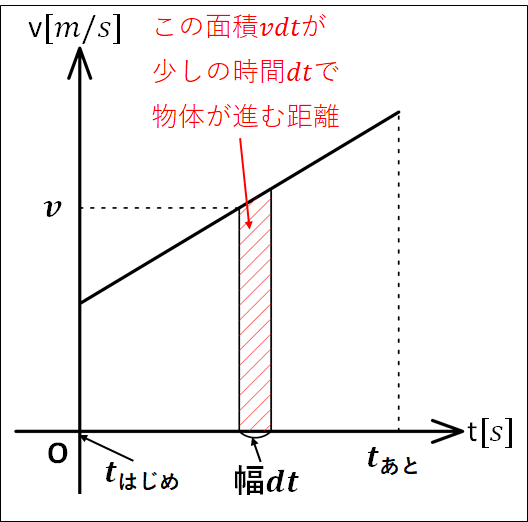
画像では、\(dt\)にはある程度の幅がありますが、実際には限りなく小さい幅であるとイメージしてください。
そうすると、赤色斜線部は画像では台形にみえますが、限りなく細くなっていき線(長方形)であるとみなせます。
なので、一瞬の時間\(dt\)の間の物体の変位は(縦×横)で\(vdt\)となります。
この面積を、\(t_{\bf{はじめ}}\)から\(t_{\bf{あと}}\)まで足していきます。
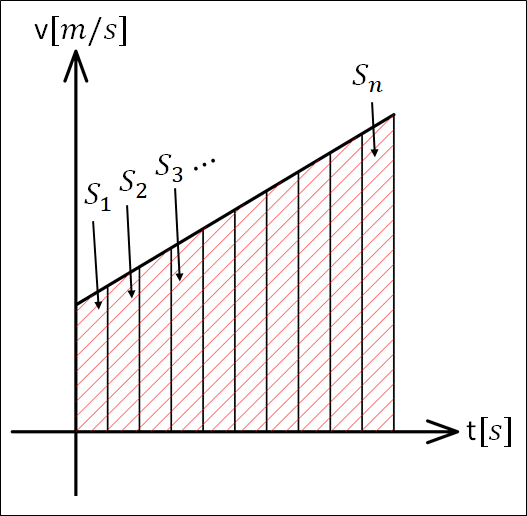
各部分の面積を\(S_{1},S_{2},S_{3}{\cdots}S_{n}\)とすると、\(t_{\bf{はじめ}}\)から\(t_{\bf{あと}}\)までの変位は
\(S_{1}+S_{2}+S{3}+{\cdots}+S_{n}\)
となります。
よって、全体の面積が変位\(x\)となります。
※補足
積分を考える
微小時間\(dt\)の間の変位\(x[m]\)は\(vdt[m]\)。
これを\(t_{\bf{はじめ}}\)から\(t_{\bf{あと}}\)までなめらかに足して(積分して)
\(\displaystyle{x[m]=\int_{t_{\bf{はじめ}}}^{t_{\bf{あと}}}vdt}\)
となります。
グラフと面積については、こちらも参考にしてください
→積分法
→積分法の応用
→よく使う積分の考え方と微積公式まとめ
2.v-tグラフの読み取り
練習問題を通して、\(v-t\)グラフの読み取り練習をします。
使う知識は、
・加速度は\(v-t\)グラフの傾きを表している
・加速度\(a[m/s^2]\)の定義は
\(\displaystyle{a=\frac{v_{\bf{あと}}-v_{\bf{はじめ}}}{t_{\bf{あと}}-t_{\bf{はじめ}}}}\)
・\(v-t\)グラフの面積が変位\(x\)を表している
です。
\(\bf{[問題1]}\)
下図の\(v-t\)グラフのように物体が等加速度直線運動をしているとき、
(\(1)\)加速度の正負
(\(2)\)加速度
(\(3)\)時刻\(0\)秒から\(8.0\)秒までの移動距離
を求めよ。
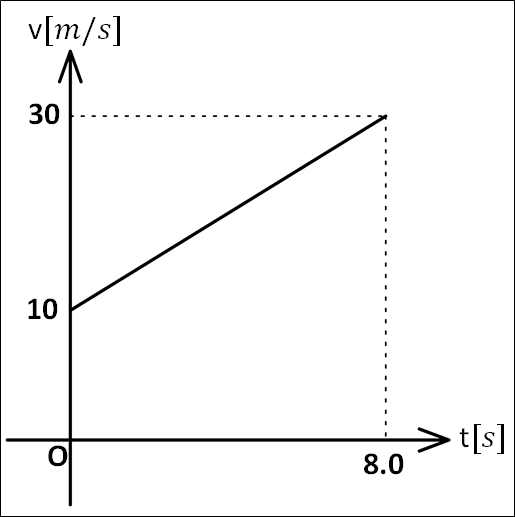
\(\bf{[問題1]の解答}\)
\((1)\)
グラフは右上がりの直線なので、加速度は正
\((2)\)
情報をまとめると
はじめ:\(t=0s\)で\(v=10m/s\)
あと:\(t=8.0s\)で\(v=30m/s\)
よって、加速度の定義式から
\(\displaystyle{\begin{eqnarray}a[m/s^2]&=&\frac{30m/s-10m/s}{8.0s-0s}\\\\&=&\frac{20m/s}{8.0s}\\\\&=&+2.5m/s^2\end{eqnarray}}\)
\((3)\)
グラフから、物体は常に正の方向に進んでいることがわかる。(グラフが常に\(t\)軸より上にあるため)
このことから、移動距離は\(v-t\)グラフの面積となるので、グラフの台形の面積を求めて
\(\displaystyle{\begin{eqnarray}&&(10m/s+30m/s)×8.0s×\frac{1}{2}\\\\=&&160m\\\\=&&1.6×10^2m\end{eqnarray}}\)
\(\bf{[問題2]}\)
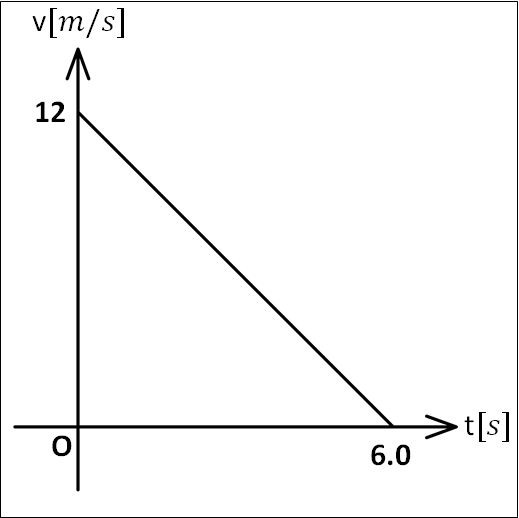
下図の\(v-t\)グラフのように物体が等加速度直線運動をしているとき、
\((1)\)加速度の正負
\((2)\)加速度
\((3)\)時刻(0秒)から\(6.0\)秒までの移動距離
を求めよ。
\(\bf{[問題2]の解答}\)
\((1)\)
グラフは右下がりの直線なので、加速度は正
\((2)\)
情報をまとめると
はじめ:\(t=0s\)で\(v=+12m/s\)
あと:\(t=6.0s\)で\(v=0m/s\)
よって、加速度の定義式から
\(\displaystyle{\begin{eqnarray}a[m/s^2]&=&\frac{0m/s-12m/s}{6.0s-0s}\\\\&=&\frac{-12m/s}{6.0s}\\\\&=&-2.0m/s^2\end{eqnarray}}\)
\((3)\)
グラフから、物体は常に正の方向に進んでいることがわかる。(グラフが常に\(t\)軸より上にあるため)
このことから、移動距離は\(v-t\)グラフの面積となるので、グラフの三角形の面積を求めて
\(\displaystyle{\begin{eqnarray}&&6.0s×12m/s×\frac{1}{2}\\\\=&&36m\end{eqnarray}}\)
3.v-tグラフの作成
与えられた情報から\(v-t\)グラフを作成するには、はじめの情報とあとの情報を把握して、グラフにプロットします。
等加速度直線運動ならば、グラフの傾きが直線(加速度の値が一定)となります。
注意する点としては、わからない部分は自分で文字でおきましょうということぐらいだと思います。
こちらも、練習問題を扱っていきます。
練習問題に使用するのは、加速度の定義式と\(v-t\)グラフの面積を求める式のみです。
\(\bf{[問題1]}\)
物体は等加速度直線運動をするとする。
静止している物体が、右向きの加速度\(1.0m/s^2\)で\(4.0\)秒間移動したとき、この間の変位はどちら向きに何\(m\)か。
\(\bf{[問題1]の解答}\)
物体は右向きに運動するので、右向きを正とします。
情報を整理します。
\(\textcolor{red}{\bf{静止している}}\)というのは、速度が\(0m/s\)ということです。
なので、はじめ(\(t=0s\))のとき\(v=0m/s\)という意味になります。
はじめとあとの情報を整理すると
はじめ:
\(t=0s\)で\(v=0m/s\)
あと:
\(t=4.0s\)で\(v=v_{\bf{あと}}[m/s]\)
あとの速度は分からないので、\(v_{\bf{あと}}\)としています。
また、右向きを正としているので、右向きの加速度の符合は\(+\)となります。
右向きの加速度\(1.0m/s^2\)→\(+1.0m/s^2\)
また、加速度は\(v-t\)グラフの傾きを表しています。
今、変位を求めるということなので、変位を\(x[m]\)としておきます。
変位は\(v-t\)グラフの面積となります。
以上のことをふまえて、\(v-t\)グラフを描くと、下図のようになります。
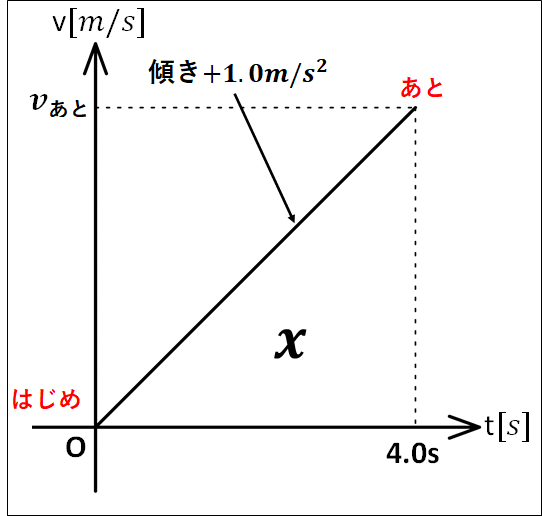
\(v-t\)グラフが描けたところで、問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&1.0m/s^2=\frac{v_{\bf{あと}}-0m/s}{4.0s-0s}\\\\\Leftrightarrow&&v_{\bf{あと}}=4.0m/s\cdots①\end{eqnarray}}\)
\(v-t\)グラフの面積(三角形の面積)から、変位\(x[m]\)は
\(\displaystyle{\begin{eqnarray}x[m]&=&4.0s×v_{\bf{あと}}×\frac{1}{2}\cdots②\end{eqnarray}}\)
\(①\)を\(②\)に代入して
\(\displaystyle{\begin{eqnarray}x[m]&=&4.0s×v_{\bf{あと}}×\frac{1}{2}\\\\&=&4.0s×4.0m/s×\frac{1}{2}\\\\&=&+8.0m\end{eqnarray}}\)
今右向きを正としているので、
\(\underline{{\bf{右向きに}}8.0m}\)
となります。
\(\bf{[問題2]}\)
物体は等加速度直線運動をするとする。
右向きの速さ\(3.0m/s\)で進んでいた物体が、右向きの加速度\(2.0m/s^2\)で\(5.0\)秒間移動したとき、この間の変位はどちら向きに何\(m\)か。
\(\bf{[問題2]の解答}\)
物体は右向きに運動するので、右向きを正とします。
情報を整理すると
はじめ:
\(t=0s\)のとき、右向きの速さ\(3.0m/s\)
→\(+3.0m/s\)(右向きを正としているので符合は\(+\))
あと:
\(t=5.0s\)のとき、\(v=v_{\bf{あと}}\)
右向きの加速度\(2.0m/s^2\)
→\(+2.0m/s^2\)(右向きを正としているので符合は\(+\))
これが、\(v-t\)グラフの傾きとなる。
変位\(x[m]\)は\(v-t\)グラフの面積
以上から\(v-t\)グラフを描くと、下図のようになります。
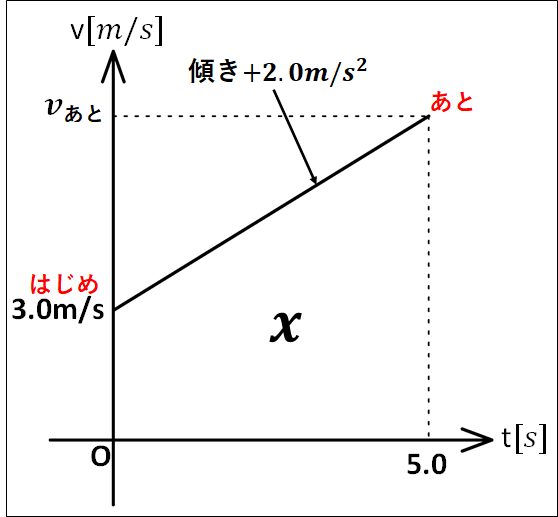
問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&2.0m/s^2=\frac{v_{\bf{あと}}-3.0m/s}{5.0s-0s}\\\\\Leftrightarrow&&v_{\bf{あと}}=13m/s\cdots①\end{eqnarray}}\)
\(v-t\)グラフの面積(台形の面積)から、変位\(x[m]\)は
\(\displaystyle{x[m]=(3.0m/s+v_{\bf{あと}})×5.0s×\frac{1}{2}\cdots②}\)
\(①\)を\(②\)に代入して、
\(\displaystyle{\begin{eqnarray}x[m]&=&(3.0m/s+v_{\bf{あと}})×5.0s×\frac{1}{2}\\\\&=&(3.0m/s+13m/s)×5.0s×\frac{1}{2}\\\\&=&+40m\end{eqnarray}}\)
今右向きを正としているので、
\(\underline{{\bf{右向きに}}40m}\)
となります。
\(\bf{[問題3]}\)
物体は等加速度直線運動をするとする。
静止していた物体が、右向きの加速度\(6.0m/s^2\)の運動をはじめ、右側に\(3.0m\)移動したとき、物体の速度はどちら向きに何\(m/s\)か。
\(\bf{[問題3]の解答}\)
物体は右向きに運動するので、右向きを正とします。
情報を整理すると
はじめ:
\(t=0s\)のとき、静止
→\(0m/s\)
あと:
\(t=t_{\bf{あと}}\)のとき、\(v=v_{\bf{あと}}\)
右向きの加速度\(6.0m/s^2\)
→\(+6.0m/s^2\)(右向きを正としているので符合は\(+\))
これが、\(v-t\)グラフの傾きとなる。
変位\(x[m]\)は\(v-t\)グラフの面積
以上から\(v-t\)グラフを描くと、下図のようになります。
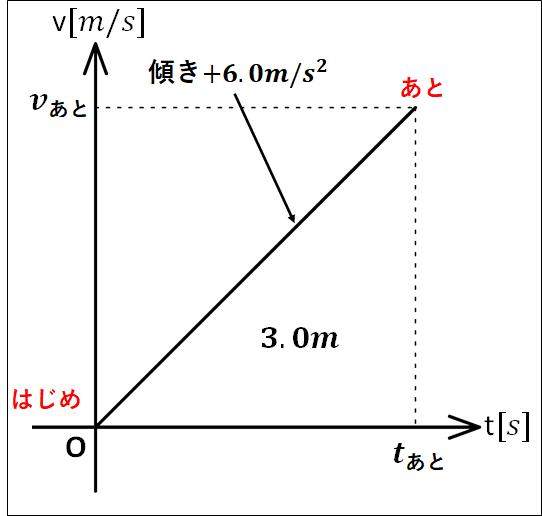
問題を解いていきます。
加速度の定義式から
\(\displaystyle{\begin{eqnarray}&&6.0m/s^2=\frac{v_{\bf{あと}}-0m/s}{t_{\bf{あと}}-0s}\\\\\Leftrightarrow&&v_{\bf{あと}}=6.0m/s^2×t_{\bf{あと}}\cdots①\end{eqnarray}}\)
\(v-t\)グラフの面積(三角形の面積)から、変位\(3.0[m]\)は
\(\displaystyle{\begin{eqnarray}&&3.0m=t_{\bf{あと}}×v_{\bf{あと}}×\frac{1}{2}\\\\\Leftrightarrow&&t_{\bf{あと}}=\frac{6m}{v_{\bf{あと}}}\cdots②\end{eqnarray}}\)
\(②\)を\(①\)に代入して、
\(\displaystyle{\begin{eqnarray}&&v_{\bf{あと}}=6.0m/s^2×\frac{6m}{v_{\bf{あと}}}\\\\\Leftrightarrow&&v_{\bf{あと}}^2=6.0^2m^2/s^2\end{eqnarray}}\)
\(v-t\)グラフから、\(v_{\bf{あと}}\gt0\)なので、\(v_{\bf{あと}}=+6.0m/s\)
今右向きを正としているので、
\(\underline{{\bf{右向きに}}6m/s}\)
となります。
この手の問題は、\(v-t\)グラフを描き、加速度の定義式と(v-t)グラフの面積の式を立式することで解くことができます。
4.等加速度直線運動
等加速度直線運動とは、これまでに説明したように\(v-t\)グラフが直線(加速度の値が一定)である物体の運動となります。
変位・速度・加速度の解説で、平均の加速度と瞬間の加速度の説明をしましたが、\(v-t\)グラフの傾きが一定のときにはこの2つの値は同じになります。
※
平均の加速度は、あととはじめの点を結んだ直線の傾きであるが、傾き一定のためどこをあと、はじめにしても傾きは同じになる。
一方、瞬間の加速度もグラフの傾きが一定であるため、どこの点をみても傾きは同じになる。
等加速度直線運動には、公式と呼ばれるものが存在します。
これを\(v-t\)グラフから導出していきましょう。
(個人的には、加速度の定義式と面積の式で問題が解けるので、覚える必要はないと思いますが…)
\(\bf{[等加速度直線運動の公式]}\)
\(v=v_0+at\cdots①\)
\(\displaystyle{x=v_0t+\frac{1}{2}at^2\cdots②}\)
\(v^2-v_0^2=2ax\cdots③\)
上の公式中の\(v_0\)ははじめの速度、\(v\)はあとの速度のことです。
また、\(t_0\)ははじめの時間、\(t\)はあとの時間となります。
\((1)\)
加速度の定義式から、時刻\(t_0=0\)のとき\(①\)式を導く。
加速度の定義式は、
\(\displaystyle{a=\frac{v-v_0}{t-t_0}}\)
上式において、\(t_0=0\)のとき、
\(\displaystyle{\begin{eqnarray}&&a=\frac{v-v_0}{t-0}\\\\\Leftrightarrow&&at=v-v_0\\\\\Leftrightarrow&&v=v_0+at\end{eqnarray}}\)
となります。
\((2)\)
\(v-t\)グラフを用いて、\(v_0\gt0 , a\gt0\)のとき、\(②\)式を導く。
上記のとき、はじめの状態は\(t_0=0\)のとき\(v=v_0\gt0\)です。
そこから、加速度\(a\gt0\)なのでグラフは右上がりになります。
\(v-t\)グラフは以下のようになります。
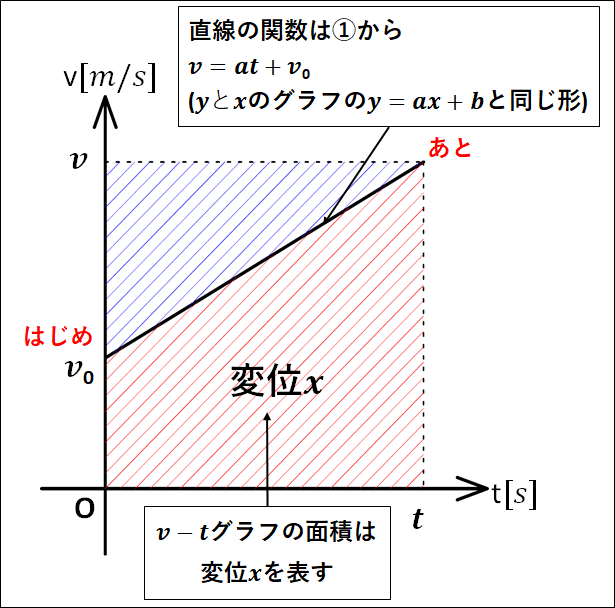
変位\(x\)は\(v-t\)グラフの面積なので、全体の四角形から青色の三角形の面積を引いて
\(\displaystyle{\begin{eqnarray}x&=&vt-\frac{1}{2}(v-v_0)t\\\\&=&\frac{1}{2}{2v-(v-v_0)}t\\\\&=&\frac{1}{2}(v+v_0)t\\\\&=&\frac{1}{2}(v_0+at+v_0)t (∵①)\\\\&=&\frac{1}{2}(2v_0+at)t\\\\&=&v_0t+\frac{1}{2}at^2\end{eqnarray}}\)
となります。
※台形の面積、
\(({\bf{上底}}+{\bf{下底}})×{\bf{高さ}}÷2\)
を用いると、変位\(x\)部分は台形なので
\(\displaystyle{\begin{eqnarray}x&=&(v_0+v)×t÷2\\\\&=&\frac{1}{2}(v_0+v)t\\\\&=&\frac{1}{2}(v_0+at+v_0)t (∵①)\\\\&=&v_0t+\frac{1}{2}at^2\end{eqnarray}}\)
となる。
\((3)\)
\(v-t\)グラフを用いて、\(v_0\gt0 , a\lt0\)のとき、\(②\)式を導く。
上記のとき、はじめの状態は\(t_0=0\)のとき\(v=v_0\gt0\)です。
そこから、加速度\(a\lt0\)なのでグラフは右下がりになります。
\(v-t\)グラフは以下のようになります。
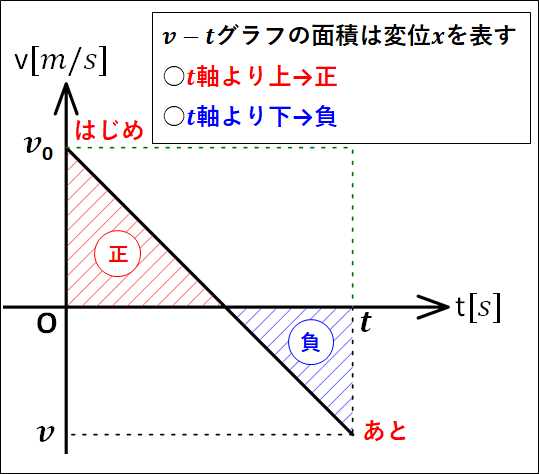
変位は、\(v-t\)グラフの面積であり、正の面積と負の面積の和となります。
したがって、正の面積から、負の面積の絶対値を引いたものとなります。
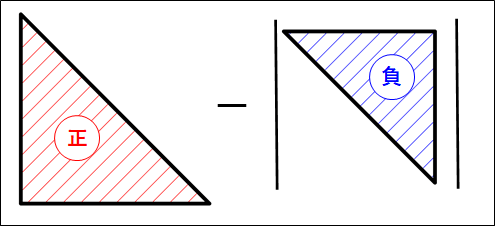
ここで、計算の工夫として、緑部分の面積を考えます。
緑部分の面積は共通なので、同じだけ足してから引いても計算結果は変わりません。
緑部分の面積を考慮すると、縦が\(v_0\)で横が\(t\)の長方形から、底辺が\(t\)で高さが\(v_0-v\)の三角形を引けばよいことが分かります。
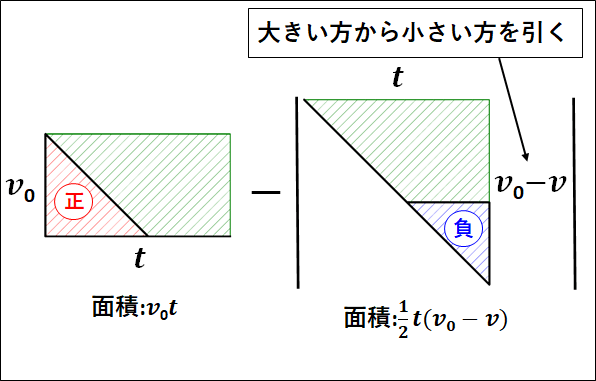
上記を計算すると、
\(\displaystyle{\begin{eqnarray}x=v_0t-\left|\frac{1}{2}t(v_0-v)\right|\end{eqnarray}}\)
ここで、\(t\)は正であり、\(v_0-v\)も正なので絶対値記号をとって
\(\displaystyle{\begin{eqnarray}x&=&v_0t-\left|\frac{1}{2}t(v_0-v)\right|\\\\&=&v_0t-\frac{1}{2}(v_0-v)t\\\\&=&\frac{1}{2}(2v_0-v_0+v)t\\\\&=&\frac{1}{2}(v_0+v)t\\\\&=&\frac{1}{2}(v_0+v_0+at)t (∵①)\\\\&=&\frac{1}{2}(2v_0+at)t\\\\&=&v_0t+\frac{1}{2}at^2\end{eqnarray}}\)
となります。
\((4)\)
\(v-t\)グラフを用いて、\(①\)式から\(t\)を消去して\(③\)式を導く。\((v_0\gt0 , a\gt0)\)
\(①\)式から
\(\displaystyle{\begin{eqnarray}&&v=v_0+at\\\\\Leftrightarrow&&v-v_0=at\\\\\Leftrightarrow&&t=\frac{v-v_0}{a}\end{eqnarray}}\)
\((2)\)の\(v-t\)グラフから、変位\(x\)は三角形の面積なので
\(\displaystyle{\begin{eqnarray}&&x=\frac{1}{2}(v+v_0)t\\\\\Leftrightarrow&&x=\frac{1}{2}(v+v_0)×\frac{v-v_0}{a} (∵t=\frac{v-v_0}{t})\\\\\Leftrightarrow&&x=\frac{1}{2a}(v+v_0)(v-v_0)\\\\\Leftrightarrow&&x=\frac{1}{2a}(v^2-v_0^2)\\\\\Leftrightarrow&&2ax=v^2-v_0^2\\\\\Leftrightarrow&&v^2-v_0^2=2ax\end{eqnarray}}\)
となります。
\((5)\)
\(v-t\)グラフを用いて、\(①\)式から\(t\)を消去して\(③\)式を導く。\((v_0\gt0 , a\lt0)\)
\((4)\)と同様にして、\(①\)式から
\(\displaystyle{t=\frac{v-v_0}{a}}\)
\((3)\)の\(v-t\)グラフ面積から、変位\(x\)を計算して
\(\displaystyle{\begin{eqnarray}&&x=\frac{1}{2}(v+v_0)t (←(4)と同じ式)\\\\\Leftrightarrow&&v^2-v_0^2=2at\end{eqnarray}}\)
となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


