投稿日:
【高校物理】変位・速度・加速度(補足解説と問題の解き方)【変位】【速度】【加速度】【練習問題】
\(\require{color}\)
\(\require{cancel}\)
変位・速度・加速度の記事で解説した内容の補足解説と練習問題となります。
実際に問題を解く際には、解説した内容をどのように用いるのかに注目して読み進めてください。
また、変位・速度・加速度の記事で解説していなかった補足内容があれば、この記事に載せています。
「変位・速度・加速度」の記事はこちらです。
→変位・速度・加速度
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.単位の変換と平均の速さ
\(\underline{\bf{<目的>}}\)
・単位の扱いに慣れる
単位についてはこちらも参考にしてください
→単位の計算や換算(変換)方法
\(\bf{\underline{[問題]}}\)
新幹線が駅間距離517kmある京都駅から東京駅を移動することを考える。
京都駅を7:00に出発し、東京駅に9:12に到着するとするとき、この京都駅-東京駅間における新幹線の平均の速さはいくらになるか?
単位をkm/hとm/sで答えよ。
\(\underline{\bf{[解答]}}\)
km/hのhは、1時間という意味です。
よって、この場合は単位時間(1時間)あたりに平均何km進むかを答えるというものになります。
はじめの状況と、あとの状況をまとめると
はじめ:7:00に京都駅(0km)
あと:9:12に東京駅(517km)
また、9:12の12の単位は分なのでこれも時間になおして表示すると
\(\displaystyle{9\frac{12}{60}}\)
となります。
何km/hかを聞かれているので、距離の単位はkm、時間の単位はh(時)として平均の速度の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\overline{V}=\frac{x_{あと}-x_{はじめ}}{t_{あと}-t_{はじめ}}\end{eqnarray}}}\)
から
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{517km-0km}{9\frac{12}{60}h-7h}\\\\&=&\frac{517km}{2\frac{12}{60}h}\\\\&=&\frac{517km}{\frac{132}{60}h}\end{eqnarray}}\)
ここで、
\(\textcolor{red}{\bf{方法1}}\)
→分母を先に計算する
先ほどの式から
\(\displaystyle{\begin{eqnarray}\frac{517km}{\frac{132}{60}h}&=&\frac{517km}{2.2h}\\\\&=&235km/h\end{eqnarray}}\)
より、
\(\underline{235km/h}\)(有効数字3桁)
となります。
※有効数字についてはこちら
→有効数字
\(\textcolor{red}{\bf{方法1}}\)
→分子分母に60を掛ける
同様にして、計算途中の式から、
\(\displaystyle{\begin{eqnarray}\frac{517km}{\frac{132}{60}h}&=&\frac{517km×60}{\frac{132}{60}h×60}\\\\&=&\frac{517×60km}{132h}\\\\&=&235km/h\end{eqnarray}}\)
より、
\(\underline{235km/h}\)(有効数字3桁)
となります。
次に、分速m/sを求めていきます。
こちらも、単位の換算については「単位の計算や換算(変換)方法」で扱っているので、目を通してみてください。
\(\displaystyle{\textcolor{green}{\begin{eqnarray}k&=&1000\\\\&=&10^3\end{eqnarray}}}\)
\(\displaystyle{\textcolor{green}{\begin{eqnarray}h&=&3600s\end{eqnarray}}}\)
なので、先ほどの平均の速度の式から、
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{517\textcolor{green}{k}m}{2\frac{12}{60}\textcolor{green}{h}}\\\\&=&\frac{517×\textcolor{green}{10^3}m}{\frac{132}{60}×\textcolor{green}{3600s}}\\\\&=&\frac{517×10^3m}{132×60s}\\\\&=&65.2777{\cdots}m/s\end{eqnarray}}\)
より、
\(\underline{65.3m/s}\)(有効数字3桁)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・小中の復習→単位計算をしっかりする
・計算結果を有効数字でかえす
ちなみに、京都駅から東京駅までの間、新幹線の速さは常に一定ではありません。
途中途中で速くなったり、遅くなったりしています。
新幹線だと想像しにくいかもしれませんが、自動車だとスピードのメーターが常に一定の値を指していることはなく、また信号でとまった際などには速さは0となります。
出発するときも、いきなり60km/hがでているわけではなく、0km/hから徐々に速さが大きくなっていき60km/hに至ります。
平均の速さというのは、上記のように瞬間瞬間での速さではなく、ある地点からある地点までもしも一定の速さで進んだらどれだけの速さになるか?という値になります。
別記事で解説しているv-tグラフを用いると、京都駅から東京駅までの瞬間瞬間の速さはばらばらですが、同じv-tグラフの面積になるように平らにしたものが平均の速度となります。
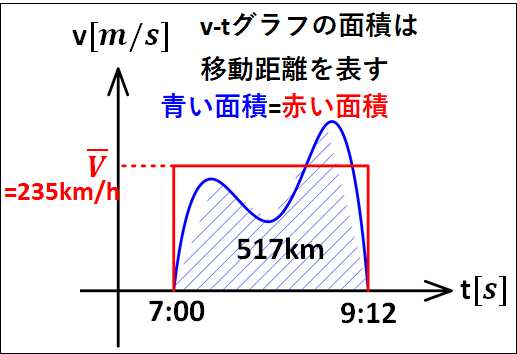
※v-tグラフについてはこちら
→v-tグラフと等加速度直線運動
2.平均の速さと瞬間の速さ
\(\underline{\bf{[問題]}}\)
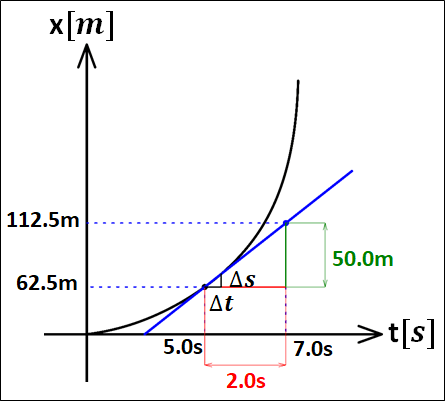
次のx-tグラフにおける、時刻5.0sから7.0sまでの平均の速さと、時刻5.0sにおける瞬間の速さを求めよ。
※x-tグラフは時間と位置の関係を表したグラフ。
y-tグラフやs-tグラフということもある
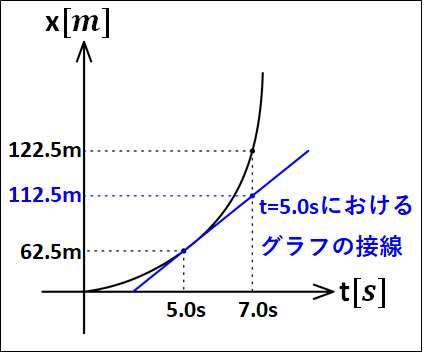
\(\underline{\bf{[解答]}}\)
○平均の速さ
はじめとあとの点を考えると、以下のようになります。
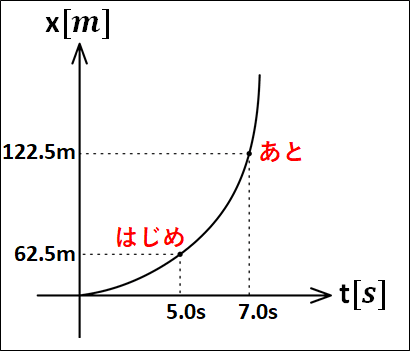
こちらも、はじめとあとの状況をまとめると
はじめ:5.0sで62.5m
あと:7.0sで122.5m
よって、平均の速度の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\overline{V}=\frac{x_{あと}-x_{はじめ}}{t_{あと}-t_{はじめ}}\end{eqnarray}}}\)
から、
\(\displaystyle{\begin{eqnarray}\overline{V}&=&\frac{122.5m-62.5m}{7.0s-5.0s}\\\\&=&\frac{60.0m}{2.0s}\\\\&=&30m/s\end{eqnarray}}\)
よって、平均の速さについては、
\(\underline{30m/s}\)(有効数字2桁)
となります。

\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・x-t(y-t,s-t)グラフの意味
・有効数字
○瞬間の速さ
時刻5.0sにおける瞬間の速さは、この時刻における接線の傾きとなります。
瞬間の速さを考えるために、時刻5.0sの点からほんの少しだけの時間\(\Delta{t}\)経った点を考えます。
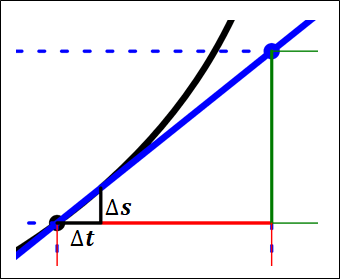
このときの時刻は、(5.0s+\(\Delta{t})\)となります。
またこの時の物体の位置を\(\Delta{s}\)とすると、位置\(x[m]\)は(62.5m+\(\Delta{s})\)となります。
これより、時刻5.0sを”はじめ”、ほんの少しの時間\(\Delta{t}\)だけ経ったあとの状態を”あと”とすると、
はじめ:5.0sのとき62.5m
あと:5.0s+\(\Delta{t}\)のとき62.5m+\(\Delta{s}\)
となります。
このときの速さを考えると、定義式から
\(\displaystyle{\begin{eqnarray}V&=&\frac{(62.5+\Delta{s})-62.5m}{(5.0s+\Delta{t})-5.0s}\\\\&=&\frac{\Delta{s}}{\Delta{t}}\end{eqnarray}}\)
これは、接線の傾きを表します。
また、グラフから下図の直角三角形が相似であることがわかります。
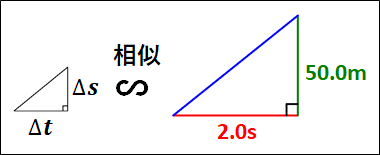
上図2つの直角三角形は相似なので、斜辺の傾きは同じとなります。
よって、
\(\displaystyle{\begin{eqnarray}V&=&\frac{\Delta{s}}{\Delta{t}}\\\\&=&\frac{50.0m}{2.0s}\\\\&=&25m/s\end{eqnarray}}\)
以上から、時刻5.0sにおける瞬間の速さは
\(\underline{25m/s}\)(有効数字2桁)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・微小量の扱い方
→ほんの少しだけの変化を考える
(数学でいう微分係数)
※微分係数についてはこちらも参考にしてください
→微分係数と導関数
3.変位と移動距離と平均の速度
\(\underline{\bf{[問題]}}\)
ある物体が点Oから同一直線上を右に向かって40秒間で80m移動した後、左に向かって20秒間で20m移動した。
点Oを出発してから60秒間での、この物体の「変位・移動距離・平均の速度」を求めよ。
\(\underline{\bf{[解答]}}\)
問題文中に「平均の\(\textcolor{red}{\bf{速度}}\)」を求めよとあります。
速度とは「\(\textcolor{red}{\bf{ベクトル}}\)」(向きと大きさがある)なので、以下の設定をする必要があります。
\(\textcolor{red}{\bf{・軸の設定}}\)
\(\textcolor{red}{\bf{・原点と正の向きの設定}}\)
今回は、点Oを出発してからの話なので「原点」を点O、はじめ右向きに移動するので右向きを正としておきます。
図示すると下図のようになります。
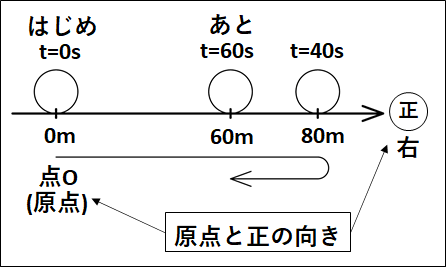
○変位
変位の定義式
\(\displaystyle{\textcolor{green}{\overrightarrow{x}={\bf{(あとの座標)-(はじめの座標)}}}}\)
から、
\(\displaystyle{\begin{eqnarray}\overrightarrow{x}&=&(60m)-(0m)\\\\&=&+60m\end{eqnarray}}\)
軸は右向きを正としているので、変位の符合(+)は翻訳すると右向きという意味になります。
よって変位は
\(\underline{{\bf{右向きに}}60m}\)
となります。
○移動距離
移動した距離は、右向きに80m移動した後、左向きに20m移動しているので
\(80m+20m=100m\)
よって移動距離は
\(\underline{100m}\)
となります。
○平均の速度
これまでと同様に、平均の速度\(\vec{V}\)の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\vec{V}=\frac{{\bf{(あとの座標)}}-{\bf{(はじめの座標)}}}{{\bf{(あとの時間)}}-{\bf{(はじめの時間)}}}\end{eqnarray}}}\)
から、
\(\displaystyle{\begin{eqnarray}\vec{V}&=&\frac{60m-0m}{60s-0s}\\\\&=&\frac{+60m}{60s}\\\\&=&+1.0m/s\end{eqnarray}}\)
こちらも変位と同様に、右向きを正としているので速度の符合は翻訳すると右向きであることを意味しています。
よって平均の速度は
\(\underline{{\bf{右向きに}}1.0m/s}\)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・ベクトルの処理の仕方
→図と数式で扱う
4.平均の加速度
同一直線上を左右に走っている人について、4.0s間で
i) 右向きに2.0m/sから右向きに6.0m/s
ii) 右向きに2.0m/sから左向きに4.0m/s
にそれぞれ変化した場合の平均の加速度を求めよ。
※
この問題は、v-tグラフの練習問題でも扱います。
\(\underline{\bf{[解答]}}\)
加速度の定義式
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\vec{a}=\frac{\bf{(あとの速度)-(はじめの速度)}}{\bf{(あとの時間)-(はじめの時間)}}\end{eqnarray}}}\)
を用います。
また、加速度もベクトルなので軸を設定する必要があるので、右向きを正としておきます。
i)
図示すると下図のようになります。
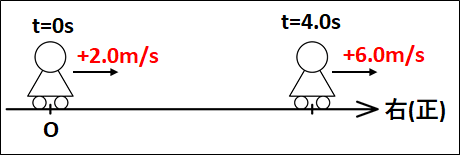
はじめとあとの時間と速度をまとめてみます。
右向きを正としているので
はじめ:t=0でv=+2.0m/s
あと:t=4.0sでv=+6.0m/s
これと、加速度の定義式から
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\frac{(+6.0m/s)-(+2.0m/s)}{4.0s-0s}\\\\&=&\frac{+4.0m/s}{4.0s}\\\\&=&+1.0m/s^2\end{eqnarray}}\)
右向きを正としているので加速度の符合は翻訳すると右向きであることを意味しています。
よって平均の加速度は
\(\underline{{\bf{右向きに}}1.0m/s^2}\)
となります。
ii)
図示すると下図のようになります。
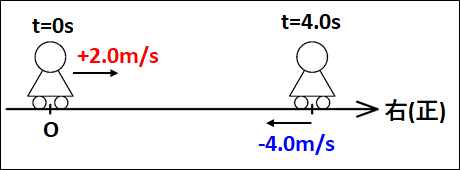
はじめとあとの時間と速度をまとめてみます。
右向きを正としているので
はじめ:t=0でv=+2.0m/s
あと:t=4.0sでv=-4.0m/s
これと、加速度の定義式から
\(\displaystyle{\begin{eqnarray}\vec{a}&=&\frac{(-4.0m/s)-(+2.0m/s)}{4.0s-0s}\\\\&=&\frac{-6.0m/s}{4.0s}\\\\&=&-1.5m/s^2\end{eqnarray}}\)
右向きを正としているので加速度の符合は翻訳すると左向きであることを意味しています。
よって平均の加速度は
\(\underline{{\bf{左向きに}}1.5m/s^2}\)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・速度・加速度の扱い
→ベクトル
→向きと大きさがある
→1.軸の設定
2.原点と正の方向の設定
・加速度の定義
5.変位と速度
\(\underline{\bf{[問題]}}\)
x-y平面上を等速直線運動をしている物体が、点A(4.0m,11m)から点B(12m,2.0m)に3.0sで移動したときの変位と速度の成分(x成分とy成分)を求めよ。
\(\underline{\bf{[解答]}}\)
○変位
変位はベクトルとなるので、図示すると下図のようになります。
※ベクトルについてはこちら
→ベクトルの演算と成分表示
→力とベクトル
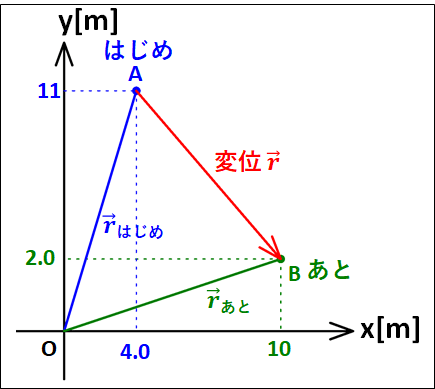
図中の\(\textcolor{blue}{\vec{r}_{はじめ}}\)と\(\textcolor{green}{\vec{r}_{あと}}\)を”位置ベクトル”といいます。
この位置ベクトルを用いると、変位ベクトル\(\textcolor{red}{\vec{r}}\)は
\(\displaystyle{\textcolor{red}{\vec{r}}=\textcolor{green}{\vec{r}_{あと}}-\textcolor{blue}{\vec{r}_{はじめ}}}\)
のように、
(あとの位置ベクトル)-(はじめの位置ベクトル)
で表すことができます。
それぞれの位置ベクトルを成分表示すると、
\(\displaystyle{\textcolor{blue}{\vec{r}_{はじめ}=\left(\begin{array}{l}4.0m\\11m\end{array}\right)}}\)
\(\displaystyle{\textcolor{green}{\vec{r}_{あと}=\left(\begin{array}{l}10m\\2.0m\end{array}\right)}}\)
これより、変位ベクトル\(\textcolor{red}{\vec{r}}\)は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{r}}&=&\textcolor{green}{\vec{r}_{あと}}-\textcolor{blue}{\vec{r}_{はじめ}}\\\\&=&\textcolor{green}{\left(\begin{array}{l}10m\\2.0m\end{array}\right)}-\textcolor{blue}{\left(\begin{array}{l}4.0m\\11m\end{array}\right)}\\\\&=&\textcolor{red}{\left(\begin{array}{l}10m-4.0m\\2.0m-11m\end{array}\right)}\\\\&=&\textcolor{red}{\left(\begin{array}{r}6.0m\\-9.0m\end{array}\right)}\end{eqnarray}}\)
以上から
変位のx成分
\(\underline{6.0m}\)
変位のy成分
\(\underline{-9.0m}\)
となります。
※
これまでと同様にx成分とy成分を別々で考えると
x軸方向について
はじめのx座標:4.0m
あとのx座標:10m
から、x軸方向の変位は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{x}}&=&\textcolor{green}{10m}-\textcolor{blue}{4.0m}\\\\&=&\textcolor{red}{+6.0m}\end{eqnarray}}\)
同様にしてy軸方向についても考えると
はじめのy座標:11m
あとのy座標:2.0m
から、x軸方向の変位は
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{y}}&=&\textcolor{green}{2.0m}-\textcolor{blue}{11m}\\\\&=&\textcolor{red}{-9.0m}\end{eqnarray}}\)
となります。
○速度
速度の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{速度}}\vec{v}&=&\frac{{\bf{変位}}\vec{r}}{\Delta{t}}\\\\\\&=&\frac{\left(\begin{array}{l}6.0m\\-9.0m\end{array}\right)}{3.0s}\\\\\\&=&\left(\begin{array}{l}+2.0m/s\\-3.0m/s\end{array}\right)\end{eqnarray}}\)
以上から
速度のx成分
\(\underline{+2.0m/s}\)
速度のy成分
\(\underline{-3.0m/s}\)
となります。
※
x成分とy成分を別々で考えると
x軸方向について
\(\vec{x}=+6.0m\)
より、x軸方向の速度\(v_x\)は
\(\displaystyle{\begin{eqnarray}v_x&=&\frac{\vec{x}}{\Delta{t}}\\\\&=&\frac{+6.0m}{3.0s}\\\\&=&+2.0m/s\end{eqnarray}}\)
y軸方向について
\(\vec{x}=-9.0m\)
より、y軸方向の速度\(v_y\)は
\(\displaystyle{\begin{eqnarray}v_y&=&\frac{\vec{y}}{\Delta{t}}\\\\&=&\frac{-9.0m}{3.0s}\\\\&=&-3.0m/s\end{eqnarray}}\)
となります。
ちなみに加速度の定義は
\(\displaystyle{{\bf{加速度}}\vec{a}=\frac{{\bf{速度}}\vec{v}}{\Delta{t}}}\)
です。
6.平均の速度
\(\underline{\bf{[問題]}}\)
点Aから東方向と45°の角度をなす北向きに物体を転がしたところ、下図のような軌道を描いて、4.0s後に点Aから80m離れた点Bを東方向と45°の角度をなして南向きに通り過ぎた。
このときの、AB間の平均の速度を求めよ。
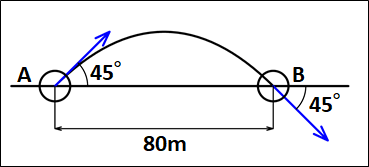
\(\underline{\bf{[解答]}}\)
変位と速度の定義に忠実にみていきます。
点Aを原点とするx-y座標をとると、点Aと点Bの座標は下図のようになります。
(東向き、北向きを正とする)
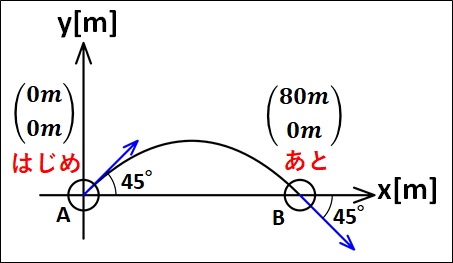
変位\(\vec{r}\)を求めると、これまでと同様に変位の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{変位}}\vec{r}&=&\left(\begin{array}{l}80m\\0m\end{array}\right)-\left(\begin{array}{l}0m\\0m\end{array}\right)\\\\&=&\left(\begin{array}{l}80m\\0m\end{array}\right)\end{eqnarray}}\)
変位が求まったので、速度の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{速度}}\vec{v}&=&\frac{{\bf{変位}}\vec{r}}{\Delta{t}}\\\\\\&=&\frac{\left(\begin{array}{l}80m\\0m\end{array}\right)}{4.0s}\\\\\\&=&\left(\begin{array}{l}20m/s\\0m/s\end{array}\right)\end{eqnarray}}\)
以上から、東向きと北向きを正ととっているので、成分をみてみると
\(\underline{{\bf{東向きに}}20m/s^2}\)
\(\underline{{\bf{北向きに}}0m/s^2}\)
となります。
\(\underline{\textcolor{red}{\bf{○ポイント}}}\)
・変位は”あと”と”はじめ”だけで決まる。
途中のルートは関係なし。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

関連記事
→変位・速度・加速度

