投稿日:
【高校物理】力とベクトル【力】【ベクトル】
\(\require{color}\)
\(\require{cancel}\)
力とは、物体の状態を変化させる原因となるものとなります。
これまでに、変位や速度、加速度がベクトルであると述べてきましたが、この力もベクトルとなります。
この記事では、基本的なベクトルの扱い方や、力の合成、分解について解説していきます。
補足解説と練習問題の記事はこちらです
→力とベクトル(補足解説と練習問題)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.力とは
静止している物体に力を加えると物体は動き出します。
また、動いている物体に力を加えると、物体の速さや運動の向きが変わります。
上記のように、力とは物体の状態(静止しているor運動している、速さ、運動の向きなど)を変化させる原因となるものとなります。
また、力は速度や加速度と同様に向きと大きさをもつベクトルとなります。
向きは矢印の向きで、大きさは矢印の長さで表現します。
(ベクトルについては、こちらも参考にしてください→ベクトルの演算と成分表示)
これから物理で必要なベクトルについて解説していきますが、ベクトルは数学で扱うので、厳密な定義や扱い方は数学の方で学んでください。
以下のような\(x-y\)座標上のベクトルを考えます。
赤色の矢印を\(\textcolor{red}{\vec{F_1}}\)(エフワンベクトル)とします。
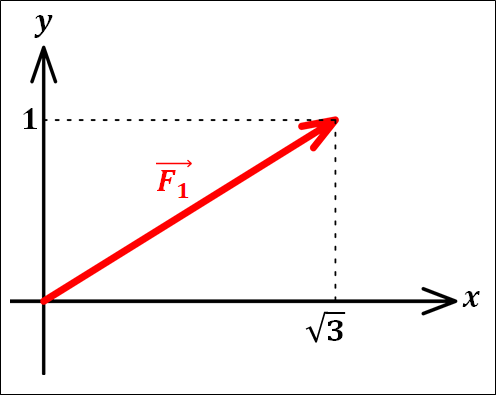
\(\textcolor{red}{\vec{F_1}}\)の向きは、図中の矢印の向きになります。
ちなみに、図中の直角三角形に注目すると、三角関数から
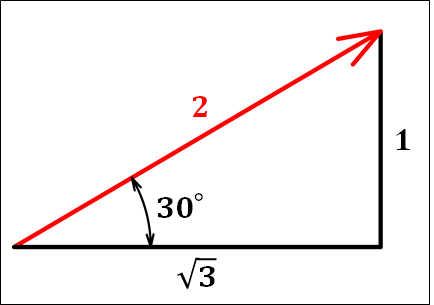
となるので、\(x\)軸と\(30°\)の角をなす方向であることが分かります。
(三角関数については、こちらも参考にしてください→三角関数の定義と関係式)
\(\textcolor{red}{\vec{F_1}}\)の大きさ\(\textcolor{red}{|\vec{F_1}|}\)は矢印の長さになります。
こちらも先ほどの直角三角形の図をみると、大きさは\(2\)となります。
(\(\textcolor{red}{|\vec{F_1}|=2}\)。三平方の定理から導ける)
また、矢印の先端から\(x\)軸、\(y\)軸上に垂直な線を引くと、\(\sqrt{3}\)、\(1\)と交わっています。
(\(x\)座標が\(\sqrt{3}\)。\(y\)座標が\(1\)。)
この\(x\)座標と\(y\)座標の値をそれぞれ\(\textcolor{red}{\vec{F_1}}\)の\(x\)成分、\(y\)成分といいます。
なので、\(\textcolor{red}{\vec{F_1}}\)の\(x\)成分は\(\sqrt{3}\)、\(y\)成分は\(1\)となります。
ベクトルの成分表示はいろいろありますが、物理では
\(\displaystyle{\textcolor{red}{\vec{F}}=\left(\begin{eqnarray}&&x\bf{成分}\\&&y\bf{成分}\end{eqnarray} \right)}\)
という、縦に並べた表記が有効です。
例で扱った\(\textcolor{red}{\vec{F_1}}\)で表記すると
\(\displaystyle{\textcolor{red}{\vec{F_1}}=\left(\begin{eqnarray}&&\sqrt{3}\\&& 1\end{eqnarray}\right)}\)
となります。
他の表記としては、
\((x,y)=(\sqrt{3},1)\)
や
\(\displaystyle{\left\{\begin{eqnarray}&&x=\sqrt{3}\\&&y=1\end{eqnarray}\right.}\)
などがあります。
2.力の合成
力はベクトルなので、ベクトルの加法のように計算することができます。
力の合成(ベクトルの合成)は、2つのベクトルを2辺とする平行四辺形を描いて行うことができます。
また、合成した力を”合力”といいます。
下図で説明していきます。
\(\textcolor{blue}{\vec{F_1}}\)と\(\textcolor{blue}{\vec{F_2}}\)の合力\(\textcolor{red}{\vec{F}}\)を、平行四辺形を描いて求めてみます。
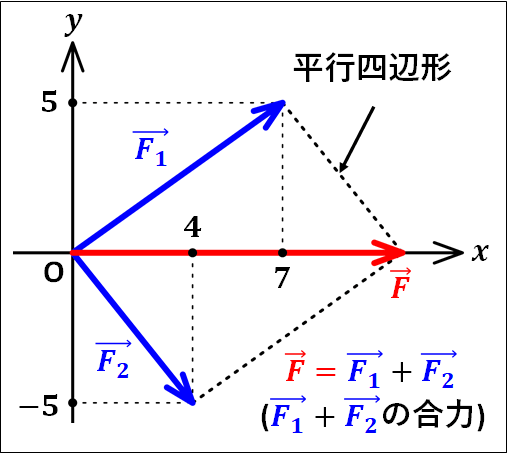
↓
ベクトルは平行移動させてもよいので、\(\textcolor{blue}{\vec{F_1}}\)だけ進んだところから、\(\textcolor{blue}{\vec{F_2}}\)だけ進んだベクトルであると考えることもできます。
↓
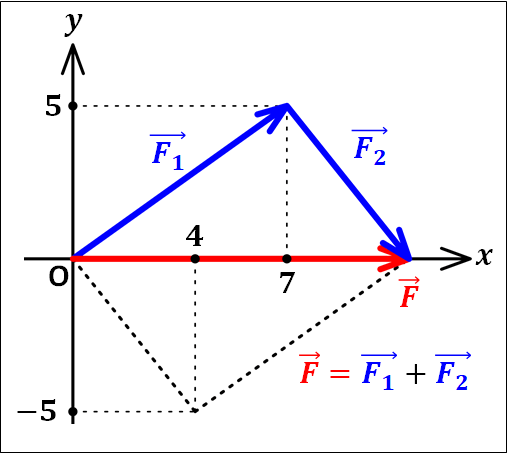
上図のように、平行四辺形を描いて矢印の始まりの点と平行四辺形の対角の点を結んだものが合力となります。
今回は図示する上で2つの力を扱いましたが、力はいくつでも、それぞれ任意の(すきな)2力の合成を続けていくことで、合力を求めていくことができます。
例えば\(\vec{F_1}\)と\(\vec{F_2}\)と\(\vec{F_3}\)の合力を図示する場合、まずは\(\vec{F_1}\)と\(\vec{F_2}\)の合力を図示し(この合力を\(\vec{F_{12}}\)とする)、そのあと\(\vec{F_{12}}\)と\(\vec{F_3}\)の合力を図示することで3力の合力を図示することができます。
次に成分を考えていきます。
図から
\(\displaystyle{\textcolor{blue}{\vec{F_1}=\left(\begin{eqnarray}&&7\\&&5\end{eqnarray}\right)}}\)
\(\displaystyle{\textcolor{blue}{\vec{F_2}=\left(\begin{eqnarray}&& 4\\&&-5\end{eqnarray}\right)}}\)
なので、\(\textcolor{blue}{\vec{F_1}}\)と\(\textcolor{blue}{\vec{F_2}}\)の合力\(\textcolor{red}{\vec{F}}\)の成分は、
\(\displaystyle{\begin{eqnarray}\textcolor{red}{\vec{F}}&=&\textcolor{blue}{\vec{F_1}+\vec{F_2}}\\\\&=&\textcolor{blue}{\left(\begin{eqnarray}&&7\\&&5\end{eqnarray}\right)}+\textcolor{blue}{\left(\begin{eqnarray}&& 4\\&&-5\end{eqnarray}\right)}\\\\&=&\textcolor{red}{\left(\begin{eqnarray}&&11\\&&0\end{eqnarray}\right)}\end{eqnarray}}\)
となります。
物理では力や速度でベクトルを扱いますが、斜め方向などのベクトルは扱いにくいので、成分での計算を行うことが多いです。
なので問題を解く中で、現在ベクトルそのものを扱っているのか、あるいはベクトルの成分を扱っているのかということに注意しておくと良いと思います。
3.力の分解
力の分解も平行四辺形を描くことで、任意の(すきな)2方向に分けることができます。
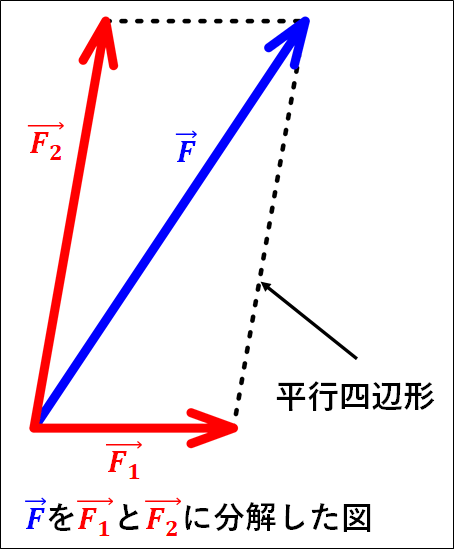
上図は、\(\textcolor{blue}{\vec{F}}\)を\(\textcolor{red}{\vec{F_1}}\)と\(\textcolor{red}{\vec{F_2}}\)に分解した図となります。
\(\textcolor{blue}{\vec{F}}\)を対角線とする平行四辺形を描くことで、この対角線であるベクトルを平行四辺形を形作る2辺に沿うベクトルに分解できます。
分解されたベクトルは、もとのベクトルと始点は一致しており、終点は平行四辺形の頂点となります。
また、ベクトルは平行移動させても変わらないので、\(\textcolor{red}{\vec{F_1}}\)と\(\textcolor{red}{\vec{F_2}}\)は下図のようにも表せます。
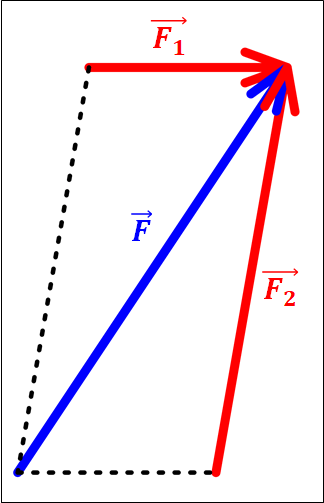
力の合成の部分でみた図に関して、
\(\vec{F_1}+\vec{F_2}=\vec{F}\)
は力の合成となりますが\(\vec{F_1}\)と\(\vec{F_2}\)は\(\vec{F}\)を2力に分解したものであるとみることもできます。
先ほど、物理では成分で扱うことが多いと述べましたが、ベクトルを成分で扱うために力の分解を行うことが多いです。
たいていは、水平方向と鉛直方向にベクトルを分解し、複数の力を水平方向の成分のみで考える、鉛直方向の成分のみで考える、とします。
なので、”ふつうは直交方向(直角に交わる方向)”にベクトルを分解します。
直角方向の分解に関して、特に\(\vec{F}\)を斜辺とする直角三角形の隣辺方向と対辺方向に分解するとき、隣辺と\(\vec{F}\)のなす角が\(\theta\)の際には、分解した2つのベクトルは\(\vec{F}\)の大きさ\(|\vec{F}|\)を用いて次のようになります。
(今回は\(x-y\)座標で表したので、隣辺方向のベクトル(\(x\)成分)を\(\vec{F_x}\)、対辺方向のベクトル(\(y\)成分)を\(\vec{F_y}\)としています。)
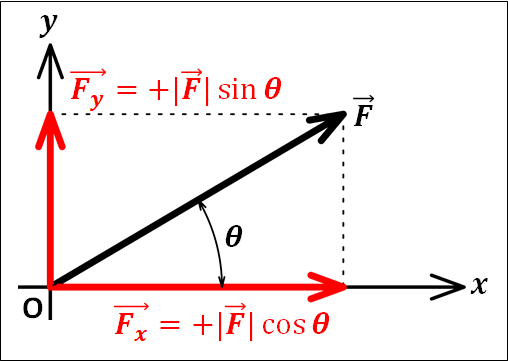
いま、分解したベクトルはそれぞれ\(x\)軸の正方向の向きと\(y\)軸の正方向の向きになるので、これらはどちらも正となります。
また、分解したベクトルを用いてもとのベクトル\(\vec{F}\)を成分表示すると
\(\displaystyle{\vec{F}=\left(\begin{eqnarray}&&\textcolor{red}{+|\vec{F}|\cos\theta}\\&&\textcolor{red}{+|\vec{F}|\sin\theta}\end{eqnarray}\right)}\)
となります。
上記の直角三角形を作ってベクトルを分解する際の覚え方を載せておきます。
(三角関数の定義から計算することもできますが、これぐらいは覚えておいてもいいと思います)
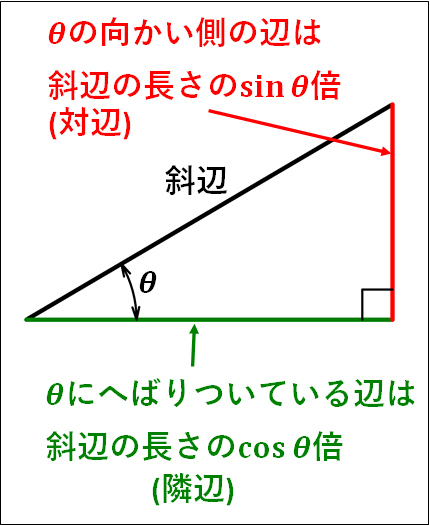
直角三角形を用いた各辺の長さとベクトルの分解については、こちらも参考にしてください。
→三角関数の定義と関係式
→練習問題1(三角関数の定義とグラフ)
→練習問題(ベクトル)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

関連記事
→力とベクトル(補足解説と練習問題)

