投稿日:
【高校物理】速度の合成と相対速度【合成速度】【相対速度】
\(\require{color}\)
\(\require{cancel}\)
速度はベクトルなので、ベクトルの加法や減法のように計算することができます。
また、相対速度とはあるものから見た別のあるものの速度のことになります。
例えば、地面からみた電車の中にいる人の速度などがこれになります。
相対速度は\(v-t\)グラフやベクトル図などで捉えることができますが、これらについて解説していきます。
補足解説と練習問題の記事はこちらです
→速度の合成と相対速度(補足解説と練習問題)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.速度の合成
速度は向きと大きさを持つベクトルなので、ベクトルの加法や減法のように計算することができます。
(ベクトルについては、こちらも参考にしてください→ベクトルの演算と成分表示)
例として、地面の上で静止している人と、動く床の上を歩く人を考えてみます。
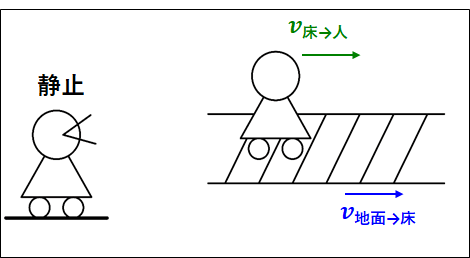
\(\textcolor{red}{\bf{静止している人(地面)から見て}}\)、床は速度\(\textcolor{blue}{v_{\bf{地面\to床}}}\)で動いているとし、床の上を歩く人は\(\textcolor{red}{\bf{床から見て}}\)速度\(\textcolor{green}{v_{\bf{床\to人}}}\)で歩いているとします。
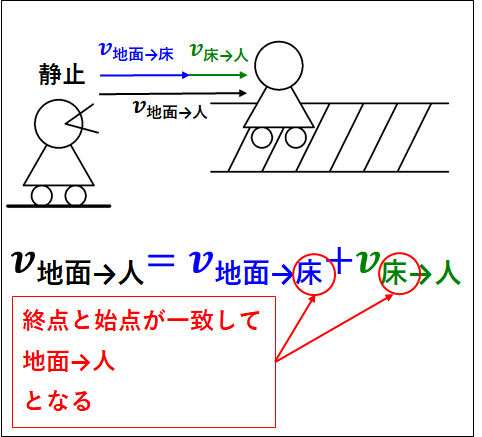
このとき、静止している人(地面)から見た床の上を歩いている人の速度を\(v_{\bf{地面\to人}}\)とすると、
\(v_{\bf{地面\to人}}=\textcolor{blue}{v_{\bf{地面\to床}}}+\textcolor{green}{v_{\bf{床\to人}}}\)
となります。
ベクトルの計算なので、イメージは以下のようになります。
例えば、
\(\textcolor{blue}{v_{\bf{地面\to床}}=+5.0m/s}\)
\(\textcolor{green}{v_{\bf{床\to人}}=+3.0m/s}\)
とすると、静止している人(地面)から見た床の上を歩いている人の速度\(v_{\bf{地面\to人}}\)は、
\(\displaystyle{\begin{eqnarray}v_{\bf{地面\to人}}&=&\textcolor{blue}{v_{\bf{地面\to床}}}+\textcolor{green}{v_{\bf{床\to人}}}\\\\&=&\textcolor{blue}{+5.0m/s}+\textcolor{green}{(+3.0m/s)}\\\\&=&+8.0m/s\end{eqnarray}}\)
となります。
このように、2つの速度を合わせた速度を求めることを、\(\textcolor{red}{\bf{速度の合成}}\)といい、この合わされた速度を\(\textcolor{red}{\bf{合成速度}}\)といいます。
2.相対速度
速度というと、一般的には静止した人(地面)から見た速度のことを指します。
これに対して、あるものから見た別のあるものの速度を\(\textcolor{red}{\bf{相対速度}}\)といいます。
例として、静止している人と車に乗っている人、電車に乗っている人を考えてみます。
静止している人(地面)から見た車の速度を\(\textcolor{blue}{v_{\bf{車}}}\)、静止している人(地面)から見た電車の速度を\(\textcolor{green}{v_{\bf{電車}}}\)とします。
このとき、車に乗った人から見た電車の速度を
\(\textcolor{red}{\bf{“車に対する電車の相対速度”}}\)
といいます。
※
\(A\)\(\textcolor{red}{\underline{\bf{に対する}}}\)\(B\)の相対速度
では分かりにくいので
→\(A\)\(\textcolor{red}{\underline{\bf{から見た}}}\)\(B\)の相対速度
と言い換えると分かりやすいと思います。
次のベクトル図と\(v-t\)グラフの活用で、実際にどのように相対速度が表されるのかをみていきます。
3.ベクトル図とv-tグラフの活用
先述の静止している人(地面)と、車、電車の速度の関係を、ベクトル図と\(v-t\)グラフで捉えてみます。
なお、車と電車は同一直線上を右向きに運動しているとし、\(\textcolor{blue}{v_{\bf{車}}}\lt\textcolor{green}{v_{\bf{電車}}}\)のときの車に対する(車から見た)電車の相対速度を考えます。
この、車に対する(車から見た)電車の相対速度を\(\textcolor{red}{v_{\bf{車\to電車}}}\)とします。
\(\bf{i)ベクトル図}\)
ベクトルは向きと大きさを持ち、向きを矢印の向きで、大きさを矢印の長さで表します。
(ベクトルについては、こちらも参考にしてください→ベクトルの演算と成分表示)
今回、車と電車は右向きに動いているので、右向きを正として図示すると下図のようになります。(原点は静止している人)
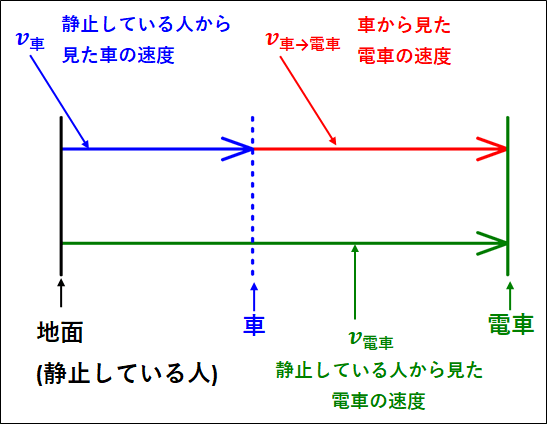
ベクトルの向きに注意しなけらばなりませんが、赤のベクトルは緑のベクトルから青のベクトルを引いたものとなるので、ベクトル図から赤色の車に対する(車から見た)電車の相対速度\(\textcolor{red}{v_{\bf{車\to電車}}}\)は、
\(\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}-\textcolor{blue}{v_{\bf{車}}}\)
となります。
または、図中の緑のベクトルが、青と赤のベクトルを足したものなので
\(\textcolor{blue}{v_{\bf{車}}}+\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}\)
から、\(\textcolor{blue}{v_{\bf{車}}}\)を右辺に移項させて
\(\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}-\textcolor{blue}{v_{\bf{車}}}\)
と考えると分かりやすいかもしれません。
\({\bf{ii)}}v-t{\bf{グラフ}}\)
\(v-t\)グラフは下図のようになります。\(v=0\)のときが静止している人(地面)の速度となります。
(\(v-t\)グラフについてはこちらも参考にしてください。→v-tグラフと等加速度直線運動)
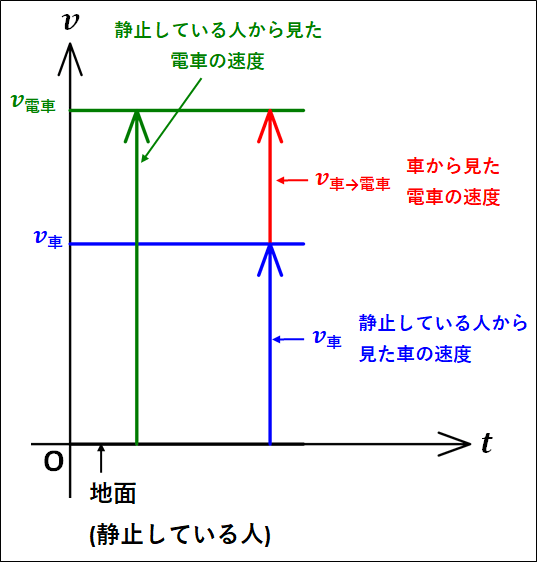
\(v-t\)グラフから、ベクトル図のときと同様にして車に対する(車から見た)電車の相対速度\(\textcolor{red}{v_{\bf{車\to電車}}}\)は
\(\textcolor{red}{v_{\bf{車\to電車}}}=\textcolor{green}{v_{\bf{電車}}}-\textcolor{blue}{v_{\bf{車}}}\)
となります。
\(v-t\)グラフは速度の正負は表現できるので、同一直線上を運動する物体については有効です。
(北と南、東と西方向など)
一方、速度ベクトルが同一直線上になく、斜め方向などの場合(例えば南と北東方向など)はベクトル図が有効となってきます。
こういった同一直線上にない速度をベクトル図で扱うには、簡単なベクトルの知識と三角関数の知識が必要となってきます。
(三角関数についてはこちらも参考にしてください→三角関数の定義と関係式)
一般に、\(A\)に対する\(B\)の相対速度\(v_{\bf{AB}}\)は、\(A\)の地面に対する速度を\(v_{\bf{A}}\)、\(B\)の地面に対する速度を\(v_{\bf{B}}\)とすると、
\(v_{\bf{AB}}=v_{\bf{B}}-v_{\bf{A}}\)(相手の速度-自分の速度)
で表されます。
上記式中の速度は、ベクトルなので成分計算をする場合は、符合も含めたものであることに注意しなければなりません。
例として、\(A\)さんが西に\(1.5m/s\)、\(B\)さんが東に\(1.0m/s\)で移動しているときを考えます。
西と東のどちらを正としてもよいですが、とりあえず東を正としておきます。
このとき、\(A\)さんと\(B\)さんのそれぞれの地面に対する速度を\(v_{\bf{A}}\)と\(v_{\bf{B}}\)とすると、東を正としているので
\(v_{\bf{A}}=-1.5m/s\)
\(v_{\bf{B}}=+1.0m/s\)
となります。
このときの、\(A\)さんに対する(\(A\)さんから見た)\(B\)さんの速度\(v_{\bf{AB}}\)は
\(\displaystyle{\begin{eqnarray}v_{\bf{AB}}&=&v_{\bf{B}}-v_{\bf{A}}\\\\&=&(+1.0m/s)-(-1.5m/s)\\\\&=&+2.5m/s\end{eqnarray}}\)
したがって、上記状況のとき\(A\)さんから見ると\(B\)さんは東へ\(2.5m/s\)の速さで移動しているように見えるということになります。(東を正としているので)
また、単に速度というときには、地面に対する速度のことを指しています。
\(\textcolor{red}{\bf{○ポイント}}\)
・\(A\)に対する\(B\)の相対速度は、\(A\)から見た\(B\)の相対速度と言い換えるとわかりやすい。
・\(\left\{\begin{eqnarray}&&\bf{○ベクトル図}\\&&\bf{○v-tグラフ}\end{eqnarray}\right.\bf{の利用}\)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


