投稿日:
【高校物理】変位・速度・加速度【変位】【速度】【加速度】
\(\require{color}\)
\(\require{cancel}\)
こちらでは、変位・速度・加速度の解説をしています。
また、速度と速さの違いや平均の速度と瞬間の速度の図形的意味、速度と加速度の定義式についても扱っています。
定義式については、問題を解くうえで何度も用いるので、しっかり覚えておく必要があります。
練習問題も別記事で用意しています。
問題を解くうえで、解説内容をどのように用いるのかや補足説明もしていますので、こちらの方にも目を通していただくようお願いします。
補足解説と練習問題の記事はこちらです。
→変位・速度・加速度(補足解説と練習問題)
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.変位と移動距離
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{\bf{・変位は”あと”と”はじめ”で決まる}}\)
\(\textcolor{red}{\bf{・変位と移動距離の違い}}\)
\(\textcolor{red}{\bf{変位}}\)とは、物体がどちら向きにどれだけ移動したかを表す量となります。
また、向き(符合)と大きさがあるので、ベクトルとなります。
(ベクトルについてはこちら→ベクトルの演算と成分表示)
変位がどのように表されるかというと、
\(\displaystyle{\bf{変位=(あとの座標)-(はじめの座標)}}\)
で表されます。
特に、\(x\)座標上の物体の場合、
\(\displaystyle{\textcolor{green}{\begin{eqnarray}{\bf{変位}}&=&{\bf{(あとの}}{x}{\bf{座標)-(はじめの}}{x}{\bf{座標)}}\\\\&=&x_{\bf{あと}}[m]-x_{\bf{はじめ}}[m]\\\\&=&\Delta{x}[m]\end{eqnarray}}}\)
となります。
\(\Delta\)は(あと-はじめ、変化量)という意味になります。
上記の式は、\(\textcolor{green}{\bf{変位の定義となる}}\)ので、覚えるようにしましょう。
また、物体の位置は時間によって変わるので、\(x\)は時間\(t\)の関数となります。(\(x(t)\)と書く)
ベクトルである変位に対して、移動距離とは、移動した距離の合計であり、向きを持ちません。
したがって、符合は必ず正となりスカラーとなります。
例)
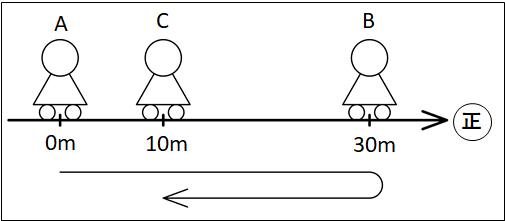
ある人が上図のように、\(A\)地点から\(B\)地点へと移動した後、\(C\)地点まで引き返したとします。(右向きを正とする)
このとき、変位は
(あとの\(x\)座標)=\(x_{\bf{あと}}\)=+\(10m\)
(はじめの\(x\)座標)=\(x_{\bf{はじめ}}\)=\(0m\)
なので、変位の定義から
\(\displaystyle{\begin{eqnarray}{\bf{変位}}\Delta{x}&=&x_{\bf{あと}}-x_{\bf{はじめ}}\\\\&=&+10m-0m\\\\&=&+10m\end{eqnarray}}\)
となります。
今、右向きを正としているので、\(+10m\)の符合\(+\)は、正の方向を表しています。
すなわち、右向きに\(10m\)という意味になります。
また、移動距離は\(A→B\)までで\(30m\)、\(B→C\)までで\(20m\)移動しているので、
\(30m+20m=50m\)
となります。
\(\textcolor{red}{\bf{○ポイント}}\)
\(\textcolor{red}{\bf{・変位は”あと”と”はじめ”で決まる}}\)
\(\textcolor{red}{\bf{・変位と移動距離の違い}}\)
2.速度と速さ
\(\textcolor{red}{\bf{速度}}\)とは単位時間あたりの変位で、こちらも向きと大きさをもつベクトルとなります。
単位時間の単位とは\(1\)という意味になります。
よって、単位時間というのは\(1\)秒や\(1\)分、\(1\)時間のことです。
※
\(1\)秒は\(1s\)とも書く。(\(s\)は\(second\)(秒)の頭文字)
\(1\)時間は\(1h\)とも書く。(\(h\)は\(hour\)(時間)の頭文字)
平均の速度\(\bar{v}\)の定義式は以下のようになります。
\(\displaystyle{\textcolor{green}{\bar{v}[m/s]=\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}}\)
上記は\(\textcolor{green}{\bf{平均の速度の定義となる}}\)ので、覚えるようにしましょう。
速度\(v\)は、\(velocity\)(速度)の頭文字です。
また、\(v\)の上についている\(-\)は平均という意味です。
定義式中の分子は\(x\)座標のあと-はじめなので変位となります。
分母は時間のあと-はじめになっています。
どちらもあと-はじめになっていることに注目しましょう。
あと-はじめ(変化量)という意味の\(\Delta\)(デルタ)を用いると、平均の速度の定義式は以下のようにも書けます。
\(\displaystyle{\begin{eqnarray}\bar{v}[m/s]&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{x}[m]}{\Delta{t}[s]}\end{eqnarray}}\)
速度\(v\)の単位は、距離\(m\)(メートル)を時間\(s\)(秒)で割っているので、\(m/s\)(メートル毎秒)となります。
(単位についてはこちら→単位の計算や換算(変換)方法)
向きと大きさをもつベクトルである速度に対して、この大きさにだけ注目したものが\(\textcolor{red}{\bf{速さ}}\)になります。
平均の速さを、平均の速度\(\bar{v}\)と絶対値記号を用いて表すと、
\({\bf{速さ}}=|\bar{v}|[m/s]\)
となります。
例)
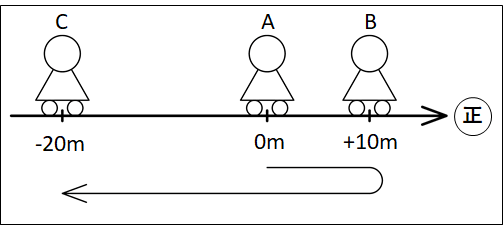
ある人が、上図のように(A→B→C)と(10)秒かけて移動したとします。
このときの、変位、移動距離、平均の速度、平均の速さを求めてみます。(右向きを正)
\(\bf(○変位)\)
はじめ(\(0\)秒のとき)、\(A\)地点にいるので\(x_{\bf{はじめ}}=0m\)
あと(\(10\)秒後)のとき\(C\)地点にいるので、\(x_{\bf{あと}}=-20m\)
以上より、変位の定義式から
\(\displaystyle{\begin{eqnarray}{\bf{変位}}&=&x_{\bf{あと}}-x_{\bf{はじめ}}\\\\&=&(-20m)-(0m)\\\\&=&-20m\end{eqnarray}}\)
となります。
今右向きを正としているので、求めた変位についている符合のマイナスは左向きを表しています。
よって、左向きに\(20m\)ということもできます。
\(\bf{○移動距離}\)
移動距離は、\(A→B\)までで\(10m\)、\(B→C\)までで\(30m\)移動しているので
\(10m+30m=40m\)
となります。
\(\bf{○平均の速度}\)
はじめの地点とあとの地点の情報をまとめてみます。
\(A\)地点にいるときがはじめで、\(B\)地点にいるときがあとです。
はじめ:\(0s\)のとき、\(0m\)
あと:\(10s\)のとき、\(-20m\)
この情報と、平均の速度の定義式から
\(\displaystyle{\begin{eqnarray}\bar{v}&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}}{t_{\bf{あと}}-t_{\bf{はじめ}}}\\\\&=&\frac{-20m-0m}{10s-0s}\\\\&=&\frac{-20m}{10s}\\\\&=&-2.0m/s\end{eqnarray}}\)
となります。
今右向きを正としているので、符合マイナスの意味は左向きという意味になります。
よって、左向きに\(2.0m/s\)ともいえます。
\(\bf{○速さ}\)
速さは、速度の大きさなので(向き=符合の情報はもたない)
\({\bf{速さ}}=|\bar{v}|=|-2.0m/s|=2.0m/s\)
となります。
3.平均の速度と瞬間の速度のグラフ(図形)的意味
\(\textcolor{red}{\bf{○ポイント}}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・平均の速度}\\\\x-t{\bf{グラフのはじめの点とあとの点を結んだ直線の傾き}}}}\end{eqnarray}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・瞬間の速度}\\\\x-t{\bf{グラフのある点における直線の傾き}}}}\end{eqnarray}\)
先ほどみたように、平均の速度\(\bar{v}\)は
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\bar{v}[m/s]&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{x}}{\Delta{t}}\end{eqnarray}}}\)
となります。
ここで、位置\(x[m]\)と時間\(t[s]\)の関係を表すグラフを考えてみます。(\(x-t\)グラフ)
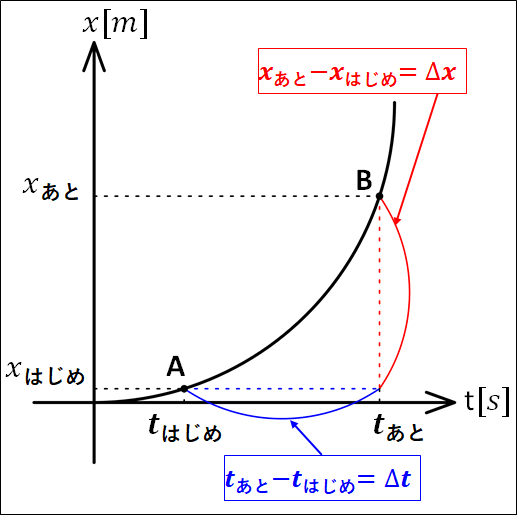
平均の速度\(\bar{v}\)は、
\(\displaystyle{\begin{eqnarray}\bar{v}[m/s]&=&\frac{\textcolor{red}{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}}{\textcolor{blue}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}\\\\&=&\frac{\textcolor{red}{\Delta{x}}}{\textcolor{blue}{\Delta{t}}}\\\\&=&\frac{\textcolor{red}{x{\bf{の変化量}}}}{\textcolor{blue}{t{\bf{の変化量}}}}\end{eqnarray}}\)
なので、これは点\(A\)と点\(B\)を結んだ直線の傾きとなります。
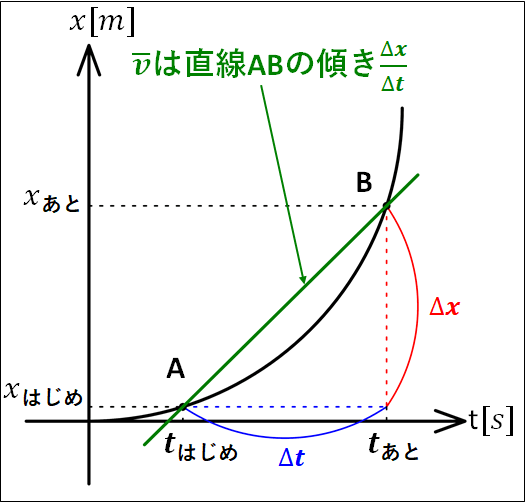
ここで、\(t_{\bf{あと}}\)を\(t_{\bf{はじめ}}\)に近づけていくと、\(x_{\bf{あと}}\)は\(x_{\bf{はじめ}}\)に近づいていきます。
このとき、直線\(AB\)の傾きも変化していきます。
瞬間の速度は、\(t_{\bf{あと}}\)を\(t_{\bf{はじめ}}\)に限りなく近づけたときの、接線の傾きになります。
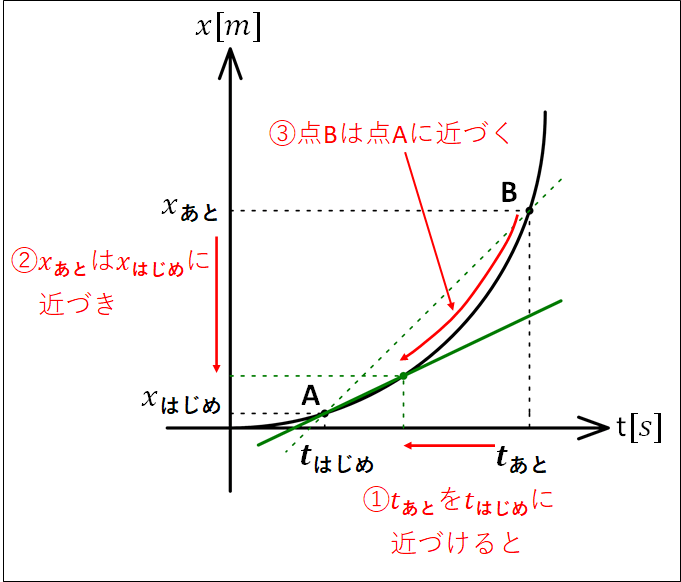
↓
ここで、\(t_{\bf{あと}}\)を限りなく\(t_{\bf{はじめ}}\)に近づけると、その傾きが瞬間の速度となる。
(点\(A\)における接線の傾きが瞬間の速度)
↓
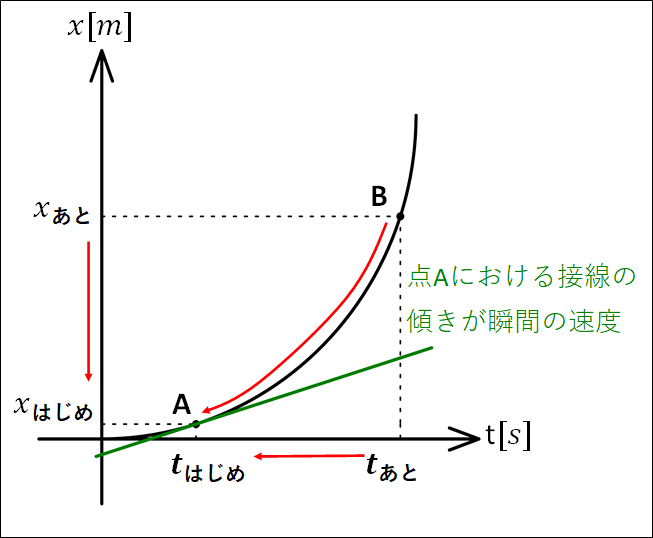
\(\textcolor{red}{\bf{○ポイント}}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・平均の速度}\\\\x-t{\bf{グラフのはじめの点とあとの点を結んだ直線の傾き}}}}\end{eqnarray}\)
\(\begin{eqnarray}\textcolor{red}{{\bf{・瞬間の速度}\\\\x-t{\bf{グラフのある点における直線の傾き}}}}\end{eqnarray}\)
※補足
数学的に…
平均の速度は
\(\displaystyle{\begin{eqnarray}\bar{v}&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}}{t_{\bf{あと}}-t_{\bf{はじめ}}}\\\\&=&\frac{\Delta{x}}{\Delta{t}}\end{eqnarray}}\)
ここで、\(t_{\bf{あと}}\)を\(t_{\bf{はじめ}}\)に限りなく近づけると、\(\Delta{t}\)は限りなく\(0\)に近づきます。
\(\Delta{t}\)を限りなく近づけるという記号である\(\displaystyle{\lim_{\Delta{t}\to0}}\)を用いると、瞬間の速度\(v\)は
\(\displaystyle{\begin{eqnarray}v&=&\lim_{\Delta{t}\to0}\bar{v}\\\\&=&\lim_{\Delta{t}\to0}\frac{\Delta{x}}{\Delta{t}}\\\\&=&\frac{dx}{dt}\end{eqnarray}}\)
となります。
これは数学でいう微分の考え方で、位置\(x\)を時間\(t\)で微分したものが瞬間の速度であるという意味になります。
(位置\(x\)は時間\(t\)の関数)
記号の感覚的には、\(\Delta{t}\)を限りなく\(0\)に近づけたので、
\(\displaystyle{\frac{dx}{dt}=\frac{{\bf{限りなく小さい}}x{\bf{のあと-はじめ}}}{{\bf{限りなく小さい}}t{\bf{のあと-はじめ}}}}\)
になります。
微分についてはこちらも参考にしてください
→微分係数と導関数
→微分法とその応用
4.加速度
物体が動いている方向に速度を加えていくと、物体はどんどん速くなります。
逆に、物体が動いている方向と逆向きに速度を加えていくと、物体はどんどん遅くなります。
\(\textcolor{red}{\bf{加速度}}\)とは、上記の速度を加えていくことに関して、単位時間(\(1\)秒間)あたりにどれだけ速度を加えるかを表す量となります。
また、加速度も向き(符合)と大きさをもつベクトルとなります。
平均の加速度\(\bar{a}\)の定義は以下のようになります。
(\(a\)は\(acceleration\)(加速度)の頭文字)
\(\displaystyle{\textcolor{green}{\bar{a}[m/s^2]=\frac{v_{\bf{あと}}-v_{\bf{はじめ}}[m/s]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}}}\)
となり、平均の速度の定義式の分子が位置\(x\)から速度\(v\)に変わったものになります。
分子は速度のあと-はじめ、分母は時間のあと-はじめとなります。
また、あと-はじめ(変化量)という意味の記号\(\Delta\)(デルタ)を用いて
\(\displaystyle{\bar{a}[m/s^2]=\frac{\Delta{v}[m/s]}{\Delta{t}[s]}}\)
とも表せます。
単位は、
\(m/s÷s=m/s^2\)(メートル毎秒毎秒)
となります。
瞬間の加速度は、瞬間の速度を考えたときと同様にして、時間の変化量\(\Delta{t}\)を(0)に近づけ
\(\displaystyle{a[m/s]=\lim_{\Delta{t}\to0}\frac{\Delta{v}[m/s]}{\Delta{t}[s]}=\frac{dv}{dt}[m/s^2]}\)
です。
速度\(v\)が位置\(x\)と時間\(t\)の関係を表す\(x-t\)グラフの傾きであったことと同様に、\(\textcolor{red}{\bf{加速度}}\)\(\textcolor{red}{a}\)\(\textcolor{red}{\bf{は速度}}\)\(\textcolor{red}{v}\)\(\textcolor{red}{\bf{と時間}}\)\(\textcolor{red}{t}\)\(\textcolor{red}{\bf{の関係を表す}}\)\(\textcolor{red}{v-t}\)\(\textcolor{red}{\bf{グラフの傾きを表しています}}\)
5.まとめ
\(\bf{[変位の定義]}\)
変位:
\(\textcolor{green}{\Delta{x}[m]=x_{\bf{あと}}-x_{\bf{はじめ}}}\)
(\(x\)軸上の運動の場合)
\(\bf{[速度の定義]}\)
○平均の速度
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\bar{v}[m/s]&=&\frac{x_{\bf{あと}}-x_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{x}[m]}{\Delta{t}[s]}\end{eqnarray}}}\)
\(x-t\)グラフのあととはじめの点を結んだ直線の傾きを表す。
○瞬間の速度
\(\displaystyle{v[m/s]=\frac{dx}{dt}[m/s]}\)
\(x-t\)グラフのある点の接線の傾きを表す。
\(\bf{[加速度の定義]}\)
○平均の加速度
\(\displaystyle{\textcolor{green}{\begin{eqnarray}\bar{a}[m/s^2]&=&\frac{v_{\bf{あと}}-v_{\bf{はじめ}}[m]}{t_{\bf{あと}}-t_{\bf{はじめ}}[s]}\\\\&=&\frac{\Delta{v}[m/s]}{\Delta{t}[s]}\end{eqnarray}}}\)
\(v-t\)グラフのあととはじめの点を結んだ直線の傾きを表す。
○瞬間の加速度
\(\displaystyle{a[m/s^2]=\frac{dv}{dt}[m/s^2]}\)
\(v-t\)グラフのある点の接線の傾きを表す。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

関連記事
→変位・速度・加速度(補足解説と練習問題)

