投稿日:
【高校物理】よく使う積分の考え方と微積公式まとめ【高校数学】【微分】【積分】
\(\require{color}\)
\(\require{cancel}\)
こちらは、\(dx\)を微小区間、\(\displaystyle{\int_a^b}\)を\(a\)から\(b\)まで滑らかに足し合わせると考えた際の、積分計算の考え方について解説しています。
また、微分公式と積分公式をまとめています。
微分・積分に関する記事は、こちらも参考にしてください
→微分係数と導関数
→積分法
→様々な関数
→極限
→微分法とその応用
→積分法の応用
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.よく使う積分の考え方
1-1.面積
「積分法の応用」では区分求積法を扱いました。
区分求積法では、区間を\(n\)等分して、この\(n\)を限りなく大きくしていくと分割幅は限りなく小さくなってくので、着目している長方形は限りなく細くなっていきます。
長方形が細くなっていくと、長方形の面積とグラフとの隙間が無くなっていき、細長い長方形(ほぼ線)を全て足し合わせると、注目している部分の面積になるというものでした。
これとほぼ同じような考え方で、積分記号を捉えることがあります。
\(y=f(x)\)のグラフについて、\(x\)座標が\(x\)である部分を考えます。
この点における\(y\)座標の値は\(f(x)\)となります。
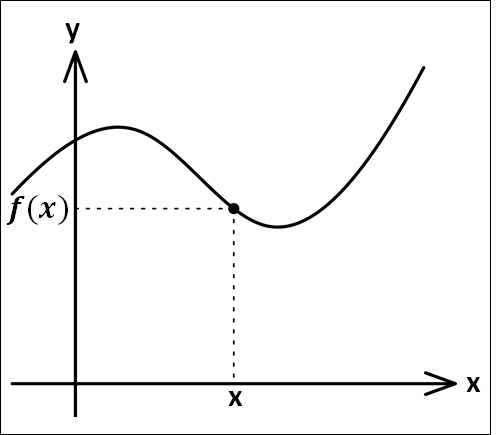
この\(x\)座標部分について、限りなく小さな幅を\(dx\)とします。
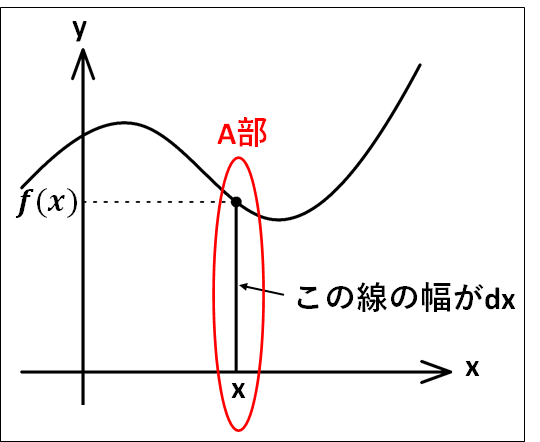
上図A部の横幅を拡大すると、下図のようになります。
(スケールは正しくないですが、イメージはこのような感じです)
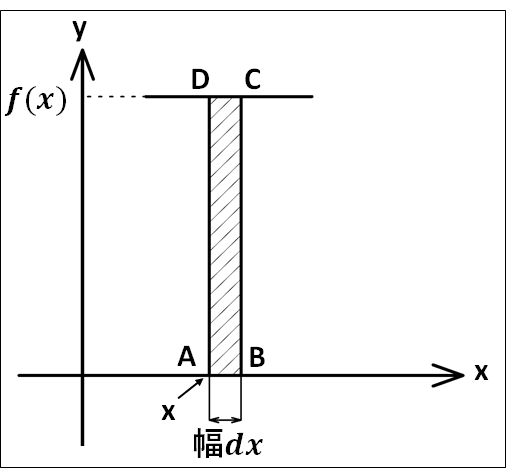
\(y=f(x)\)は曲線ですが、幅\(dx\)は微小なのでこの部分を拡大すると、上図\(DC\)は直線であるとみなせます。
よって、上図の\(ABCD\)は長方形とみなせ、この微小な面積は縦幅が\(f(x)\)、横幅が\(dx\)なので\(f(x)dx\)となります。
この長方形を、\(x\)の値を\(a\to{b}\)へと変化させなめらかに足し合わせていくと、\(y=f(x)\)のグラフと\(x\)軸、\(x=a , x=b\)で囲まれた部分の面積となります。
この面積を\(S\)とします。
(例えば、\(x=a\)のときの長方形の面積は、\(f(a)dx\)となる。これを\(x\)を\(a\to{b}\)へと変化させていった際の各長方形の面積を足したものが\(S)\)
ここで積分の記号\(\displaystyle{\int_a^b}\)を、\(x\)を\(a\)から\(b\)まで変化させ滑らかに足すという意味だと捉えると、面積\(S\)は
\(\displaystyle{S=\int_a^b{f(x)}dx}\)
と表せます。
上式は、微小な長方形の面積\(f(x)dx\)において、\(x\)を\(a\to{b}\)まで滑らかに足していった和が\(S\)という意味になります。
\(x\)の値を\(a\to{b}\)に変化させていくと、長方形の縦の長さ\(f(x)\)も\(f(a)\to{f(b)}\)へと滑らかに変化していきます。
イメージは下図のようになります。
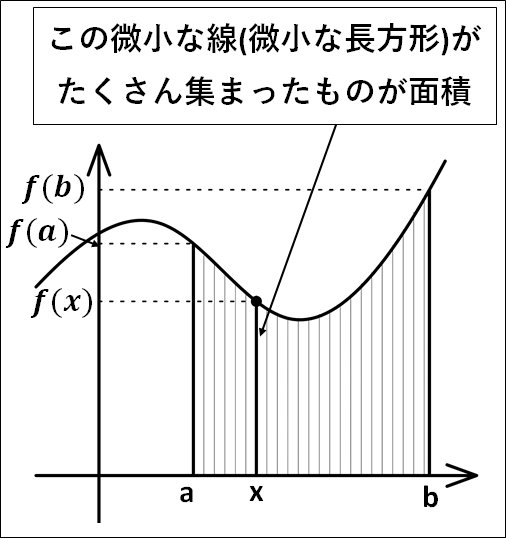
また、同様にして2つの関数\(y=f(x)\)と\(y=g(x)\)を考えると下図のようになります。
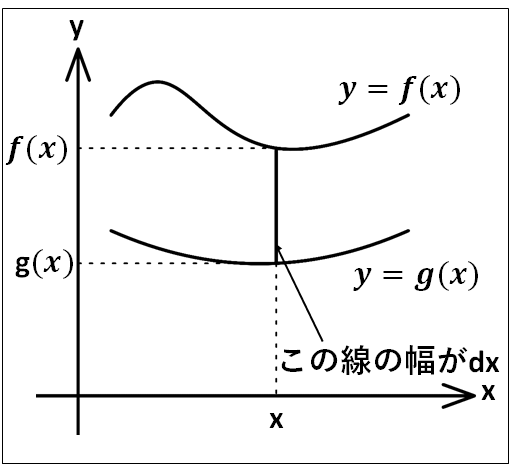
上記と同様にして、微小幅\(dx\)を考え、注目している部分を拡大すると、下図のようになります。
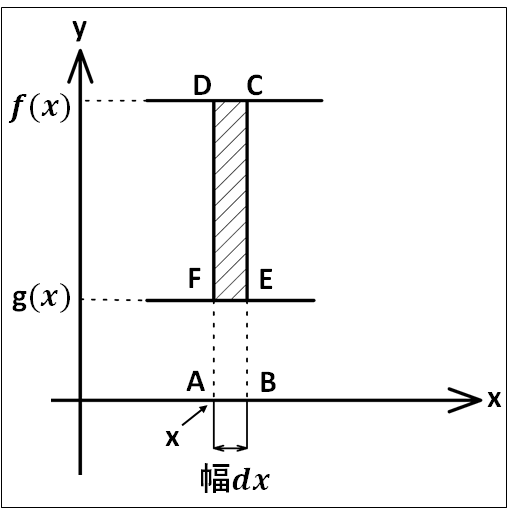
この微小長方形の\(y=f(x)\)と\(y=g(x)\)の間の面積は上図の斜線部となります。
この面積は、長方形\(ABCD\)から\(ABEF\)を引いた、\(FECD\)となります。
長方形\(ABCD\)の面積は横幅が\(dx\)、縦幅が\(f(x)\)なので
\(f(x)dx\)
長方形\(ABEF\)の面積は横幅が\(dx\)、縦幅が\(g(x)\)なので
\(g(x)dx\)
よって、微小長方形\(FECD\)の面積は、\(ABCD\)から\(ABEF\)を引いて
\(f(x)dx-g(x)dx=\left\{f(x)-g(x)\right\}dx\)
となります。
ここで、上記と同様にして\(\displaystyle{\int_a^b}\)を\(x\)の値を\(a\to{b}\)まで変化させて滑らかに足すという意味であると捉えると、\(y=f(x) , y=g(x) , x=a , x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_a^b\left\{f(x)-g(x)\right\}dx}\)
となります。
上式の意味は、微小な長方形\(\left\{f(x)-g(x)\right\}dx\)の\(x\)の値を\(a\to{b}\)まで変化させ足し合わせた和が\(S\)であるという意味になります。
1-2.体積
こちらも面積と同様に考えて、ある点における微小体積を考えてそれを足すというふうに考えます。
状況を下図のように設定します。
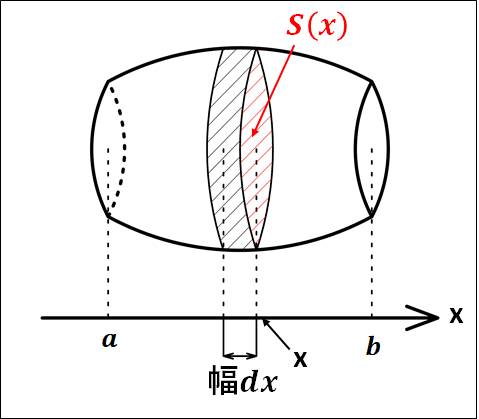
上図では、幅\(dx\)は分かりやすいように大きくしていますが、実際には限りなく小さい微小な幅であると思ってください。
上図のように\(x\)軸上に、点\(x\)を通り\(x\)軸と垂直な面で切った立体の断面積を\(S(x)\)とします。
この断面積\(S(x)\)と、限りなく小さな微小幅\(dx\)を考えると、この部分の微小体積は(面積×厚み)で\(S(x)dx\)となります。
この微小体積を\(x=a\)から\(x=b\)までなめらかに足し合わせていったものが、この立体の体積\(V\)となるので、面積のときと同様に\(\displaystyle{\int_a^b}\)を、\(x\)の値を\(a\to{b}\)まで変化させて滑らかに足すという意味であると捉えると、体積\(V\)は
\(\displaystyle{V=\int_a^b{S(x)}dx}\)
となります。
以上のように微小な幅を\(dx\)として、その際の微小面積あるいは微小体積を考えます。
そして、\(\displaystyle{\int_a^b}\)を\(x\)を\(a\)から\(b\)まで変化させて考えている微小面積あるいは微小体積をなめらかに足し合わせていくという意味だと捉えて立式する考え方もあります。
高校物理ではあまり扱いませんが、材料力学の教科書などにはこのような考え方で計算を進めているイメージがあります。
2.微分の公式まとめ
以下に、微分に関する公式をまとめておきます。
\(\underline{\bf{導関数の定義}}\)
\(\displaystyle{\begin{eqnarray}f'(x)&=&\lim_{h\to0}\frac{f(x+h)-f(x)}{(x+h)-x}\\\\&=&\lim_{h\to0}\frac{f(x+h)-f(x)}{h}\end{eqnarray}}\)
\(\Delta{x}=(x+h)-x\)、\(\Delta{y}=f(x+h)-f(x)\)とすると
\(\displaystyle{f'(x)=\lim_{h\to0}\frac{\Delta{y}}{\Delta{x}}}\)
\(\underline{{\bf{導関数の性質}}}\)
関数\(f(x),g(x)\)がともに微分可能であるとき
○定数倍
\(\displaystyle{\left\{kf(x)\right\}’=kf'(x) (kは定数)}\)
○和
\(\displaystyle{\left\{f(x)+g(x)\right\}’=f'(x)+g'(x)}\)
○差
\(\displaystyle{\left\{f(x)-g(x)\right\}’=f'(x)-g'(x)}\)
\(\underline{{x^a}{\bf{の微分}}}\)
\(a\)が実数のとき
\(\displaystyle{(x^a)’=ax^{a-1}}\)
\(\underline{{\bf{積の微分}}}\)
\(\displaystyle{\left\{f(x)g(x)\right\}’=f'(x)g(x)+f(x)g'(x)}\)
\(\underline{{\bf{商の微分}}}\)
\(\displaystyle{\left\{\frac{1}{g(x)}\right\}’=-\frac{g'(x)}{\left\{g(x)\right\}^2}}\)
\(\displaystyle{\left\{\frac{f(x)}{g(x)}\right\}’=\frac{f'(x)g(x)-f(x)g'(x)}{\left\{g(x)\right\}^2}}\)
\(\underline{{\bf{合成関数の微分}}}\)
\(\displaystyle{\frac{dy}{dx}=\frac{dy}{du}・\frac{du}{dx}}\)
\(\underline{{\bf{逆関数の微分}}}\)
\(\displaystyle{\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}}\)
\(\underline{{\bf{三角関数の微分}}}\)
\(\displaystyle{(\sin{x})’=\cos{x}}\)
\(\displaystyle{(\cos{x})’=-\sin{x}}\)
\(\displaystyle{(\tan{x})’=\frac{1}{\cos^2{x}}}\)
\(\underline{{\bf{対数関数の微分}}}\)
○\(e\)の定義
\(\displaystyle{\lim_{k\to0}(1+k)^{\frac{1}{k}}=e}\)
または
\(\displaystyle{\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n}\)
○対数関数の微分
\(\displaystyle{(\log_a{x})’=\frac{1}{x\log{a}}}\)
\(\displaystyle{(\log{x})’=\frac{1}{x}}\)
\(\displaystyle{(\log|x|)’=\frac{1}{x}}\)
\(\displaystyle{(\log_a{|x|})’=\frac{1}{x\log{a}}}\)
\(\underline{{\bf{指数関数の微分}}}\)
\(\displaystyle{(e^x)’=a^x\log{a}}\)
\(\displaystyle{(e^x)’=e^x}\)
\(\underline{{\bf{曲線の媒介変数表示と導関数}}}\)
\(x=f(t),y=g(t)\)のとき
\(\displaystyle{\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{g'(t)}{f'(t)}}\)
3.積分の公式まとめ
3-1.不定積分
以下に、不定積分に関する公式をまとめておきます。
\(\underline{{f(x)}{\bf{の不定積分}}}\)
\(\displaystyle{F'(x)=f(x)}\)のとき、\(f(x)\)の不定積分は
\(\displaystyle{\int{f(x)}dx=F(x)+C (Cは積分定数)}\)
\(\underline{{x^{\alpha}}{\bf{の不定積分}}}\)
\(\displaystyle{\int{x^{\alpha}}dx=\frac{1}{\alpha+1}x^{\alpha+1}+C (\alpha\neq-1)}\)
\(\displaystyle{\int{\frac{1}{x}}dx=\log|x|+C}\)
\(\underline{{\bf{不定積分の性質}}}\)
○定数倍
\(\displaystyle{\int{kf(x)}dx=k\int{f(x)}dx (kは定数)}\)
○和
\(\displaystyle{\int\left\{f(x)+g(x)\right\}dx=\int{f(x)}dx+\int{g(x)}dx}\)
○差
\(\displaystyle{\int{\left\{f(x)-g(x)\right\}}dx=\int{f(x)}dx-\int{g(x)}dx}\)
\(\underline{{\bf{三角関数の不定積分}}}\)
\(\displaystyle{\int\sin{x}dx=-\cos{x}+C}\)
\(\displaystyle{\int\cos{x}dx=\sin{x}+C}\)
\(\displaystyle{\int{\frac{1}{\cos^2{x}}}dx=\tan{x}+C}\)
\(\underline{{\bf{指数関数の不定積分}}}\)
\(\displaystyle{\int{e^x}dx=e^x+C}\)
\(\displaystyle{\int{a^x}dx=\frac{a^x}{\log{a}}+C}\)
\(\underline{{\bf{置換積分}}}\)
\(F'(x)=f(x) , a\neq0\)のとき
\(\displaystyle{\int{f(ax+b)}dx=\frac{1}{a}F(ax+b)+C}\)
\(\displaystyle{\int{f(x)}dx=\int{f(g(t))・g'(t)}dt (x=g(t))}\)
\(\displaystyle{\int{f(g(x))・g'(x)}dx=\int{f(u)}du (g(x)=u)}\)
\(\displaystyle{\int{\frac{g'(x)}{g(x)}}dx=\log|g(x)|+C}\)
\(\underline{{\bf{部分積分}}}\)
\(\displaystyle{\int{f(x)g'(x)}dx=f(x)g(x)-\int{f'(x)g(x)}dx}\)
3-2.定積分
以下に、定積分に関する公式をまとめておきます。
\(\underline{{\bf{定積分}}}\)
区間\([a,b]\)で連続な関数\(f(x)\)の原始関数の1つを\(F(x)\)とすると
\(\displaystyle{\int_a^b{f(x)}dx=\left[F(x)\right]_a^b=F(b)-F(a)}\)
\(\underline{{\bf{定積分の性質}}}\)
○定数倍
\(\displaystyle{\int_a^b{kf(x)}dx=k\int_a^b{f(x)}dx (kは定数)}\)
○和
\(\displaystyle{\int_a^b{\left\{f(x)+g(x)\right\}}dx=\int_a^b{f(x)}dx+\int_a^b{g(x)}dx}\)
○差
\(\displaystyle{\int_a^b{\left\{f(x)-g(x)\right\}}dx=\int_a^b{f(x)}dx-\int_a^b{g(x)}dx}\)
○積分区間に関するもの
\(\displaystyle{\int_a^a{f(x)}dx=0}\)
\(\displaystyle{\int_b^a{f(x)}dx=-\int_a^b{f(x)}dx}\)
\(\displaystyle{\int_a^b{f(x)}dx=\int_a^c{f(x)}dx+\int_c^b{f(x)}dx}\)
\(\underline{{\bf{定積分の置換積分}}}\)
\(x=g(t)\)とおくとき、\(a=g(\alpha),b=g(\beta)\)ならば
\(\displaystyle{\int_a^b{f(x)}dx=\int_{\alpha}^{\beta}{f(g(t))・g'(t)}dt}\)
積分変数が\(x\)から\(t\)になるので、\(x:a\to{b}\)のとき\(t:\alpha\to{\beta}\)のように積分区間の変更が必要
置換積分において特に、
☆\(\sqrt{a^2-x^2}\)の形では、\(x=a\sin{\theta}\)とおいてみる
☆\(\displaystyle{\frac{1}{x^2+a^2} (a\gt0)}\)の形では、\(x=a\tan{\theta}\)とおいてみる
\(\underline{{\bf{偶関数と奇関数の定積分}}}\)
○偶関数\(f(x)\)について
\(\displaystyle{\int_{-a}^a{f(x)}dx=2\int_0^a{f(x)}dx}\)
○奇関数\(f(x)\)について
\(\displaystyle{\int_{-a}^a{f(x)}dx=0}\)
\(\underline{{\bf{定積分の部分積分}}}\)
\(\displaystyle{\int_a^b{f(x)g'(x)}dx=\left[f(x)g(x)\right]_a^b-\int_a^b{f'(x)g(x)}dx}\)
\(\underline{{\bf{区分求積法と定積分}}}\)
\(\displaystyle{\lim_{n\to\infty}\sum_{k=1}^n{f(x_k)\Delta{x}}=\int_a^b{f(x)}dx}\)
ただし、\(\displaystyle{\Delta{x}=\frac{b-a}{n} , x_k=a+k\Delta{x}}\)
特に、\(a=0,b=1\)のとき
\(\displaystyle{\lim_{h\to0}\frac{1}{n}\sum_{k=1}^n{f\left(\frac{k}{n}\right)}=\int_0^1{f(x)}dx}\)
ただし、\(\displaystyle{\Delta{x}=\frac{1}{n} , x_k=\frac{k}{n}}\)
\(\underline{{\bf{面積}}}\)
○区間\([a,b]\)で常に\(f(x)\ge0\)のとき、曲線\(y=f(x)\)と\(x\)軸および2直線\(x=a,x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_a^b{f(x)}dx}\)
○区間\(a{\le}x{\le}b\)で常に\(f(x)\ge{g(x)}\)のとき、2つの曲線\(y=f(x),y=g(x)\)と2直線\(x=a,x=b\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_a^b{\left\{f(x)-g(x)\right\}}dx}\)
○区間\(c{\le}x{\le}d\)で常に\(g(y)\ge0\)のとき、曲線\(x=g(y)\)と\(y\)軸および2直線\(y=c\)と\(y=d\)で囲まれた部分の面積\(S\)は
\(\displaystyle{S=\int_c^d{g(y)}dy}\)
また、面積については微小幅\(dx\)を考えその部分における微小面積\(f(x)dx\)を\(\displaystyle{\int_a^b}\)で\(x\)を\(a\)から\(b\)まで滑らかに足し合わせるという式が
\(\displaystyle{\int_a^b{f(x)}dx}\)
であると考えることもできます。
\(\underline{{\bf{体積}}}\)
○体積
断面積を\(S(x)\)とすると、\(x\)座標が\(a\)から\(b\)までの立体の体積\(V\)は
\(\displaystyle{V=\int_a^b{S(x)}dx} (a\lt{b})\)
○\(x\)軸周りの回転体の体積
\(x\)座標が\(a\)から\(b\)までの\(x\)軸周りの回転体の体積\(V\)は
\(\displaystyle{V=\pi\int_a^b{\left\{f(x)\right\}^2}dx=\pi\int_a^b{y^2}dx (a\lt{b})}\)
○\(y\)軸周りの回転体の体積
\(y\)座標が\(c\)から\(d\)までの\(y\)軸周りの回転体の体積\(V\)は
\(\displaystyle{V=\pi\int_a^b{\left\{g(y)\right\}^2}dx=\pi\int_a^b{x^2}dx (c\lt{d})}\)
また、体積については微小幅\(dx\)を考えその部分における微小体積\(S(x)dx\)を\(\displaystyle{\int_a^b}\)で\(x\)を\(a\)から\(b\)まで滑らかに足し合わせるという式が
\(\displaystyle{\int_a^b{S(x)}dx}\)
であると考えることもできます。
今回は以上となりますが、微分・積分の公式は丸暗記するというよりも、どのように用いるかを知るということが大切であると思います。
特に、置換積分や部分積分については何を置換するかや、何を微分したものとおくか、または何を積分したものとおくか、ということが重要になってくるので、どのように工夫すれば計算ができるかということを見抜くことが必要です。
なので、公式をどのように用いるかを練習し、その過程で経験を身につけ置換積分や部分積分を行えるようにすることが大切だと思います。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


