投稿日:
【高校物理】様々な関数(分数関数/無理関数/逆関数/合成関数)【高校数学】【分数関数】【無理関数】【逆関数】【合成関数】
\(\require{color}\)
\(\require{cancel}\)
分数関数や無理関数などの基本的な部分を解説していきます。
また、微分や積分において、逆関数や合成関数というものも扱うので、この記事でこれらの解説もしていきます。
微分・積分に関する記事は、こちらも参考にしてください
→微分係数と導関数
→積分法
→極限
→微分法とその応用
→積分法の応用
→よく使う積分の考え方と微積公式まとめ
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog

目次
1.分数関数
分数関数とは、\(\displaystyle{y=\frac{1}{x}}\)のように、\(x\)の分数式で表される関数のことです。
\(\displaystyle{y=\frac{k}{x} (k\neq0)}\)のとき、定義域は\(x\neq0\)、値域は\(y\neq0\)となります。
また、漸近線(グラフが近づく線)は\(x=0\)、\(y=0\)となります。
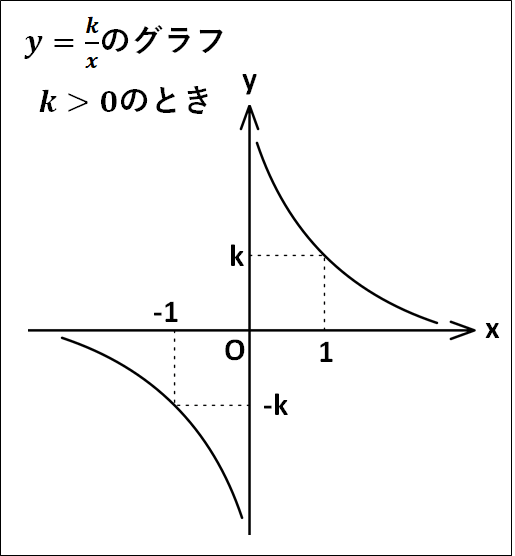
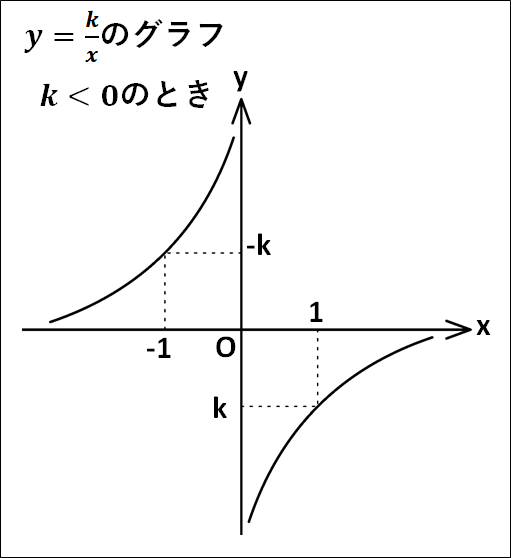
\(\displaystyle{y=\frac{k}{x}}\)において、
\(k=0\)だと関数は\(y=0\)となってしまい変数\(x\)は無関係になってしまうので分数関数とはなりません。
したがって、\(k\)は\(k\neq0\)である必要があります。
また、分母に\(0\)をとることはできないので\(x\neq0\)となり、\(k\neq0\)かつ\(x\neq0\)の条件では、\(\displaystyle{\frac{k}{x}}\)は\(0\)とはならないので、
\(\displaystyle{y=\frac{k}{x}\neq0}\)
となります。
漸近線については、
\(x\)を正の方向に大きくしていった場合、\(\displaystyle{\frac{k}{x}}\)の分母が大きくなっていくと\(\displaystyle{\frac{k}{x}}\)全体としては小さくなっていき、\(\displaystyle{y=\frac{k}{x}}\)は\(0\)に近づきます。
これは、\(x\)を負の方向に大きくしていった場合についても同様となります。
次に、\(k\gt{0}\)の場合について、\(x\)を\(0\)に近づけていくことを考えます。
\(x\)が正で、\(0\)に近づけた場合、例えば\(x=+0.001\)などの場合、
\(\displaystyle{\begin{eqnarray}y&=&\frac{k}{0.001}\\\\&=&\frac{k}{\frac{1}{1000}}\\\\&=&1000×k\end{eqnarray}}\)
のように、分母の値が小さいほど\(\displaystyle{\frac{k}{x}}\)は大きくなっていきます。
よって、\(x\)が正の値で\(0\)に近づくほど\(\displaystyle{\frac{k}{x}}\)は限りなく正の方向に大きくなっていきます。
\(x\)が負の値で\(0\)に近づいていくとき、例えば\(-0.001\)などの場合について考えると、
\(\displaystyle{\begin{eqnarray}y&=&\frac{k}{-0.001}\\\\&=&\frac{k}{-\frac{1}{1000}}\\\\&=&-1000×k\end{eqnarray}}\)
となるので、\(x\)が負の値で\(0\)に近づくほど\(\displaystyle{\frac{k}{x}}\)は限りなく負の方向に大きくなっていきます。
これは、\(k\lt{0}\)の場合についても同様に考えることができますが、\(x\)が正の値で\(0\)に近づく場合、\(x\gt0\)で\(k\lt0\)なので、\(\displaystyle{\frac{k}{x}}\)は負の方向に限りなく大きくなっていき、\(x\)が負の値で\(0\)に限りなく近づいていくときには、\(x\lt0\)で\(k\lt0\)なので\(\displaystyle{\frac{k}{x}}\)は正の方向に限りなく大きくなっていきます。
また、\(x=1\)のとき
\(\displaystyle{y=\frac{k}{1}=k}\)
となり、\(x=-1\)のとき
\(\displaystyle{\frac{k}{-1}=-k}\)
となり、グラフ概形に記したような値になりますが、\(k\lt0\)のときには\(k\lt0\)および\(-k\gt0\)となることに注意してください。
(\(k\)が負のとき、\(-k\)は負×負で正となる)
\(\displaystyle{\underline{y=\frac{k}{x-\textcolor{red}{p}}+\textcolor{blue}{q}\bf{のグラフ}}}\)
\(\displaystyle{y=\frac{k}{x-\textcolor{red}{p}}+\textcolor{blue}{q}}\)のグラフは\(y=a(x-\textcolor{red}{p})+\textcolor{blue}{q}\)のグラフが\(y=ax\)のグラフを\(x\)軸方向に\(+\textcolor{red}{p}\)、\(y\)軸方向に\(+\textcolor{blue}{q}\)だけ平行移動したものと同様に、\(\displaystyle{y=\frac{k}{x}}\)のグラフを\(x\)軸方向に\(+\textcolor{red}{p}\)、\(y\)軸方向に\(+\textcolor{blue}{q}\)だけ平行移動したものとなります。
漸近線も\(x\)軸方向に\(+\textcolor{red}{p}\)、\(y\)軸方向に\(+\textcolor{blue}{q}\)だけ平行移動されているので、このグラフの漸近線は\(x=\textcolor{red}{p}\)、\(y=\textcolor{blue}{q}\)となります。
定義域は\(x{\neq}\textcolor{red}{p}\)、値域は\(y{\neq}\textcolor{blue}{q}\)となります。
例) \(\displaystyle{y~\frac{3}{x-2}+2}\)のグラフ
上記の事柄から、\(\displaystyle{y~\frac{3}{x-2}+2}\)のグラフは\(\displaystyle{y=\frac{3}{x}}\)のグラフを\(x\)軸方向に\(+2\)、\(y\)軸方向に\(+2\)だけ平行移動したものとなります。
漸近線は\(x=2\)、\(y=2\)となりグラフ概形は下図のようになります。
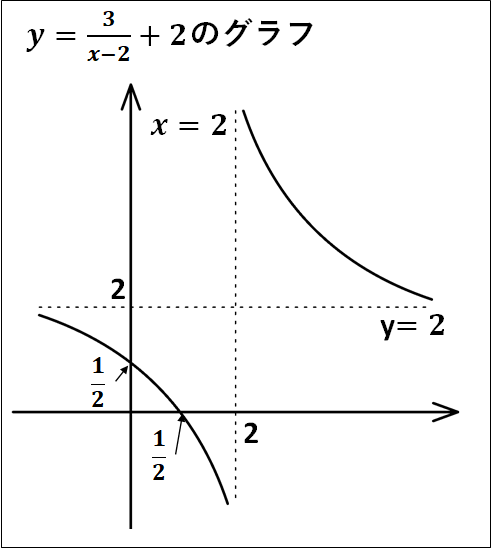
2.無理関数
無理関数とは\(y=\sqrt{x}\)のように根号の中に変数\(x\)を含む式で表された関数のことです。
定義域は根号の中が\(0\)以上となる実数\(x\)の値全体となります。
例えば、
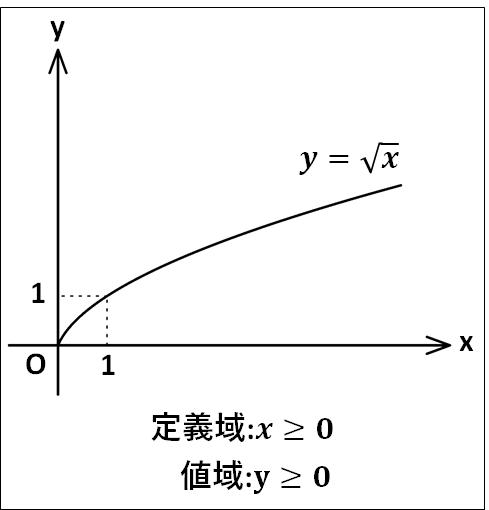
\(y=\sqrt{x} \cdots①\)
に関しては、定義域は根号の中が\(0\)以上、すなわち\(x\ge0\)であり、このとき値域は\(y\ge0\)となります。
\(①\)に関して、この式の両辺を2乗すると\(y^2=x\)となります。これは軸が\(x\)軸で頂点が原点である放物線となります。
また、\(y\ge0\)なのでグラフは次のようになります。
\(y=x^2\)と\(y^2=x\)を比較すると、\(x\)と\(y\)が入れ替わっているので、\(y^2=x\)のグラフは\(y=x^2\)のグラフを原点を中心に\(-90^\circ\)だけ回転させたものとなります。
(\(x\)軸→\(y\)軸に、\(y\)軸→\(x\)軸にしたもの)
ただし。定義域と値域には注意しなければなりません。
また、\(x=1\)のとき\(y=\sqrt{1}=1\)なので、このグラフは点\((1 , 1)\)を通ります。
他にも、\(y=-\sqrt{x}\)や\(y=\sqrt{-x}\)について考えてみます。
\(y=-\sqrt{x}\)について、定義域は根号の中が\(0\)以上なので\(x\ge0\)、値域は\(\sqrt{x}\ge0\)なので\(-\sqrt{x}\le0\)、すなわち\(y\le0\)となります。
以上から、グラフは下図のように\(y=\sqrt{x}\)のグラフとは\(x\)軸対称となります。
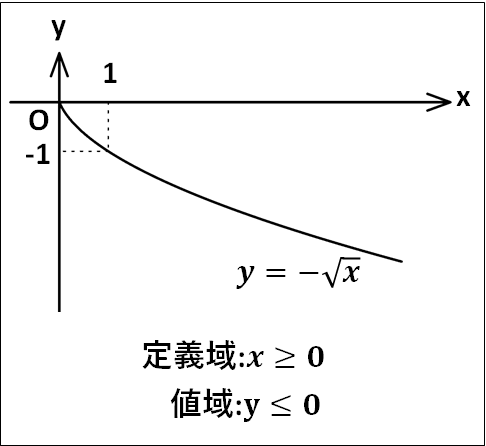
\(x=1\)のとき\(y=-\sqrt{1}=-1\)なので、このグラフは点\((1 , -1)\)を通ります。
\(y=\sqrt{-x}\)について、定義域は根号の中が\(0\)以上なので\(x\le0\)、値域は\(\sqrt{-x}\ge0\)なので\(y\ge0\)となります。
以上から、グラフは下図のように\(y=\sqrt{x}\)のグラフとは\(y\)軸対称となります。
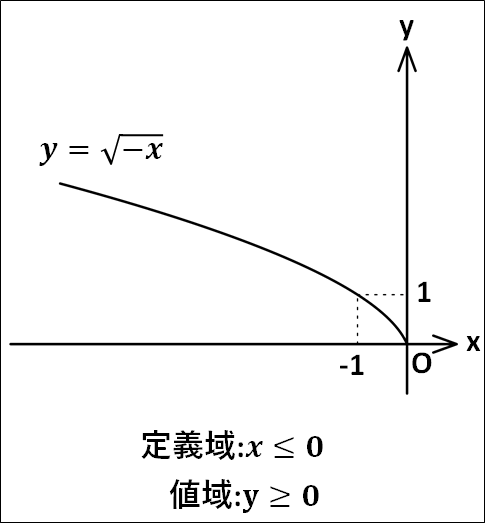
\(x=-1\)のとき\(y=\sqrt{-(-1)}=1\)なので、このグラフは点\((-1 , 1)\)を通ります。
以上のことを踏まえて、一般に\(y=\sqrt{ax}\)のグラフは以下のようになります。
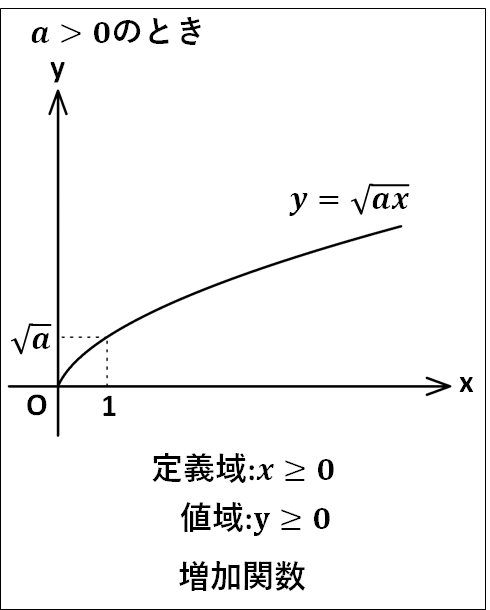
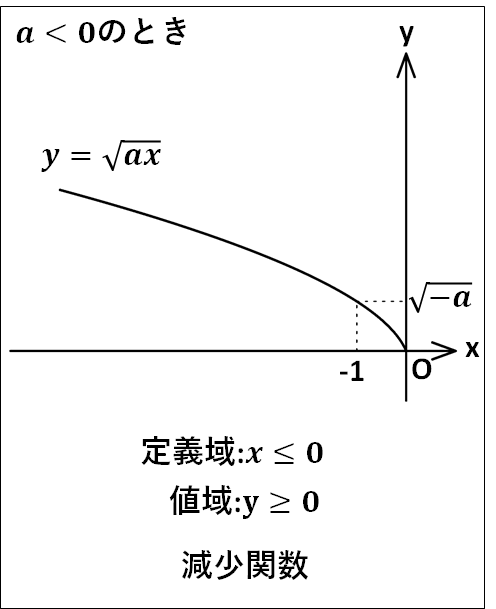
また、\(y=\sqrt{a(x-\textcolor{red}{p})}\)のグラフは、\(y=\sqrt{ax}\)のグラフを\(x\)軸方向に\(\textcolor{red}{p}\)だけ平行移動したもので、定義域は\(a(x-p)\ge0\)を満たす実数\(x\)の値全体で、値域は\(y\ge0\)となります。
例) \(y=\sqrt{2x-4}\)のグラフ
式変形をして、
\(y=\sqrt{2x-4}=\sqrt{2(x-2)}\)
よって、このグラフは\(y=\sqrt{2x}\)のグラフを\(x\)軸方向に\(+2\)平行移動したものとなります。
また、定義域は\(2(x-2)\ge0\)から\(x\ge2\)、値域は\(y\ge0\)となり、これらのことからグラフの概形は下図のようになります。
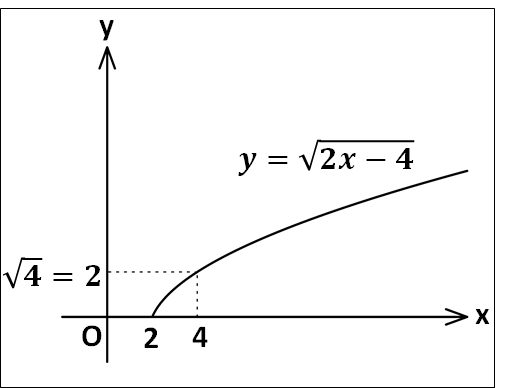
3.逆関数
関数\(y=f(x)\)が増加関数または減少関数のとき、値域の中の\(y\)の値を定めるとそれに対応して\(x\)の値がただ1つだけ定まります。
※例えば、増加関数\(y=2x (0\le{x}\le6)\)とすると、\(y=2\)のとき\(x=1\)とただ1つだけ定まる。
\(y=x^2\)だと、\(y=1\)のとき\(x=-1 , +1\)とただひとつには定まらない。
このことから、\(x\)は\(y\)の関数であるといえ、この関数を\(x=g(y)\)で表します。
この変数\(y\)を\(x\)に書き直した関数\(g(x)\)をもとの関数\(f(x)\)の逆関数といい\(f^{-1}(x)\)で表します。
(\(f^{-1}\)は「エフインバース」と呼ぶ)
また、\(\textcolor{red}{\bf{もとの}}\)\(\textcolor{red}{\bf{関数}}\)\(\textcolor{red}{\bf{と}}\)\(\textcolor{red}{\bf{その}}\)\(\textcolor{red}{\bf{逆関数}}\)\(\textcolor{red}{\bf{では、}}\)\(\textcolor{red}{\bf{定義域}}\)\(\textcolor{red}{\bf{と}}\)\(\textcolor{red}{\bf{値域}}\)\(\textcolor{red}{\bf{が}}\)\(\textcolor{red}{\bf{入れ替わります。}}\)
\(\underline{\bf{逆関数の求め方}}\)
\(f(x)\)の逆関数\(g(x)\)の求め方は、以下のようになります。
\(①\) \(y=f(x)\)を\(x\)について解いて、\(x=g(y)\)の形にする。
\(②\) \(x\)と\(y\)を入れ替えて、\(y=g(x)\)とし、逆関数\(g(x)\)の定義域はもとの関数\(f(x)\)の値域と同じにとる。
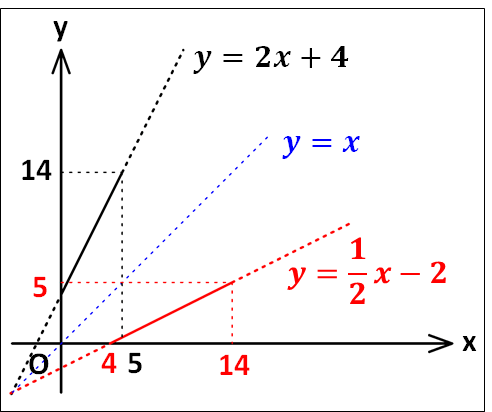
例1) \(f(x)=2x+4 (0\le{x}\le5)\)とするとき、\(y=f(x)\)の逆関数を求めてみます。
\(y=f(x)\)のグラフは増加関数であり、その値域は、
\(\displaystyle{\begin{eqnarray}&&0\le{x}\le5\\\\\Leftrightarrow&&0\le{2x}\le10\\\\\Leftrightarrow&&0\le{2x+4}\le14\\\\\Leftrightarrow&&4\le{y}\le14\end{eqnarray}}\)
より\(4\le{y}\le14\)となります。
\(y=2x+4\)を\(x\)について解くと、
\(\displaystyle{\begin{eqnarray}&&y=2x+4\\\Leftrightarrow&&y-4=2x\\\\\Leftrightarrow&&\frac{1}{2}y-2=x\end{eqnarray}}\)
この\(x\)と\(y\)を入れ替え、もとの関数の値域が定義域となるので、求める逆関数は、
\(\displaystyle{y=f^{-1}(x)=\frac{1}{2}x-2 (4\le{x}\le14)}\)
となります。
グラフの概形は下図のようになります。
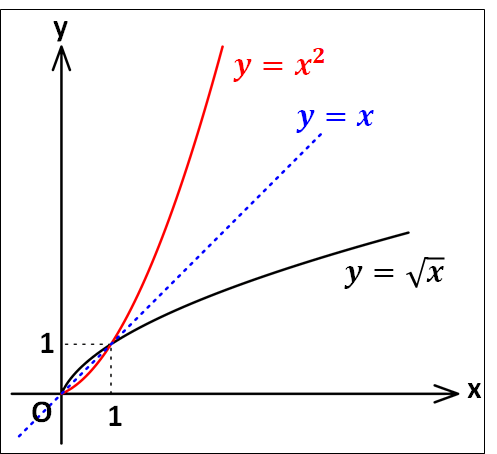
例2) \(y=\sqrt{x}\)の逆関数
\(y=\sqrt{x}\)の定義域と値域は\(x\ge0\)、\(y\ge0\)となります。
両辺を2乗して\(x\)について解くと
\(y^2=x\)
よって、\(x\)と\(y\)、また値域と定義域を入れ替えて、
\(y=x^2 (x\ge0 , y\ge0)\)
以上のことから、\(y=\sqrt{x}\)の逆関数は\(y=x^2 (x\ge0)\)となります。
グラフの概形は下図のようになります。
例3) \(y=x^2\)の逆関数
\(y=x^2\)を\(x\)について解くと、
\(x=\pm\sqrt{y}\)
このとき、\(y\)の値を定めても、\(x\)の値は1つに定まらない。
よって、\(y=x^2\)は\(\textcolor{red}{\bf{逆関数をもたない。}}\)
例4) \(y=x^2 (x\ge0)\)の逆関数
上記条件のとき、\(y=x^2 (x\ge0 , y\ge0)\)となります。
これを\(x\)について解くと、
\(x=\sqrt{y}\)
となります。
(\(x\ge0\)の条件から)
従って、定義域\((x\ge0)\)の範囲で\(y=x^2\)は逆関数をもち、その逆関数は、
\(y=\sqrt{x} (x\ge0 , y\ge0)\)
となります。
\(\underline{\bf{逆関数の性質}}\)
逆関数の性質に関して、次のことがいえます。
\(\underline{\bf{①}}\)
逆関数の定義から、関数\(f(x)\)が逆関数\(f^{-1}(x)\)をもつとき、
\(b=f(a)\Leftrightarrow{a}=f^{-1}(b)\)
が成り立ちます。
例)
関数\(f(x)\)が逆関数を持ち、\(3=f(6)\)のとき、\(6=f^{-1}(3)\)となる。
\(\underline{\bf{②}}\)
例のグラフ概形図にも少し描きましたが、
関数\(y=f(x)\)のグラフとその逆関数\(y=f^{-1}(x)\)のグラフは、直線\(y=x\)に関して対称となります。
上記性質は、
\(b=f(a)\Leftrightarrow{a=f^{-1}(b)}\)
から、点\(P(a , b)\)が関数\(y=f(x)\)上にあることと、点\(Q(b , a)\)が関数\(y=f^{-1}(x)\)上にあることとは同値となります。
そして、点\(P\)と点\(Q\)は直線\(y=x\)に関して対称となるので、関数\(y=f(x)\)のグラフとその逆関数\(y=f^{-1}(x)\)のグラフは直線\(y=x\)に関して対称となります。
4.合成関数
2つの関数\(f(x)\)、\(g(x)\)について、\(f(x)\)の値域が\(g(x)\)の定義域に含まれているとき、新しい関数\(g(f(x))\)を考えることができます。
この関数を\(f(x)\)と\(g(x)\)の合成関数といいます。
また、\(g(f(x))\)は\((g{\circ}f)(x)\)と書くこともあります。
例) \(f(x)=x+1\)、\(g(x)=x^2\)のとき、\((g{\circ}f)(x)\)と\((f{\circ}g)(x)\)を求めてみます。
\((g{\circ}f)(x) (=g(f(x)))\)について
\(f(x)\)の値域は実数全体であり、\(g(x)\)の定義域も実数全体なので、\(f(x)\)の値域は\(g(x)\)の定義域に含まれています。
このとき、
\(\displaystyle{\begin{eqnarray}(g{\circ}f)(x)&=&g(f(x))\\\\&=&g(x+1)\\\\&=&(x+1)^2\end{eqnarray}}\)
となります。
\((f{\circ}g)(x) (=f(g(x)))\)について
\(g(x)\)の値域は正の実数全体であり、\(f(x)\)の定義域は実数全体なので、\(g(x)\)の値域は\(f(x)\)の定義域に含まれています。
よって、
\(\displaystyle{\begin{eqnarray}(f{\circ}g)(x)&=&f(g(x))\\\\&=&f(x^2)\\\\&=&x^2+1\end{eqnarray}}\)
となります。
今回は以上となります。
よければ、ツイッターのフォローをよろしくお願いします。
Twitterアカウント→@roke_blog


